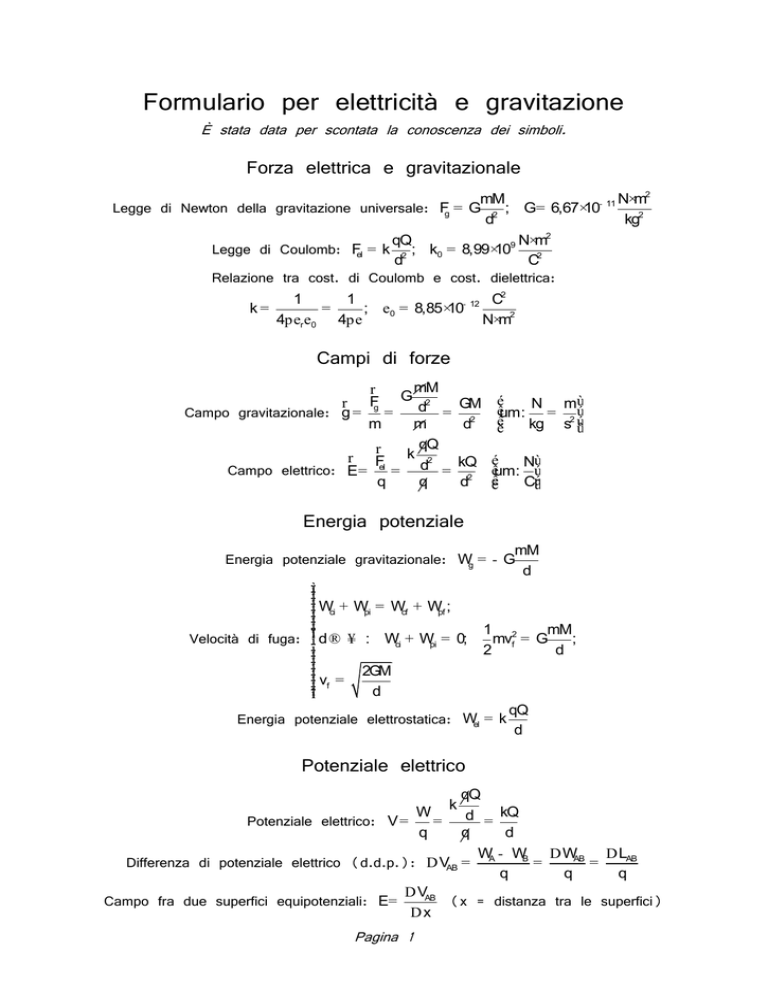
Formulario per elettricità e gravitazione
È stata data per scontata la conoscenza dei simboli.
Forza elettrica e gravitazionale
2
mM
- 11 N×m
Legge di Newton della gravitazione universale: Fg = G 2 ; G= 6,67×10
d
kg2
qQ
N×m2
Legge di Coulomb: Fel = k 2 ; k0 = 8,99×109 2
d
C
Relazione tra cost. di Coulomb e cost. dielettrica:
k=
1
1
C2
=
; e0 = 8,85×10- 12
4per e0 4pe
N×m2
Campi di forze
mM
r
r Fg G d2
Campo gravitazionale: g = =
=
m
m
qQ
r
r F k d2
Campo elettrico: E= el =
=
q
q
GM
d2
kQ
d2
é
N mù
êum: = 2 ú
êë
kg s ú
û
é
Nù
êum: ú
êë
Cú
û
Energia potenziale
mM
Energia potenziale gravitazionale: Wg = - G
d
ìï
ïï
ïï Wci + Wpi = Wcf + Wpf ;
ïï
1 2
mM
Velocità di fuga: ïí d ® ¥ : Wci + Wpi = 0;
mvf = G
;
ïï
2
d
ïï
2GM
ïï
ï vf =
d
ïî
qQ
Energia potenziale elettrostatica: Wel = k
d
Potenziale elettrico
qQ
d = kQ
q
d
W - WB D WAB D LAB
Differenza di potenziale elettrico (d.d.p.): D VAB = A
=
=
q
q
q
D VAB
Campo fra due superfici equipotenziali: E=
(x = distanza tra le superfici)
Dx
W
Potenziale elettrico: V =
=
q
Pagina 1
k
Flusso
Flusso elettrico: DF = E^ ×D A = E×cosq×D A
ìï
S Qint S Qsup
ïï F
+
sup.chiusa = 4p kQ =
ïï
e
2e
Teorema di Gauss: í
ïï
S Qint
ïï F sup.aperta =
e0
îï
Dipolo elettrico
r
r
Momento di dipolo: p = qd (d = lunghezza del dipolo)
Densità di carica
Densità lineare di carica: l =
q
Dl
q
DS
q
Densità volumica di carica: r =
DV
Densità superficiale di carica: s =
Teorema di Coulomb
Campo elettrico esterno al conduttore: E=
s
e
s
2e
F
s2
Pressione elettrostatica: pel = ^ =
D S 2e
Campo generato da una sfera omogenea carica elettricamente:
ìï
Q
ïï F sup.chiusa = S E×A = E×4p r 2 =
ï
e
í
ïï
Q
Q
=k 2
ïï E=
4per2
r
ïî
1 l
×
Campo generato da una distribuzione lineare di carica: E=
2pe r
s
Campo generato da una distribuzione superficiale di carica: E=
2e
s
s
Campo generato da un doppio strato elettrico: E= 2 =
2e e
Campo elettrico sul conduttore: E=
Capacità elettrica e condensatori
Pagina 2
ìï
Q
ïï C =
V
Capacità elettrica: ïí
ïï
S
ïï C = er e0
d
ïî
Capacità di un conduttore sferico: C= 4per
ïì Ceq = C1 + C2 + C3 ...
Condensatori collegati in parallelo: ïí
ïï Qtot = Ceq ×D V
î
ìï
1
ïï Ceq =
1
1
1
ïï
+
+
...
ïï
C1 C2 C3
Condensatori collegati in serie: í
ïï
æ1
1
1 ö
ïï
÷
ç
ïï D V = QççC + C + C ...÷
÷
÷
è 1
2
3 ø
ïî
ìï
ïï W = 1 QV
ïï
2
ïï
1
Energia in un condensatore: ïí W = CV2
ïï
2
ïï
2
ïï W = 1 Q
ïïî
2C
(Non garantisco assolutamente l’esattezza delle formule. Se trovi qualche errore, comunicamelo.)
Pagina 3












