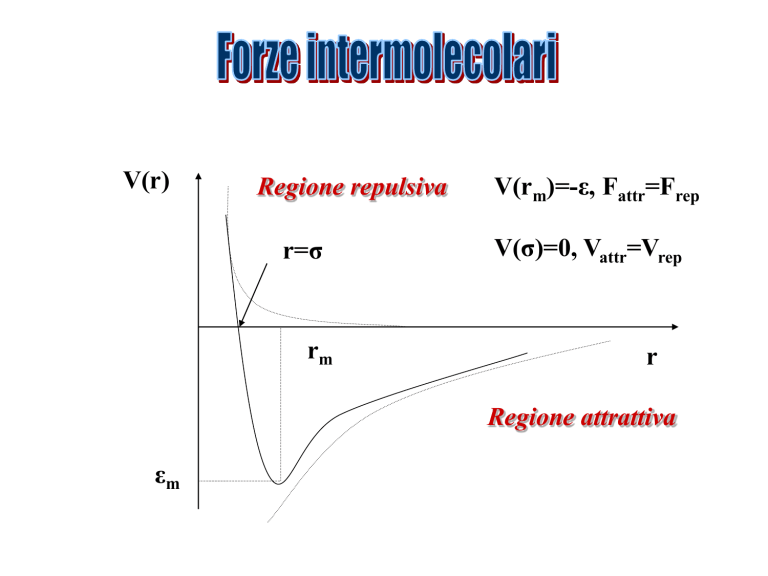
V(r)
Regione repulsiva
r=σ
rm
V(rm)=-ε, Fattr=Frep
V(σ)=0, Vattr=Vrep
r
Regione attrattiva
εm
Le interazioni a corto raggio sono dominate dalla repulsione
interelettronica e gli effetti sono necessariamente di tipo
quantistico (Principio di Pauli).
Sono le interazioni che danno luogo al concetto di ingombro
sterico.
V(r)
r
σ
Vrep(r≤σ)=∞
Vrep(r>σ)=0
r
r
σ=2r
Vatt=0
Una funzione che riproduce analiticamente i risultati dei
calcoli quantistici è:
V (R )
C
R
n
n 10,12
C = costante caratteristica della coppia di atomi interagenti
Raggio di Van der Waals = determina la distanza minima alla
quale possono avvicinarsi due atomi. Può essere considerato
approssimativamente come la distanza alla quale l’energia
repulsiva aumenta rapidamente (rVdW=σ).
Il raggio di Van der Waals definisce anche un'area (SVdW) e un
volume (VVdW) che rappresentano aree e volumi impenetrabili.
Il volume di Van der Waals di una molecola è dato
approssimativamente dalla somma dei volumi di Van der
Waals delle singole parti (gruppi atomici) costituenti.
S VdW
2
4
VVdW 3
3
Distanze interatomiche di contatto
Coppia di atomi
Distanza media (Å)
Distanza minima
(Å)
C--C
3.2
3.0
C--O
2.8
2.7
C--N
2.9
2.8
C--H
2.4
2.2
O--O
2.8
2.7
O--N
2.7
2.6
O--H
2.4
2.2
N--N
2.7
2.6
N--H
2.4
2.2
H--H
2.0
1.9
A grandi distanze intermolecolari possiamo prescindere da una
descrizione quantistica delle molecole e trattare le distribuzioni
di carica (nuclei ed elettroni) come delle cariche elettriche
puntiformi che seguono le leggi della fisica classica (Legge di
Coulomb).
L'energia di interazione tra una carica qi e una distribuzione di
cariche qj è data semplicemente dalla somma dei contributi
coulombiani per ogni coppia di cariche:
Vi = q i
j
qj
R ij
Fcoul
1
q1q2
2
40 R 1 2
1
q1q2
V
40 R 12
L’energia di questo tipo di interazione è dell’ordine di grandezza di
ca. 250 kJ·mol-1.
q = carica elettrica = 1.60·10-19 C = 4.8·10-10 ues
1 ues = 1 unità elettrostatica: rappresenta la carica che posta alla
distanza di 1 cm da un’altra carica unitaria la respinge con la forza
di 1 dyne (unità CGS)
0 ( H 2O ) 78
0 ( esano ) 2
Il momento di dipolo elettrico misura la distanza tra il
baricentro delle cariche positive e quello delle cariche
negative:
l
-
+
μ
Per una distanza di separazione di 1 Å:
= q · l = 4.8·10-10·1.·10-8 = 4.8·10-18 ues·cm = 4.8 D (Debye)
1 Debye = 10-18 ues·cm
Momento di dipolo per alcuni legami
legame
(D)
legame
(D)
H-F
1.9
C-F
1.4
H-Cl
1.0
C-Cl
1.5
H-N
1.3
C-N
0.2
H-O
1.5
C-O
0.1
Per la molecola di H2O:
exp=1.85 D (OH) = 1.52D = 2 (OH) cos(52.5°)
O
H
H
R12
q1
μ2
q1 2
V=
2
40 R 12
1
L’ordine di grandezza di questa interazione è di ca. 15 kJ·mol-1.
L'interazione può essere repulsiva o attrattiva a seconda della
natura della carica q1 e della orientazione reciproca tra carica e
dipolo.
L’interazione può essere attrattiva o repulsiva a seconda
dell’orientazione reciproca dei due momenti di dipolo:
+ +
+-
-+
- Per dipoli orientati in posizione fissa nello spazio (solidi):
V=-
1 2
3
R 12
int 2kJ mol -1
Per dipoli liberi di ruotare (soluzione, fase gassosa) bisogna
mediare l’interazione su tutte le possibili orientazioni:
V =-C
12 22
kT R 612
int 0.3 kJ mol -1
Una molecola neutra soggetta all’influenza di un campo elettrico
subisce un fenomeno di polarizzazione di carica.
campo elettrico
-----+++
-----+++
------
+++
molecola polarizzabile
indotto E
La polarizzabilità è una proprietà molecolare che aumenta con
il numero di elettroni che costituiscono la molecola ed è
inversamente proporzionale alla facilità di ionizzare la
molecola:
Z (numero atomico)
I(potenzia le di ionizzazio ne)
La polarizzabilità molecolare ha le dimensioni di un volume.
Il campo elettrico generato da un momento di dipolo
permanente induce un momento di dipolo (momento di dipolo
indotto) su una distribuzione di carica vicina.
Cl
H
(HCl)= 1 Debye
Benzene = 110-29 m3
V=-
12 2
R 61 2
int 0.8 kJ mol -1
Poiché il dipolo indotto assume la direzione del dipolo
inducente, l’agitazione termica (kT) non ha effetto e quindi
non compare nell’espressione dell’energia d’interazione.
Sono interazioni di natura puramente quantistica, che nascono
dalla correlazione tra i moti elettronici degli atomi interagenti.
Queste interazioni, dette anche forze di dispersione o di London,
sono presenti in tutti i sistemi, anche in molecole apolari.
Sono sempre di tipo attrattivo e possono essere descritte come
dipoli istantanei generati da fluttuazioni delle distribuzioni di
carica elettroniche.
polarizzabilità molecolare
V =-C
12 22
6
R 12
C
1 2
R 612
energia di ionizzazione
I1I 2
I1 I 2
Per due molecole di CH4 (=2.6·10-30 m3, I7 eV) a 3 Å di
distanza: εint 5 kJ·mol-1.
Interazione
ione-ione
Dipendenza Energia tipica
dalla distanza
(kJ mol-1)
R-1
250
ione-dipolo
R-2
15
dipolo-dipolo
R-3
R-6
2
0.3
dipolo-dipolo
indotto
dispersione
(London)
R-6
0.3
R-6
2
commento
solo fra ioni
dipoli fissi
dipoli rotanti
tutte le
molecole
In assenza di ioni e per sistemi liberi di ruotare in soluzione, le
interazioni dipolari sono tutte di tipo attrattivo e dipendono
tutte dall’inverso della sesta potenza della distanza.
Per questo nelle funzioni di energia potenziale vengono spesso
descritte da un termine del tipo:
V=-
C
R
6
La natura elettrostatica di queste forze è sottolineata dal fatto
che coinvolgono atomi elettronegativi in competizione per lo
stesso atomo di idrogeno.
D-(donatore) H+ - - - -A-(accettore)
Le interazioni di legame idrogeno possono essere trattate come
interazioni dipolo-dipolo:
VHB = -
C
3
R D- H - A
L’ordine di grandezza di queste interazioni è intorno ai 20
kJ·mol-1 (per R 2Å).
Lunghezza e forza del legame idrogeno dipendono dalla
elettronegatività della coppia di atomi accettore e donatore.
1.03 Å
N
O
H
1.9-2.0 Å
C












