LE TRASFORMAZIONI
GALILEIANE
TRASFORMAZIONI GALILEIANE
Per descrivere il moto di un
oggetto abbiamo bisogno di
un corpo rigido o un
ambiente ( la terra, una
stanza, una cabina etc..)
rispetto al quale misurare gli
spostamenti, di un regolo per
misurare le distanze e di un
orologio per misurare gli
intervalli di tempo. Tutti
questi oggetti costituiscono
un riferimento fisico che
indicheremo con S
Se vogliamo effettuare uno
studio analitico del moto
abbiamo bisogno anche di un
riferimento matematico, ad
esempio un riferimento
cartesiano, costituito di solito
da una terna di assi
cartesiani,
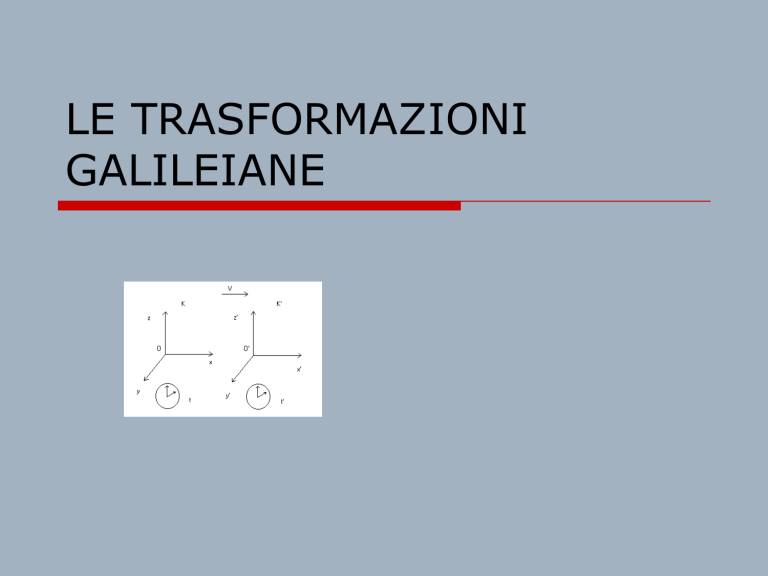
Oxyz, come in figura
Scegliendo un altro riferimento S’ (O’x’y’z’)
in generale la descrizione del moto sarà
diversa , quindi è lecito chiedersi
Come si possono calcolare gli elementi che
descrivono il moto in S’ , quando sono noti
in S
Quali sono le equazioni della
trasformazione?
Quali sono gli invarianti?
Se S’ è in quiete rispetto ad S , il problema è puramente
geometrico e si rimanda alla teoria delle trasformazioni nel
piano o nello spazio.
Se S ‘ si ottiene da S mediante una traslazione, una
rotazione, una simmetria centrale o assiale, le
trasformazioni sono di tipo isometrico e lasciano invariate
le distanze tra due punti.
Fisicamente ciò significa che le misure di lunghezze
effettuate in S’ coincidono con quelle effettuate in S
(supposto che i regoli con cui vengono effettuate le misure
siano e restino uguali )
A questa proprietà aggiungiamo che restano invariate anche
le misure degli intervalli di tempo
( supposto che gli orologi usati dagli osservatori di S e da
quelli di S’ siano stati sincronizzati all’istante t =0 e restino
sincronizzati)
Supponiamo che S’ si muova rispetto
ad S di moto rettilineo uniforme con
velocità e che all’istante t=0 , O e O’
coincidano.
La figura seguente illustra la
situazione in un generico istante t.
Chiamiamo:
OP spostamento assoluto
O’P spostamento relativo
OO’ spostamento di trascinamento
Applicando la regola della somma
vettoriale, possiamo affermare che
OP = OO’+O’P ovvero O’P=OP-OO’
Spostamento assoluto = spostamento relativo +
spostamento di trascinamento
e, passando alle rispettive componenti,:
x= x’+ ux t
x’= x - ux t
y=y’+ uy t
y’=y -uy t
z=z’+ uz
z’=z - uz t
t = t’
t ’= t
avendo aggiunto anche la relazione di uguaglianza
delle coordinate temporali
Le equazioni precedenti definiscono
le Trasformazioni classiche o
Galileiane (TG)
Relazioni analoghe possono
essere scritte anche per i
rispettivi incrementi Δx,Δy,Δz
corrispondenti ad un certo
intervallo di tempo Δt = Δt’
Δx = Δx’ + uxΔt
Δy = Δy’ + uyΔt
Δz = Δz’ + uzΔt
Δt = Δt’
Da queste si deduce una relazione anche
tra velocità assoluta ( rispetto ad S) e
velocità relativa
( rispetto ad S’)
Dividendo membro a membro per Δt=Δt’ e
ritornando alla forma vettoriale si ottiene
velocità assoluta = velocità relativa + velocità di
trascinamento
Ripetendo un procedimento analogo per le accelerazioni ,
troviamo innanzitutto
Δvx = Δv’x
Δvy = Δv’ y
Δvz = Δv’ z
In quanto le componenti della velocità di trascinamento
non variano nel tempo e quindi, dividendo membro a
membro per Δt = Δt’, e tornando alla forma vettoriale, si
deduce che
a’=a
cioè l’accelerazione è la stessa in entrambi i riferimenti
Ciò posto, è facile verificare che la distanza tra due
punti P1 e P2 è un invariante per le TG, nel senso che
, in ogni istante, risulta
P1P2 = P’1 P’2.
l’invarianza della distanza temporale va intesa
come un postulato, anche se questo fatto non à
stato messo in evidenza in tutta la Fisica
classica, fino alla critica che ne fa Einstein.
Anche la legge di composizione delle velocità ,
dimostrata matematicamente, è valida comunque
solo in conseguenza dell’invarianza del tempo.
LE TRASFORMAZIONI GALILEIANE
CONSERVANO
Parametri
Grandezze fisiche
geometrici
proiezione verticale di gli intervalli temporali
un segmento
le rette orizzontali
l’istante in cui avviene
un evento
le accelerazioni
le aree
“distanza” orizzontale le lunghezze
tra rette












