Presentazione di PowerPoint

Gli elettroni nei cristalli
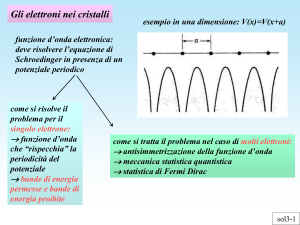
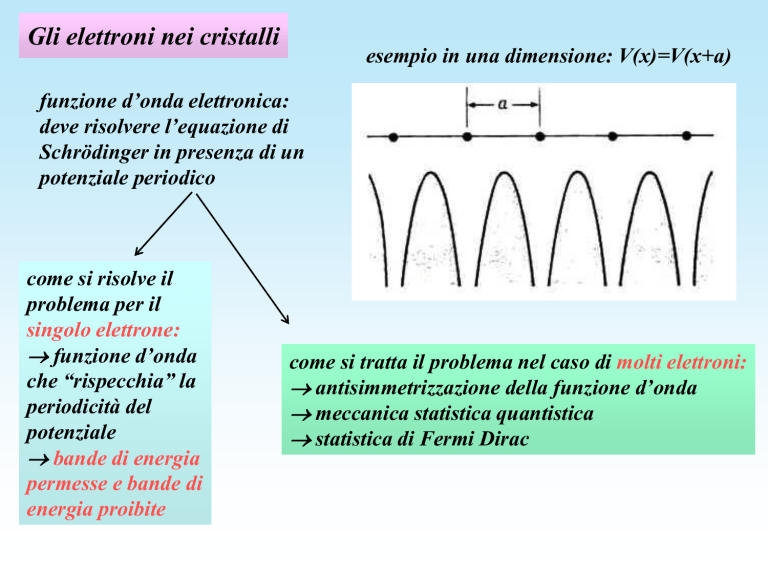
esempio in una dimensione: V(x)=V(x+a)
funzione d’onda elettronica:
deve risolvere l’equazione di
Schrödinger in presenza di un
potenziale periodico
come si risolve il
problema per il
singolo elettrone:
 funzione d’onda
che “rispecchia” la
periodicità del
potenziale
 bande di energia
permesse e bande di
energia proibite
come si tratta il problema nel caso di molti elettroni:
 antisimmetrizzazione della funzione d’onda
 meccanica statistica quantistica
 statistica di Fermi Dirac
gli elettroni nei cristalli
esempio in una dimensione: V(x)=V(x+a)
E2
E2u
E2g
E1
E1u
E1g
atomo singolo

livelli energetici
singoli
due atomi

livelli energetici
sdoppiati
E2max
E2min
E1max
E1min
molti atomi

multipletti di
livelli energetici
Due atomi: funzione
d’onda della molecola
ione-idrogeno
x
B
r
rA
A
R
1s - sigma gerade
5
1sg(r): la funzione
4
è grande
nella zona
fra4i due nuclei dove
l’elettrone
ha effetti
3
“leganti”
funzione d'onda
rB
p 2 e2 e2
R 
H el (r ) 
 
2me rA rB
z
1s(rA)
1s(rB)
3
2
2
due soluzioni, g e1 u
potenziale coulombiano
1
due livelli energetici
0
20
-7
10
-6
-5
-4
-3
-2
-1 0 1
2
z (angstrom)
3
4
5
6
7
0
1s - sigma ungerade
8
-20
1s(rA)
6
-30
4
funzione d'onda
energia (eV)
-10
-40
-50
potenziale
di attrazione
elettrone-nuclei
in
-60
funzione di z per un
-70
valore fissato di x e y
-80
-8 -7 -6 -5 -4 -3 -2 -1
0
1
z (angstrom)
2
3
4
5
6
7
8
2
0
-2
1su(r): la funzione
è nulla
-4
proprio nella-6zona fra i due
nuclei dove l’elettrone
-8
avrebbe effetti
“leganti”,
-4
-3
-2
mentre è grande nelle zone
dove ha effetti “antileganti”
1s(rB)
-1
0
1
z (angstrom)
2
3
4
funzione
d’onda
elettronica
7 “nodi”
3 “nodi”
1 “nodo”
nessun “nodo”
livelli
energetici
elettronici
gli elettroni
occupano i livelli
energetici a partire
dal più basso,
rispettando il
principio di Pauli
E1max
E1atomic
o
E1min
il solido si forma a
una distanza di
equilibrio tale da
minimizzare
l’energia
complessiva degli
elettroni che
occupano i livelli
distanza di equilibrio
molti elettroni per atomo:
 riempimento fino al livello 4
bande di
energia
 distanza di equilibrio = a
E4max
E4max
 E4atomico
E4min
E3max
E4min
E3max
E3atomic
o
E3min
E3min
E2max
E2max
E2atomic
o
E2min
E2min
E1atomic
o
bande di
energia
 E4atomico
pochi elettroni:
 si riempiono
solo i primi livelli
 distanza di
equilibrio = a’
E3atomic
o
E’2max
E’2max
E2atomic
o
E’2min
E’2min
E1atomic
E’1
o
moto di un elettrone in un
potenziale periodico:
soluzione formale
esempio in una dimensione: V(x)=V(x+a)
Hamiltoniana:
px2
H ( x) 
 V ( x)
2m
l’hamiltoniana è invariante per traslazioni di passo a (periodica): H(x)=H(x+a)
funzione d’onda: H(x) (x) = E (x)
anche  (x) deve essere invariante per traslazioni ?
Non necessariamente, ma | (x)|2 deve esserlo
| (x)|2 = | (x+a)|2
il teorema
di Bloch
per soddisfare la condizione |(x)|2 = |(x+a)|2 la
funzione d’onda deve poter essere scritta come
(x)= eikxu(x)
con u(x) invariante per traslazioni : u(x) = u(x+a)
(x) è chiamata “onda di Bloch”
verifica del teorema di Bloch:
come conseguenza dell’invarianza traslazionale, (x) può differire da (x+a)
al più per una fase:
(x+a) = ei (x)
infatti:
(x+a) = eik(x+a)u(x+a) = eika eikxu(x) = eika (x) = ei (x)
con  = ka, u(x+a) = u(x)
significato fisico dell’onda di Bloch: è il prodotto di
- un’onda piana eikx  elettrone libero
- una funzione u(x) identica sotto traslazioni di un
passo reticolare a u(x)  funzione d’onda “in
vicinanza” del singolo atomo
potenziale modulatore
periodico V(x) grande:
 si parte dalla
funzione d’onda
periodica e si include
l’effetto della fase eikx
 approssimazione di
legame forte
funzione d’onda
di Bloch
px2 ikx
2k 2 ikx
e

e
2m
2m
px  costante del moto
 k buon numero quantico
potenziale modulatore periodico V(x) piccolo:
 si parte dall’onda di elettrone libero e si corregge
per l’effetto di V(x)
 elettroni di conduzione
nei metalli;
 “quantum corral”
funzione d’onda:
approssimazione
di legame forte
 ( x )  eikx n e ik ( x  na ) ( x  na )
u ( x )  n e ik ( x  na ) ( x  na )
 ( x )  n eikna ( x  na )
u( x  a )  n eik ( x (n 1)a ) ( x  (n  1)a )
x  (x+a) equivale a cambiare n  (n-1)
potenziale periodico:
V ( x)  n E p ( x  na)
n-1
n
potenziali coulombiani
0
n+1
n-1
0,14
-1
1s
n
n+1
0,12
-2
0,10
Ep,n+
Ep,n-1
-4
-5
Ep,n
-6
1
-7
psi - atomica
energia (eV)
-3
0,08
n-1
0,06
n
n+1
0,04
-8
0,02
-9
-10
0,00
-30
-20
-10
0
10
z (angstrom)
20
30
40
-30
-20
-10
0
10
z (angstrom)
20
30
40
 (x-na) è soluzione dell’equazione di
Schrödinger per l’elettrone nell’atomo isolato
approssimazione di
legame forte
 p x2


H at ( x) ( x  na) 
 E p ( x  na)  ( x  na)  Eat  ( x  na)
 2m



Sostituendo nell’equazione di Schrödinger per l’elettrone nel reticolo:
 p x2

 p x2

ikna



H ( x ) ( x ) 
 V ( x ) n e  ( x  na ) 
  j E p ( x  ja) n eikna ( x  na )
 2m

 2m





2

ikna p x
H ( x ) ( x )  n e
 E p ( x  na )  ( x  na )  n eikna  j n E p ( x  ja)  ( x  na )
 2m



H ( x) ( x)  Eat n eikna ( x  na)  n eikna j  n E p ( x  ja)  ( x  na)
H ( x) ( x)  Eat ( x)  n eikna j  n E p ( x  ja)  ( x  na)
livello di energia atomica
modifica dovuta alle altre buche
di potenziale del reticolo
approssimazione di legame forte
Energia media:
 ( x) H  ( x)
1
 Eat  
 ( x)  ( x)
C
E
ikma *
e
 ( x  ma)
m
ikna
E
(
x

ja
)
e
 jn p
n  ( x  na) 
dove C = < (x)|(x)>
E  Eat 

1

C
1
  m  * ( x  ma)  j  m E p ( x  ja)  ( x  ma) 

C
ikma *
e
 ( x  ma)
m
ikna
E
(
x

ja
)
e
 j n p
n  m  ( x  na) 
1s
0,14
m-1
0,12
m+1
m
m+1
m
0,08
m
0,06
0,04
0,02
0,00
-30
-20
0
-10
0
10
20
potenzializ coulombiani
(angstrom)
30
psi - atomica
0,10
attrazione da
parte delle
j=m+1 buche vicine
0,08
0,06
n=m-1
0,04
0,02
0,00
40
-30
-20
0
-1
-1
-2
-2
-3
termine di
sovrapposizione
(o di risonanza)
-4
-5
-6
-7
-8
-9
-10
m
-10
0
10
20
30
40
20
30
40
potenzializ coulombiani
(angstrom)
j=m
-3
energia (eV)
psi - atomica
m-1
0,12
0,10
energia (eV)
1s
0,14
-4
-5
-6
-7
-8
-9
-10
-30
-20
-10
0
10
z (angstrom)
20
30
40
-30
-20
-10
0
10
z (angstrom)
limitandosi ai “primi
vicini” (n=m1):
E  Eat  Ecoul 

1
C

1
C

approssimazione di
legame forte
 ikma ik ( m 1) a *
e
 ( x  ma) E p ( x  ma)  ( x  (m  1)a)
m
 ikma ik ( m 1) a *
e
 ( x  ma) E p ( x  ma)  ( x  (m  1)a )
m
E  Eat  Ecoul 

1 ika  ika
e
e
C
m  *( x  ma) E p ( x  ma)  ( x  (m  1)a) 
E  Eat  Ecoul  Eov cos(ka)
dove:
Ecoul 
E ov 
1
C
1
  m  * ( x  ma)  j  m E p ( x  ja)  ( x  ma) 

C

m

 * ( x  ma) E p ( x  ma)  ( x  (m  1)a)


termini di overlap
Ep(x-ma) <0 (potenziale
attrattivo)
k=8 kmin

overlap positivo:
 (x-ma) e  (x-(m-1)a)
hanno lo stesso segno

k=4 kmin
contributo negativo
all’energia di overlap

k=2 kmin
overlap negativo
 (x-ma) e  (x-(m-1)a)
hanno segno opposto

contributo negativo
all’energia di overlap
k=kmin
a partire da ciascun livello atomico
E
prima “zona di Brouillin”
Ea
approssimazione di
legame forte
Eoverlap
t
Ecoul
-/a
-G/2
0
/a
G/2
E  Eat  Ecoul  Eov cos(ka)
k
bande
E4atomico
E4min
E3max
E3atomico
E3min
E2max
E2atomico
E2min
E1atomico
E1max E1min
bande di energia permesse e bande proibite
bande di energia permesse e bande proibite
Passaggio da una banda all’altra
eccitazione radiativa da
una banda alla banda
superiore
(se permessa dal principio
di Pauli)
E = E3min- E2max
E3min
E2max
E2min
E = E2min- E1max
E1max
sol3-18
Hamiltoniana di una
particella libera:
p x2
H ( x) 
2m
Il problema del
trasporto
funzione d’onda: H(x) (x) = E (x)
elettrone libero
2m
eikx  
25
2 2
 k ikx
e
2m
px  costante del moto
 k buon numero quantico
(k ) 2
E
2m
20
energia (eV)
px2
15
10
relazione di
dispersione
parabolica
5
k (angstrom^-1)
0
-3
-2
-1
0
1
2
3
v
velocità di gruppo:
 1  1 E k p
v


 
k  k  k m m
k
velocità di fase e
velocità di gruppo
onde singole
due onde
k1= 1 Å-1
k2= 1,05 Å-1
1,5
1,0
0,5
ampiezza
4 onde
k1= 1 Å-1 ; k2= 1,05 Å-1
k3= 1,1 Å-1 ; k4= 1,15 Å-1
0,0
-0,5
-1,0
sovrapposizione
5,0
-1,5
4,0
0
20
40
3,0
60
80
x(angstrom)
ampiezza
2,0
sovrapposizione
1,0
5,0
0,0
4,0
-1,0
3,0
-2,0
2,0
x
-4,0
-5,0
0
20
40
60
80
100
120
x(angstrom)
xk 2
Δx  Δk  Δx  Δp  2  h
140
ampiezza
-3,0
1,0
0,0
-1,0
160
-2,0
-3,0
-4,0
-5,0
0
100
200
300
x(angstrom)
400
500
moto dell’elettrone libero in presenza di una forza esterna
dv 
F
F

dt ; dk  dt  dv  dk
m

m
1 dE
dv
1 d 2E

; dv 
v
dk 
dk

dk
2
 dk
dk
 dk
m
elettrone libero
25
20
15
10
5
k (angstrom^-1)
0
-3
1
1 d E
 2
m  dk 2
-2
-1
0
v
2
schermo


F  eEel
energia (eV)
in presenza di una forza esterna,
dovuta ad es. a un campo elettrico, il
“pacchetto” che all’istante t aveva un
certo numero d’onda ko e velocità vo,
all’istante (t+dt) ha numero d’onda
(ko+dk) e velocità (vo+dv) con:
Vel
catodo
1
2
3
dk
k
per l’elettrone libero,
d2E/dk2=costante,
quindi m=costante
moto di un elettrone nel cristallo in
presenza di una forza esterna
E
V


F  eEel
in presenza di una forza esterna, dovuta
ad es. a un campo elettrico, il “pacchetto”
di onde di Bloch che all’istante t aveva un
certo numero d’onda ko e velocità vo,
all’istante (t+dt) ha numero d’onda
(ko+dk) e velocità (vo+dv) con:
1 E
v
 k
1
1 d 2E
 2
m  dk 2
per l’elettrone nel cristallo, d2E/dk2
non è costante, quindi m non è
costante  “massa efficace”
zone di massa efficace negativa
l’elettrone si comporta come se avesse
carica elettrica positiva  “buca”
Riflessione al bordo di zona
riflessione al
bordo di zona
La massa efficace a piccoli k
Evoluzione temporale
della funzione d’onda:
elettrone libero
25
1
1 d 2E
 2
m  dk 2
per l’elettrone
libero,
d2E/dk2=costante,
quindi m=costante
20
energia (eV)
 (x,t) = ei(kx-ωt)
dove E  
15
10
5
k (angstrom^-1)
0
-3
-2
-1
0
1
2
3
E
per l’elettrone nel cristallo:
d2E/dk2 = - Eoverlap a2 cos(ka)
a piccoli k:
d2E/dk2 = - Eoverlap a2 (1-(ka)2/2)
k
-/a
0
/a
bande con gap diretta e con gap indiretta nel Si
gap diretta
gap indiretta
a = 0,543 nm
bande con gap diretta e con gap indiretta nel Ge
gap indiretta
gap diretta
a = 0,565 nm
Risonanza ciclotronica e misura della massa efficace
Moto (classico) di un elettrone in un campo magnetico:
B
Se l’elettrone entra nella zona del campo
magnetico B con una velocità v perpendicolare
a B descrive un’orbita circolare con raggio r e
pulsazione ω = v/r dati da:
* 2
forza
“centrifuga”
mv
 evB
r
forza di
r
v
tipico esperimento
Lorentz
eB
 *
m
due modi di condurre la misura:
-B fisso e scan in ω della microonda
- ω fisso e scan in B
B
direzione
della corrente
campione
microonda
Effetto Hall e misura del segno della carica elettrica
La forza di Lorentz devia le cariche elettriche che viaggiano con
componente vx della velocità sono deviate nella direzione dell’asse y
creando un campo elettrico Ey che compensa la forza di Lorentz:
eE y  evB 
jx B
eVH
B

I
a
n
ahn
-jx è la densità di
corrente jx= nev
tipico esperimento
z
-n è la densità
elettronica
B
y
B
 VH 
I
ehn
RH 
B
ehn
x
I
h
VH
a
campione
RH è la “resistenza di Hall; permette di
- conoscere il segno della carica
elettrica
- determinare la densità elettronica n