Misure elettriche ed
elettroniche
1° anno Corso di Laurea TSRM
Dr. Francesco Lisciandro
1
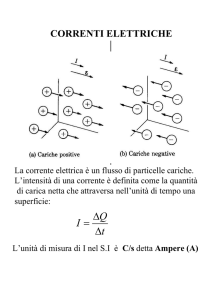
Corrente elettrica
E’ un movimento ordinato di cariche elettriche
che di solito avviene all’interno di un
conduttore, ma non necessariamente: ad
esempio a volte le cariche sono messe in
movimento nel vuoto (vd. tubi a raggi X)
2
Corrente continua e corrente
variabile
corrente continua
c o rre n te
Se le cariche fluiscono
con successione e moto
uniforme, si ha la
corrente continua, cioè
una corrente costante nel
tempo
Se la velocità delle
cariche non è costante, si
ha una corrente
variabile nel tempo
60
40
20
0
0
1
2
3
4
5
4
5
tempo
corrente variabile
c o rre n te
60
40
20
0
0
1
2
3
tempo
3
Intensità di corrente
-
-
-
-
-
A
-
Corrente continua:
Q
I
t
Corrente variabile:
dq
i
dt
Si misura in Ampere (A) :
E’ la quantità di
carica Q che passa
attraverso la
sezione A
nell’unità di tempo
(1 s)
1 coulomb
1 ampere
1 secondo
Oss.: 1 coulomb = 1 ampere x 1 secondo = 1 A s
4
La corrente è generata da un moto di cariche
che possono essere sia positive che negative.
In natura è più frequente il movimento di
elettroni liberi (negativi) ma nonostante ciò si
considera positivo il verso della corrente
dovuta a movimento di cariche positive,
cioè quello contrario al moto degli elettroni;
si parla di verso convenzionale della corrente.
5
La corrente si misura con
strumenti detti
amperometri, che
vengono inseriti nel
A
conduttore in modo da
i
essere attraversati da
tutte le cariche in
movimento
La densità di corrente è il rapporto fra
l’intensità di corrente I e la superficie S della
sezione retta A attraverso la quale la corrente
fluisce. J I per una distribuzi one di corrente uniforme
S
dI
J
se la distribuzi one non è uniforme
dS
6
Esercizio 1
Su
un conduttore giungono e successivamente
sono trascinate via 1012 elettroni al secondo e
1012 cariche positive tetravalenti ogni 10 s.
Si determini il valore della corrente I in mA
7
Soluzione 1
Qtot(-) = -1,602 x 10-19 x 1012 = -1,602 x 10-7 C
I(-) = Qtot(-)/t = -0,16 x 10-6 A = -0,16 mA
Qtot(+) = 4 x 1,602 x 10-19 x 1012 = 6,4 x 10-7 C
I(+) = Qtot(+)/t = 6,4 x 10-7 A = 0,064
I = I(+) + I(-) = -0,16 mA + 0,064 mA = -0,096
mA
8
Esercizio 2
Un cavo è costituito da 3 tubicini conduttori
isolati fra loro
1
-
++
2
2A
+++++
3
A
1A
5A
B
Trovare il valore ed il verso della corrente nel
tratto AB
9
Soluzione 2
Percorrendo il conduttore da A verso B si ha:
I = -I1 + I2 – I3 = -1 +2 – 5 = -4 A
Si ha quindi come risultante una corrente di 4
Ampere diretta da B verso A
10
Esercizio 3
Un elettrone ruota nel vuoto ad una velocità
costante v = 200000 km/s su un’orbita circolare
di raggio r = 10 m
Trovare la corrente i che attraversa una generica
sezione A della traiettoria
11
Soluzione 3
i = Q/1 s (attraverso A)
In un secondo e- percorre d = 200 x 106 m e
A passa attraverso A n volte dove:
n = d/(2 p r) = 200 x 106 /6,28 x 10 = 3,183 x 106
(sono i giri in un secondo fatti da e-)
ev
Q = e x n = - 1,602 x 10-19 x 3,183 x 106 = - 5,1 x 10-13 C
Quindi:
i = 0,51 x 10-12 A ed è diretta nel verso contrario al moto
dell’elettrone
12
Esercizio 4
Sapendo che in 1 mm3 di Cu ci sono 8,4*1019
atomi, trovare la velocità con cui si spostano gli
elettroni di conduzione (ce n’è uno per ogni
atomo) nel Cu stesso per dare luogo ad una
corrente di densità J = 4 A/mm2
13
Soluzione 4
Consideriamo un cubetto di Cu di lato 1 mm
a
u
Gli elettroni impiegano t ad attraversare a, dando luogo
ad una corrente di 4 A. Si ha dunque:
I = Q/t = 8,4*1019*1,602*10-19/t = 4
Sia u la velocità; si ha: t = d/u = 10-3 m/u e quindi:
4 = 8,4*1,60*u/10-3 e quindi:
u = 4*10-3/(8,4*1,6) = 0,298*10-3 m/s
14
Tensione elettrica
Per ottenere un moto ordinato di cariche occorre agire
su di esse dall’esterno in modo opportuno. I dispositivi
che permettono di realizzare un flusso di cariche
ordinato nel senso desiderato sono detti generatori
elettrici.
Essi servono a fornire alle cariche l’energia sufficiente a
mantenersi in movimento. In pratica convertono in
energia elettrica altre forme di energia (energia
meccanica nel caso delle dinamo, energia chimica nel
caso delle pile, energia luminosa nel caso delle
fotocellule, etc.)
15
Differenza di potenziale (d.d.p.)
Caratterizza i generatori.
+
G
e-
W Q V
V
W
Q
Le cariche negative fluiscono
spontaneamente nel conduttore e
tornano al polo positivo. Al suo interno,
invece, il generatore deve compiere un
lavoro per spostare gli elettroni dal + al –
Ciò implica i due morsetti si trovano a
diverse energie potenziali.
W è la differenza di en. potenziale
(lavoro), Q è la carica da spostare, V
è la d.d.p. del generatore
Convenzionalmente si usa
questa scrittura; V è detta
anche TENSIONE
16
Tensione
Se tra due punti si manifesta una differenza di potenziale V, si
può quindi dire in modo del tutto equivalente che tra di essi
esiste una tensione V.
La d.d.p. di un generatore (a morsetti aperti) viene detta forza
elettro-motrice (f.e.m.)
La tensione rappresenta una grandezza fisica con una propria
unità di misura.
V si misura in Volt
1 volt = 1 joule/1 coulomb
Per la misura pratica delle tensioni si usano
strumenti detti voltmetri, i quali hanno due
morsetti che devono essere inseriti in
corrispondenza dei punti fra i quali interessa
eseguire la misura
G
V
17
Esercizio 5
Si calcoli il valore della d.d.p. ai morsetti aperti di
un generatore sapendo che l’energia posseduta da
ciascun elettrone libero sul polo negativo è pari a
2*10-15 J.
18
Soluzione 5
La d.d.p. è espressa da V =
W/Q
Nel nostro caso Q è la
carica dell’eQ = 1,602*10-19 C
mentre W = 2 *10-15 J
Pertanto:
15
W
2 10
V
124,8 V
19
Q 1,602 10
19
Problema 6
Che
cosa indica il termine elettronvolt (eV)?
Soluzione 6
Esso indica un’energia; ad esempio è l’energia
potenziale posseduta da una carica elettrica pari a
quella dell’elettrone, quando esse è sottoposta alla
d.d.p. di un volt.
20
Problema 7
Quanti
elettronvolt corrispondono ad 1 joule?
Soluzione 7
Poiché: 1 eV = 1,602*10-19 C * 1 J
segue che:
1 joule = 1 / 1,602*10-19 = 6,24*1018 eV
21
Resistenza elettrica
Il movimento delle cariche avviene con
maggiore o minore difficoltà a seconda della
natura fisica del materiale.
Ciò è dovuto che nel loro moto ordinato, le
cariche sono soggette a qualcosa di simile ad un
“attrito” da parte del materiale (che infatti si
scalda al passaggio della corrente).
La corrente elettrica non può mantenersi nei
corpi spontaneamente, a causa di questo
“attrito”: occorre fornire continuamente energia
per consentire alla corrente di fluire
22
Materiali conduttori, semiconduttori
ed isolanti
I corpi non si comportano tutti allo stesso modo
quando sono attraversati da corrente.
I materiali si dicono conduttori se i loro atomi
possiedono elettroni periferici liberi (e- di conduzione)
e/o se danno luogo a ioni liberi. La conduzione ha
grado più o meno elevato a seconda dell’attrito fornito
alle cariche libere
Gli isolanti, invece, sono materiali che non hanno
elettroni liberi; tutti gli elettroni sono vincolati al nucleo
Nei semiconduttori, il grado di conduzione è
intermedio fra conduttori ed isolanti, ed il passaggio di
carico avviene solo se si verificano alcune condizioni
particolari.
23
Legge di Ohm
Al variare della tensione applicata ad un conduttore, la
corrente che lo attraversa varia nella sua intensità… ma
come?
Esiste una proporzionalità diretta tra il valore della
tensione V e quello della corrente I:
V=R*I
Il Coefficiente di proporzionalità R dipende dalle
caratteristiche del corpo percorso da corrente e prende
il nome di Resistenza, perché rappresenta il grado di
difficoltà che le cariche libere trovano nel muoversi
entro i corpi
24
Resistenza elettrica
R è una grandezza fisica, con una unità di
misura (ohm, simbolo Ω)dedotta dalla legge di
Ohm:
1 volt
1 ohm
Da R = V / I segue che
1 ampere
L’inverso della Resistenza è detto Conduttanza,
che può essere espressa da:
1
I
G
R V
25
Resistività (r)
E’ detta anche resistenza specifica e permette di
calcolare la resistenza di un corpo a partire dalle sue
caratteristiche fisiche e geometriche. Per un corpo
filiforme ed omogeneo, di sezione A e lunghezza l, si
ha:
l
R r
A
Si verifica facilmente che r si misura in ohm * metro
26
Problema 8
Calcolare il diametro e la lunghezza di un
conduttore di Cu (r = 1,7 mΩ*cm, densità di
corrente massima ammessa 5 A/mm2) per il
quale la caduta di tensione deve essere di 0,5 V
quando è percorso da una corrente di 10 A
27
Soluzione 8
La resistenza del conduttore è:
R = V/I = 0,5/10 = 0,05 Ω
Se la densità è 5 A/mm2, e la corrente è 10 A,
allora la sezione S è pari a 2 mm2 ed il diametro
sarà
d 2
La lunghezza è invece:
S
p
1,6 mm
0,05 2 106
l
5,71 m
8
r
1,75 10
R A
28
Legge di Ohm per un circuito chiuso
La somma algebrica delle f.e.m. che agiscono nel circuito è pari
alla somma algebrica delle cadute di tensione sui vari elementi
resistivi presenti.
I due generatori agiscono in maniera
discorde, quindi le f.e.m hanno
segno opposto, ad esempio + per E1
e – per E2.
Su ogni R abbiamo una caduta di
tensione data dalla legge di Ohm. Si
ha pertanto:
E1 E2 I Ri1 I Ri 2 I Ru
E1 E2
da cui : I
Ri1 Ri 2 Ru
29
Legge di Ohm per un circuito chiuso
Se indichiamo con E le
f.e.m. concordi al verso
della corrente I e con Ec
quelle discordi (forze
contro-elettro motrici –
f.c.e.m.) la legge pe ri
circuiti chiusi può essere
scritta come:
SE-SEC = ISR
30
Esempio numerico
Sia: E1 = 100 V; E2 = 30 V,
E3 = 10 V, SR = 10 Ω
La corrente I sarà:
E1 E2 E3 100 30 10
I
6A
SR
10
Dato che il valore di I trovato
è positivo, si conferma che il
verso rappresentato in figura
è corrispondente al verso
della corrente
31
Problema 9
Determinare per il circuito in (a) la corrente I (intensità
e verso) e la d.d.p. fra H e K
32
Soluzione 9
Poiché E2-E1 = I*SR, si ricava I = 2A. Il verso è quello concorde
alla I di figura (b)
VHK è la somma delle cadute di tensione nel percorso HDCH.
Poiché VCH = 0, si ha VHK = VHD + VCK (sono positive).
Applicando la legge di Ohm si ha:
VHK = Ri1*I+Ri2*I = 0,2*2 +0,3*2 = 1 V
33
Legge di Ohm generalizzata
La legge di Ohm si presta ad essere utilizzata per
determinare la d.d.p. ai capi di un bipolo o tra due punti
di un tronco di circuito percorso da corrente:
La d.d.p. VMN tra due punti generici M e N di un
tronco è data dalla somma algebrica delle f.e.m. e dalla
somma delle cadute di tensione (R*I) che devono essere
considerate positive se la corrente va da M a N e
negative in caso contrario
VMN Ei I R j
i
j
34
Esempio
Applichiamo la regola ai due tronchi MABN e MCDN
MABN VMN = Ri1*I1 – E1 +R1*I1
MCDN VMN = Ri2*I2 + E2 + R2*I2
35
Problema 10
Determinare il verso ed il valore di I
sapendo che VAB = 200 V
36
Soluzione 10
Supponendo I diretta da A verso B si ha:
VAB = E1-E2+(Ri1+Ri2+R)*I e quindi
200 = 240-20 + (3+16+1) da cui:
I = (200-240+20)/(3+1+16)= -1 A
Il segno negativo indica che il verso di I indicato in
figura è sbagliato e che la corrente fluisce da B
verso A
37
Problema 11
Sapendo che I va fisicamente da A verso B e ha
un’intensità di 2 A, calcolare la d.d.p. agli estremi
del tronco
38
Soluzione 11
Abbiamo due differenti possibilità per risolvere il
problema: calcolando la somma delle singole cadute di
potenziale lungo il tratto, oppure applicando
direttamente la legge di Ohm generalizzata
1° modo: VAB = VAP + VPQ + VQB cioè
VAB = 60 – 2*6 – 80 = - 32 V
2° modo: VAB = E1 – E2 –R*I cioè
VAB = 60 – 80 – 2*6 = - 32 V
In entrambi i casi risulta che A è a potenziale negativo
rispetto a B!
39
Prima legge di Kirchoff
La somma delle correnti entranti in un nodo è sempre uguali
alla somma delel correnti uscenti dallo stesso nodo
I nodi sono i punti nei quali confluiscono le correnti.
La prima legge di Kirchoff esprime l’equilibrio esistente fra le
correnti in un nodo e ubbidisce al principio più generale della
conservazione della carica elettrica
I
entranti
I
i
I uscenti
0
i
40
Esempio pratico
Applicando il primo principio al nodo A si ha:
I5 + I8 = I1 o anche -I1 +I5 + I8 = 0
41
Estensione della prima legge di
Kirchoff
Presa una superficie chiusa
che taglia alcuni lati di una
rete, la somma algebrica delle
correnti dei lati tagliati dalla
superficie deve essere nulla.
Ad esempio, dalla figura, si può
dedurre che
indipendentemente dai valori
delle correnti, vale sempre:
I4 = I3 + I7
42
Seconda legge di Kirchoff
Per ogni maglia, la somma algebrica delle f.e.m.
presenti è pari alla somma algebrica di tutte le
cadute di tensione sulle resistenze presenti sui rami
della maglia stessa.
La maglia è un qualsiasi percorso chiuso
all’interno di una rete elettrica.
E R
j
j
z
Iz
z
43
Esempio pratico
Considerando la maglia ABFA:
-E1 + E5 = (Ri1 + R1)*I1 – R6*I6 + (Ri5 + R5)*I5
44
Problema 12
Determinare i valori delle correnti sui tre
lati della maglia e quello della corrente
uscente da A
45
Soluzione 12
Nodo A: ICA-IAB-IA = 0
Nodo B: IB+IAB-IBC = 0
Nodo C: IC+IBC-ICA = 0
Maglia ABCA:
EA-EB+EC=RAIBC+RBICA+RCIAB
Il sistema di equazioni delle correnti permette
di esprimere tutte le correnti dell’equazione di
maglia in termini della sola IBC
46
Soluzione 12 – parte seconda
L’equazione di maglia diventa così:
EA-EB+EC = (RA+RB+RC)*IBC+RBIC-RCIB
-28 = 16*IBC + 36
IBC = -4 A da cui:
ICA = 0; IAB = - 6 A
da IA = ICA-IAB segue IA = 6 A
47
Soluzione 12 – parte 3
La soluzione era immediata
considerando l’estensione
del primo principio di
Kirchoff!!
IA = IB + IC = 2 + 4 = 6 A
48