file

Le funzioni:
definizioni e classificazioni
Funzioni e grafici
Le funzioni: definizioni e classificazione
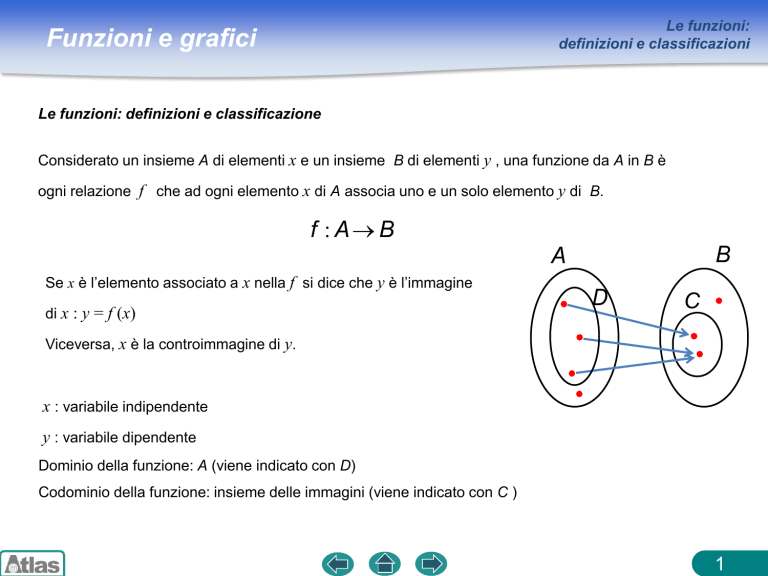
Considerato un insieme A di elementi x e un insieme B di elementi y , una funzione da A in B è
ogni relazione f che ad ogni elemento x di A associa uno e un solo elemento y di B.
f : A® B
B
A
Se x è l’elemento associato a x nella f si dice che y è l’immagine
di x : y = f (x)
D
C
Viceversa, x è la controimmagine di y.
x : variabile indipendente
y : variabile dipendente
Dominio della funzione: A (viene indicato con D)
Codominio della funzione: insieme delle immagini (viene indicato con C )
1
Funzioni e grafici
Le funzioni:
definizioni e classificazioni
Funzioni suriettive, iniettive, biiettive
Una funzione si dice:
a. suriettiva se il codominio coincide con B, cioè non ci sono
elementi y in B che non hanno controimmagini in A.
La funzione in fig.a è suriettiva se consideriamo come
insieme B quello degli y che sono maggiori o uguali a -2:
ogni retta parallela all’asse x la incontra in almeno un
punto.
b. iniettiva se a elementi distinti di A corrispondono elementi
distinti di B.
La funzione in fig.b è iniettiva: ogni retta parallela all’asse x
la incontra al massimo in un punto;
c. biiettiva se è sia suriettiva che iniettiva.
La funzione in fig.c è biiettiva; ogni retta parallela all’asse x
la incontra in uno e un solo punto.
Delle funzioni biiettive si dice che sono delle corrispondenze biunivoche tra
gli elementi dell’insieme
elemento di
A e quelli dell’insieme B , vale a dire che ad ogni
A viene associato un solo elemento di B e viceversa.
2
Le funzioni:
definizioni e classificazioni
Funzioni e grafici
La funzione inversa
f : A ® B è invertibile se la relazione che si ottiene scambiando gli insiemi A e B,
cioè x Î B e y Î A , è ancora una funzione; la funzione inversa si indica con il simbolo f -1 ed è:
Una funzione
f -1 : B ® A
Le funzioni suriettive e quelle iniettive non sono di norma invertibili, quelle biiettive lo sono sempre.
Per trovare l’equazione dell’inversa di una funzione invertibile basta scambiare le variabili
risolvere l’equazione ottenuta rispetto a
rispetto alla bisettrice
x ey
e
y. Il grafico della funzione inversa si ottiene per simmetria
y  x.
3
Le funzioni:
definizioni e classificazioni
Funzioni e grafici
ESEMPIO
Troviamo l’inversa della funzione
•
y  3x  6
La funzione è invertibile perché è biettiva; infatti, a valori
diversi di x corrispondono valori diversi di y.
f a 3a  6
ed è
•
f b  3b  63a  6  3b  6
3a  6  3b  6
se e solo se
•
a b
Troviamo l’equazione dell’inversa scambiando i ruoli di
x  3y  6 
Il grafico della funzione
6
xe y
6
1
y  x2
3
y  3x  6
è quello in colore blu;
quello dell’inversa (in rosso) è il suo simmetrico rispetto alla
bisettrice del primo e del terzo quadrante.
4
Le funzioni:
definizioni e classificazioni
Funzioni e grafici
La funzione composta
f : A B
g : B  C, si dice funzione composta di f
h : A  C che si ottiene applicando la g agli elementi ottenuti dalla f .
Per indicare che h è il prodotto di f e g scriviamo:
Date due funzioni
e
e
g la funzione
h  g  f x
ed è
ESEMPIO
Date le funzioni:
f x   x  2
g x   x3 , calcoliamo:
e
a.
b.
f
g
x  x  2  x  2
quindi
g
f
x  x  x3  2
3
h  g f  x  2
3
quindi
3
k  f g  x3  2
5
Le funzioni:
definizioni e classificazioni
Funzioni e grafici
Le funzioni reali di variabile reale
La classificazione
Possiamo classificare le funzioni in base alla forma dell’espressione analitica che le definisce in:
•
Funzioni algebriche: funzioni la cui espressione algebrica contiene solo operazione di addizione,
sottrazione, moltiplicazione e divisione, elevamenti a potenza ed estrazioni di
radice nella variabile
•
x.
In tutti gli altri casi si dice che la funzione è trascendente.
6
Le funzioni:
definizioni e classificazioni
Funzioni e grafici
Funzioni
Trascendenti
Algebriche
1
y = x + 2 tan x; y = ex + 3x; y = ln ;.....
x
Razionali
Irrazionali
y= x +2
Intere
y = x2 - 7x5
Fratte
y=
5- x
x2 - 3
7
Le funzioni:
definizioni e classificazioni
Funzioni e grafici
Le funzioni definite per casi
Una funzione si dice definita per casi se è definita da espressioni
diverse a seconda del valore assunto da
x.
ESEMPIO
2 x  3 se x  1
y 2
se x  1
 x
8
Funzioni e grafici
Le funzioni:
definizioni e classificazioni
Tra le funzioni definite per casi possiamo annoverare anche quelle che contengono moduli.
ESEMPIO
y = x +1
 x  1 se x  1
y
 x  1 se x  1
1
-1
9
Le funzioni:
definizioni e classificazioni
Funzioni e grafici
Funzioni crescenti e decrescenti
Consideriamo una funzione
due punti di
f ( x) definita in un insieme D e nell’intervallo I Í D ; siano x1e x2
I . Diciamo che:
a.
f ( x) è crescente in I
b.
f ( x) è decrescente in I se quando x1 < x2 allora f ( x1 ) > f ( x2 )
se quando
x1 < x2 anche f ( x1 ) < f ( x2 )
10
Le funzioni:
definizioni e classificazioni
Funzioni e grafici
Funzioni pari e dispari
Sia
f ( x) una funzione di dominio D ; diciamo che:
•
f ( x) è pari se
f (-x) = f ( x)
per ogni
xÎ D
•
f ( x) è dispari se
f (-x) = - f ( x)
per ogni
xÎ D
ESEMPIO
•
La funzione
f ( x) = x4 + 2 è una funzione pari:
f (-x) = (-x) + 2 = x4 + 2 = f ( x)
4
Grafico simmetrico rispetto all’asse y
11
Le funzioni:
definizioni e classificazioni
Funzioni e grafici
•
La funzione
f x   x3
è una funzione dispari:
f  x    x    x3   f x 
3
Grafico simmetrico rispetto all’origine
•
La funzione
f x   x3  2
è una funzione né pari, né dispari:
f  x    x   2   x3  2
3
Grafico non simmetrico rispetto
all’asse y e all’origine
12
Le funzioni:
definizioni e classificazioni
Funzioni e grafici
Funzioni periodiche
Una funzione
f ( x) si dice periodica di periodo T,
con
T > 0, se si verifica che:
f ( x+T ) = f ( x)
Con
T numero intero qualsiasi.
13
Funzioni e grafici
y  sin x e la funzione y  cos x sono periodiche di periodo 2.
•
La funzione
•
La funzione y
•
La funzione
 tan x è periodica di periodo  .
y  sin kx e la funzione y  cos kx sono periodiche di periodo 2 .
k
Esempio: La funzione
•
Le funzioni:
definizioni e classificazioni
y  sin 3 x, essendo k  3 , è periodica di periodo T 
y  tan kx è periodica di periodo  .
k
3
3
La funzione y  tan x , essendo k 
2
2
2 2
 
3
3
La funzione
Esempio:
, è periodica di periodo

2
T  
3 3
2
14
Funzioni e grafici
Il dominio naturale di una funzione
Il dominio naturale di una funzione
Il dominio naturale di una funzione
y = f ( x) , detto anche insieme di definizione o campo di
esistenza, è sempre un sottoinsieme, proprio o improprio, dell’insieme dei numeri reali che dipende
dalle operazioni che compaiono nell’espressione di
f ( x)..
Per esempio:
•
La funzione
y = x4 - 6 ha dominio R: D = (-¥,+¥)
•
La funzione
y=
1
x2 - 4
x2 - 4 ¹ 0
ha dominio l’insieme
x ¹ ±2
Þ
R esclusi i punti che annullano il denominatore:
D : (-¥,-2) È (-2, 2) È ( 2,+¥)
15
Funzioni e grafici
Il dominio naturale di una funzione
ESEMPIO
Determiniamo il dominio della funzione
La funzione esiste per i valori di
x-1³ 0
2- x¹ 0
x>0
y=
x -1
+ ln x
2- x
x che soddisfano il seguente sistema:
per l’esistenza del radicale (indice pari)
per l’esistenza della frazione
per l’esistenza del logaritmo
Risolvendo otteniamo:
x ³1
x¹2
x>0
La cui soluzione è
Quindi:
x ³1 Ù x ¹ 2
D = (1, 2) È ( 2,+¥)
16
Funzioni e grafici
Il segno di una funzione
Il segno di una funzione
Una volta determinato il dominio, si possono ricavare altre informazioni sul grafico della funzione
f ( x).
 Intersezioni con gli assi cartesiani
•
I punti di intersezione con l’asse
y = f ( x)
y= 0
•
x si determinano risolvendo il sistema:
Le soluzioni dell’equazione
f ( x) = 0 , se esistono,
vengono detti zeri della funzione.
Una funzione può avere al massimo un punto di intersezione con l’asse
y che, se esiste, si
determina risolvendo il sistema:
y = f ( x)
x=0
Cioè valutando
f ( 0)
 Studio del segno
Studiare il segno di una funzione significa individuare gli intervalli del dominio in cui la funzione
assume valori positivi e quelli in cui assume valori negativi.
Cioè equivale a risolvere la disequazione
f ( x) > 0 .
17