La Funzione Esponenziale

La Funzione Esponenziale un
modello matematico della realtà

La matematica, scoperta o invenzione che sia, è nata
per risolvere problemi concreti e, anche se nel corso
dei secoli è diventata sempre più astratta e generale,
costituisce uno strumento formidabile d’indagine
della realtà in quanto offre numerosi modelli per
interpretare i fenomeni naturali.

Un modello interessante di numerosi fenomeni è
rappresentato dalla Funzione Esponenziale.
Prof. Biasco 2006-07
1
La Funzione Esponenziale
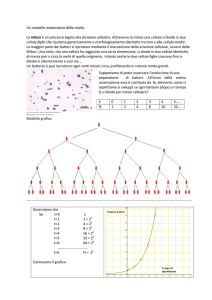
1 - La riproduzione dei batteri

La maggior parte dei batteri si riproduce mediante il meccanismo
della scissione cellulare (mitosi).

Una volta raggiunta una dimensione opportuna, ogni batterio si
divide in due cellule identiche, di massa pari a circa la metà di
quella originaria. A loro volta, le due cellule figlie si accrescono fino
a dividersi ulteriormente. Un batterio si può riprodurre ogni venti
minuti circa, proliferando in colonie abbastanza grandi da essere
visibili a occhio nudo

Vogliamo studiare l’evoluzione di una popolazione iniziale di No
batteri dopo k cicli riproduttivi.
Prof. Biasco 2006-07
2
Gli archeobatteri
costituiscono un gruppo
di batteri adattati a vivere
in condizioni ambientali
estreme.
Methanospirillum
hungatii è un
archeobatterio
metanogeno Gramnegativo, presente in
ambienti privi di ossigeno
di paludi e stagni; esso
trasforma l'anidride
carbonica in metano.
Nella foto, il
microrganismo è
osservato mediante
microscopio elettronico a
trasmissione, e appare in
fase di scissione, ovvero
mentre si sta dividendo
per dare luogo a due
cellule figlie.
Archeobatterio in fase di divisione
Prof. Biasco 2006-07
3
Colonia di streptococchi
Prof. Biasco 2006-07
4
Nel gruppo degli streptococchi, batteri Gram-positivi, sono comprese numerose
specie patogene per l'uomo, quali S. pneumoniae (pneumococco), responsabile
della polmonite e di alcune forme di meningite, e S. pyogenes, agente di alcuni
tipi di tonsillite, dell'endocardite, della febbre reumatica, della piodermite e della
scarlattina. A seconda della specie, l'azione patogena scaturisce da componenti
della capsula che riveste la cellula, oppure da composti che vengono riversati
all'esterno (esotossine). Alcuni streptococchi trovano impiego nell'industria delle
preparazioni alimentari, come nel caso della produzione dello yogurt e del kefir,
in cui si sfrutta il metabolismo fermentativo di S. bulgaricus e S. termophilus.
Nell'immagine, ottenuta al microscopio elettronico a scansione, è visibile una
colonia di S. pyogenes le cui cellule, di forma tondeggiante (cocchi) appaiono
disposte in fila, caratteristica tipica della gran parte degli streptococchi.
Prof. Biasco 2006-07
5
La Funzione Esponenziale
k
0
N
1
1
2
2
4
3
8
4 16
5
32
Prof. Biasco 2006-07
6
La Funzione Esponenziale
quindi
num batteri
Stadio zero
1
Stadio 1
2 = 21
Stadio 2
4 = 22
Stadio 3
8 = 23
Stadio 4
16 = 24
Stadio 5
32 = 25
Stadio 6
64 = 26
Stadio k
N = 2k
Prof. Biasco 2006-07
7
La Funzione Esponenziale
32
16
8
4
1
0
1
2
3
4
5
Stadio riproduttivo
Prof. Biasco 2006-07
8
La Funzione Esponenziale
In generale

Se allo stadio iniziale i batteri sono No.
Stadio zero
No = No20
Stadio 1
N1 = 2No = No21
Stadio 2
N2 = 2N1 = No22
Stadio 3
N3 = 2N2 = No23
Stadio 4
N4 = 2N3 = No
24
Stadio 5
N5 = 2N4 = No25
Stadio 6
N6 = 2N5 = No26
Stadio k
Nk = 2Nk-1 = No2k
Prof. Biasco 2006-07
Nella formula compare il
termine esponenziale
2k
9
La Funzione Esponenziale
No = 5
Prof. Biasco 2006-07
10
La Funzione Esponenziale

In generale
DEF se a  R+
a1
la funzione:
f: x  R -----------> y = ax  R+
si dice Funzione Esponenziale di base a.
Prof. Biasco 2006-07
11
La Funzione Esponenziale
Problemi sui batteri
1.
Supponendo che la riproduzione di un batterio avvenga ogni 20
minuti calcolare quante ore occorrono affinché una popolazione
iniziale di 10 batteri raggiunga il numero di 109 unità.
2.
Calcolare il numero di cellule che si originano da 20 cellule dopo
15 cicli riproduttivi.
3.
Dopo 9 cicli riproduttivi si ha una popolazione di 220160 batteri.
Calcolare il numero iniziale di batteri.
Prof. Biasco 2006-07
12
La Funzione Esponenziale
2 - Un deposito bancario
o
o
Quando versiamo dei soldi in banca riceviamo un
compenso che è l’interesse.
L’interesse è il prezzo che la banca paga per poter
disporre del nostro denaro.
Il tasso d’interesse i (opp r) normalmente è espresso
in percentuale
es. i = 5%
su 100 euro depositati la banca dà 5 euro d’interesse.
Prof. Biasco 2006-07
13
La Funzione Esponenziale
Il calcolo dell’interesse può essere fatto principalmente
in due modi:
Interesse Semplice o Interesse Composto
o
o
Nell’interesse semplice il calcolo dell’interesse viene
fatto una sola volta alla fine del periodo
d’investimento
Nell’interesse composto l’interesse è calcolato alla
fine di ogni anno e si capitalizza, cioè diventa nuovo
capitale su cui si calcola un nuovo interesse.
Prof. Biasco 2006-07
14
La Funzione Esponenziale
Interesse Semplice
Un capitale iniziale di 10.000 euro viene investito ad un
tasso annuo del 4% per 5 anni. Calcolare l’interesse
semplice e il montante finale.
C = 10.000
o
i = 4%
t = 5 anni
Il calcolo dell’interesse semplice è dato dalla
formula:
I = C i t
Oss. L’interesse è direttamente proporzionale al capitale, al
tasso d’interesse e al tempo.
Prof. Biasco 2006-07
15
La Funzione Esponenziale
Interesse Semplice
Quindi
4
I  10000
5  100  4  5  2000
100
Alla fine dei cinque anni d’investimento avremo un
Montante
Montante = Capitale + Interesse
M = C + I = 10.000 + 2000 = 12.000 euro
Prof. Biasco 2006-07
16
La Funzione Esponenziale
Nella tabella seguente è riportato l’interesse e il montante relativi
ad un investimento di 10.000 euro al tasso del 20% a interesse
semplice Investimento di anni Interesse
Montante
0
1
2
3
4
5
6
7
8
9
10
0
2.000
4.000
6.000
8.000
10.000
12.000
14.000
16.000
18.000
20.000
Prof. Biasco 2006-07
10.000
12.000
14.000
16.000
18.000
20.000
22.000
24.000
26.000
28.000
30.000
17
La Funzione Esponenziale
Interesse Semplice
35000
30000
25000
20000
Interesse
Montante
15000
10000
5000
0
0
2
4
6
8
Montante e Interesse sono linearmente
dipendenti dal tempo
Prof. Biasco 2006-07
10
12
Anni investimento
18
C = 1 euro
interess
e
La Funzione Esponenziale
20%
6%
4%
anni
L’interesse semplice è direttamente proporzionale al tempo e aumenta
all’aumentare del tasso d’interesse
Prof. Biasco 2006-07
19
La Funzione Esponenziale
Interesse Composto annuo
Lo stesso capitale iniziale di 10.000 euro viene ora
investito ad un tasso annuo del 4% per 5 anni ad
interesse composto annuo.
Calcolare l’interesse e il montante finale.
C = 10.000
i = 4%
t = 5 anni
Per risolvere il problema calcoliamo interesse e
montante anno per anno:
Prof. Biasco 2006-07
20
La Funzione Esponenziale
Inizio investimento = stadio zero
C = 10000
Fine primo anno = stadio 1
I1 =10000*4%*1 = 400
M1 = 10000+400 = 10400
Fine 2° anno = stadio 2
I2 =10400*4%*1 = 416
M2 = 10400+416 = 10816
Fine 3° anno = stadio 3
I3 =10816*4%*1 = 432,64
M3 = 10816 + 432,64 = 11248,64
Fine 4° anno = stadio 4
I4 =11248,64 *4%*1 = 449,95
M4 = 11248,64+ 449,95 =11698,59
Fine 5° anno = stadio 5
I5 = 11698,59* 4%*1 = 467,94
M5 = 11698,59 + 467,94 = 12166,53
Prof. Biasco 2006-07
21
La Funzione Esponenziale
Nella tabella seguente è riportato l’interesse e il montante per lo
stesso investimento di 10.000 euro al tasso del 20% a interesse
composto
anni
0
1
2
3
4
5
6
7
8
9
10
Interesse
2.000
2.400
2.880
3.456
4.147
4.977
5.972
7.166
8.600
10.320
Montante
10.000
12.000
14.400
17.280
20.736
24.883
29.860
35.832
42.998
51.598
61.917
Prof. Biasco 2006-07
22
La Funzione Esponenziale
Interesse composto
250000
200000
150000
100000
50000
0
0
2
4
6
Il Montante è funzione esponenziale del tempo
8
10
anni
Prof. Biasco 2006-07
12
14
16
18
Anni investimento
23
La Funzione Esponenziale
Formula generale dell’interesse composto
inizio
Mo = C
anno 1°
M1 = C + I = C + C r  1= C (1+r)
anno 2°
M2 = M1+ I = M1+ M1r 1= M1(1+r)= C(1+r)(1+r) = C(1+r)2
anno 3°
M3 = M2+ I = M2+ M2r 1= M2(1+r)= C(1+r)2(1+r) = C(1+r)3
anno k°
Mk = C(1+r)k
Nella formula compare il termine esponenziale
Prof. Biasco 2006-07
(1+r)k
24
La Funzione Esponenziale
Problemi sull’interesse
1.
Calcolare il montante ottenuto investendo 50.000 euro al tasso del 3% per 10
anni nel caso di interesse semplice e di interesse composto annuo.
2.
Un investimento di 8 anni al tasso del 2% ha prodotto il montante di 29.291,48
euro, Calcolare il capitale iniziale.
3.
4.
5.
Quanti anni deve durare l’investimento di 12.000 euro al tasso del 2% per
produrre un montante di 17.831 euro?
Il sig. Antonio marito della sig.ra Cesira si vanta di aver ottenuto 70.548 euro
investendo in buoni postali 30.500 euro per 6 anni. Spiega perché il signor
Antonio racconta frottole.
La Banca Popolare di Soldopoli ci propone due tipi d’investimento il primo ad
interesse semplice del 6% e il secondo ad interesse composto annuo del 4% .
Stabilire in quale caso risulta conveniente il primo e in quale caso il secondo.
Prof. Biasco 2006-07
25
La Funzione Esponenziale
Ottave di DO
3 - Le note musicali

Le vibrazioni degli oggetti producono suoni o rumori: ess. Vibrazione
delle corde di una chitarra o di un pianoforte, della membrana di un
tamburo, delle corde vocali, vibrazione del piano del tavolo ……

Il nostro orecchio è in grado di percepire soltanto i suoni che hanno una
frequenza compresa tra 16 e 16.000 Hz circa.

Quando la vibrazione avviene tutta alla stessa frequenza viene prodotto un
suono puro.
Una corda di pianoforte che vibra a 263 Hz produce un DO centrale, a
526 Hz il DO della 1° ottava superiore a 1052 il DO della 2° ottava
superiore……...

Se la frequenza è di 440 Hz si ha un LA centrale, se 880 Hz si ottiene un LA
più acuto, cioè il LA della 1° ottava superiore. ……
Prof. Biasco 2006-07
26
La Funzione Esponenziale
Scala di LA
Tabella delle frequenze del LA
Distanza in ottave
dal LA centrale
LA centrale
ottava
-4
-3
-2
-1
0
1
2
3
4
5
frequenza
Hz
27,5
55
110
220
440
880
1760
3520
7040
14080
Prof. Biasco 2006-07
27
La Funzione Esponenziale
Frequenze del LA
16000
14000
12000
10000
8000
6000
4000
2000
0
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
7
8
9
La frequenza di vibrazione è funzione
esponenziale dell’ottava
Prof. Biasco 2006-07
10
11
12
Distanza in ottave
28
La Funzione Esponenziale
Allora se indichiamo con
Distanza in ottave
dal LA centrale
LA centrale
fo = 440 Hz = freq. LA centrale avremo:
ottava
frequenza frequenza Hz
-4
-4
27,5
2 f0
-3
55
2-3 f0
-2
110
2-2 f0
-1
220
2 f0
0
440
f0
1
880
2f0
2
1760
2 f0
3
3520
2 f0
4
7040
2 f0
5
14080
25 f0
Prof. Biasco 2006-07
-1
2
3
4
29
La Funzione Esponenziale
se k è la distanza in ottave dalla nota centrale la frequenza è data da:
fk = f02k
Nella formula compare il termine esponenziale
2k
Oss. Il discorso precedente è valido per tutte le altre note musicali.
Prof. Biasco 2006-07
30
La Funzione Esponenziale
Altri fenomeni che hanno andamento
esponenziale


Decadimento radioattivo
Carica e scarica del condensatore

Attenuazione della radiazione elettromagnetica

Tensione di vapore saturo

Modello Malthusiano della crescita della popolazione
Prof. Biasco 2006-07
31
La Funzione Esponenziale
Bibliografia



Brandi, Salvadori - Modelli matematici elementari - Bruno
Mondadori
Scovenna - Profili di matematica 1 - Cedam
AA.VV. - Materiali scaricarti da internet
Prof. Biasco 2006-07
32