Capitolo_4_conduttori

Campo elettrostatico nei conduttori
Conduttori: cariche mobili sotto l’azione di E
STATICA: cariche fisse  Eint. = 0
Eint =0 (Vint = cost)  ·Eint= 0  int = 0
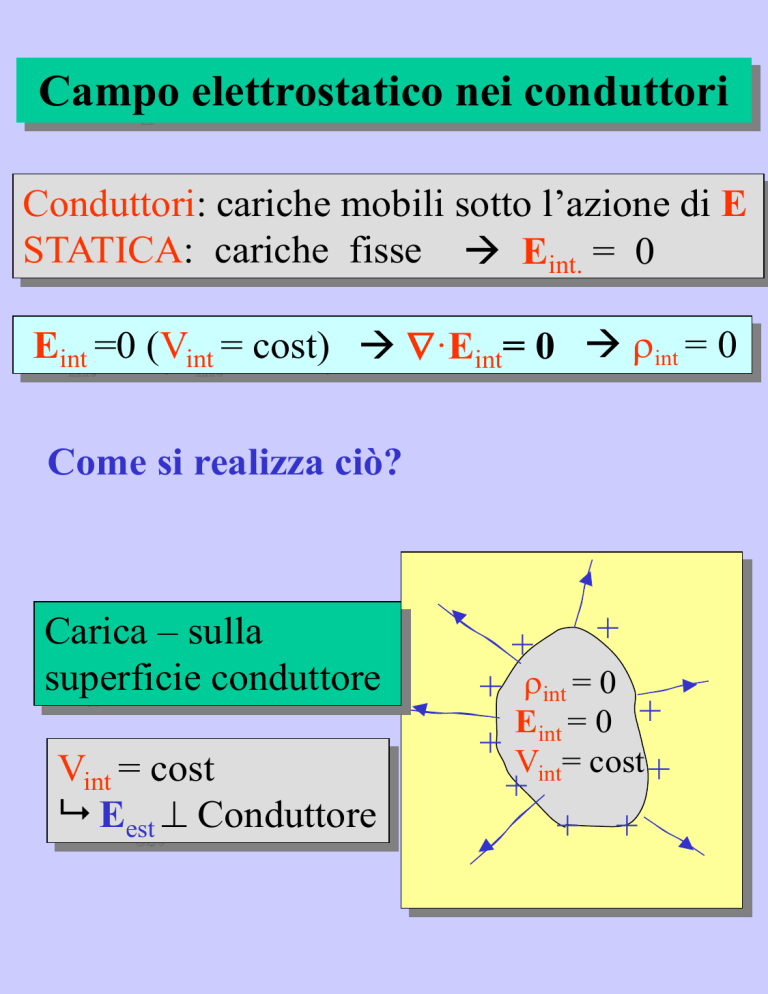
Come si realizza ciò?
Carica – sulla
superficie conduttore
Vint = cost
 Eest  Conduttore
+
+
+ int = 0
Eint = 0 +
+ V = cost
+
+ int
+ +
Conduttore in Eesterno
+
+
+
-
+
-
-
Eint = 0
int = 0 +
Vint= cost
+
+
-
-
-
carica indotta sulla superficie del
conduttore  Eint = 0
Campo elettrostatico in prossimità
della superficie dei conduttori
dq

+
dS+
+ Eint = 0
+
+
+
+
+
+
S (chiusa)
area base A
A
 S (E)  AE 
o

E  nˆ in prossimità della
0
superficie del cond.
Campo elettrostatico nelle cavità di
conduttori
 S (Ec )  0
nella cavità
 qi  0
S
+
+
+
Ec = 0
+
+
?- +
E
i
+
-B
+?
+
B
A+
+
+
+
E  dl  VAB  0
+
A
+
+
+
Ma il conduttore è
equipotenziale

Ecavita’ = 0  gabbia di Faraday
Gabbia di Faraday- funziona al contrario?
S
In generale
NO
|qi| = q
Collegando
conduttore
a Terra
SI
+
+
+
Ec =0
qi
- + +q +
+
- - +
+
+
-
Ec =0
- + - - -
+
+
+
+
Esempio:
campi di un conduttore a forma sferica
q
E(r) 
rˆ
2
4o r
rR
+
+
+

q
V( r )   E(r)  dr 
4o r
r
+
+
+r
+
+
R
+
+
Come nel caso di una
carica puntiforme
rR
Ec  0
(gabbia di Faraday)
q
V  cost 
4o R
Capacità di un conduttore
C  q / V (Faraday F)
Carica q  potenziale V (rispetto )
(dipende dalla geometria del conduttore)
dipende dalla geometria del conduttore
Esempio: SFERA
+ +r
+

+
q
V   E(r)  dr 
4o R
R
+
+
+
+
R
+
+
q
4o R
C
 q
 4o R
q
V
Capacità di un conduttore sferico
Capacità di un condensatore ( Es: sferico)
r
Condensatore:
- + + ++
- + R1 + +
+
+
- +R - 2-
2 conduttori caricati
con +q e -q
C = q/(V1-V2)
r  R 1 , r  R2 E  0
R1  r  R2
E(r) 
q
4o r 2


R1
R2
R2
^r
V1  V2   E(r)  dr   E(r)  dr
q
1
1
V1  V2   E(r)  dr 
( 
)
4o R1 R2
R1
R1 R2
C  4o (
)
R2  R1
Capacità di un condensatore cilindrico
L
R1
r
rR1; r R
R2
2
E0
q ^
E(r) 
r
2o rL
R1  r  R 2
Gauss
R2
q
R2
V1  V2   E  d r 
ln
2o L R 1
R1
C  2o L / ln( R2 / R1 )
Capacità di un condensatore piano
Area A
+ +
D
+
- -
+
+
E
+ + +
- - ^n
Approssimazione doppio strato:
Eest =0 Eint= /o ;  =dq/dS

V1  V2   E dr 
D
o
P
P2
1
εo A
σA
C

σ/ε o D
D
Rappresentazione grafica di condensatore
Q
A
VAB= Q / C
B
C
Condensatori in parallelo
Q1
C1
A
B
Qtot= Q1 + Q2
C2
Q2
VAB= Q1 /C1 = Q2 /C2
Situazione “equivalente“
Qtot
A
Ceq
B
Ceq= ?
VAB Ceq = Qtot= Q1 + Q2 = VAB C1+ VAB C2
 Ceq= C1+ C2
Cparal = C1+C2+…Cn
Predomina la + grande
Condensatori in serie
Q
Q
C2
A C1
B
Q1 = Q2=Q
C
VAB= VAC +VCB= Q /C1+ Q /C2
Situazione “equivalente“
Q
A
Ceq
B
Q = VAB Ceq
Q/ Ceq = VAB = Q /C1+ Q /C2
 1/ Ceq=1/ C1+1/ C2
1/Cserie =1/ C1+1/ C2+….1/ Cn
Predomina la + piccola
Energia immagazzinata in
condensatore carico
Condensatore con carica q: V= q / C  U(q)
×
Lest.carica= U(q) – U(0)
Per calcolo di U(q)  situazione intermedia:
condensatore carico con q’<q  V’= q’ / C
Per aggiungere ulteriore carica dq’
 dLest.carica= dq’(V’- V ) = dq’(q’ /C)
×
q
2
1q 1 2
q'dq'

 CV  U(q)
Lest.carica  
2C 2
C
0
Densità d’energia del campo elettrico
Condensatore piano: area A separazione
delle facce D
εo A
C
;
D
σ
q
E

;
εo
Aεo
2
1
1
1q
2
2

ε
E
V wV

ε
E
AD
U
o
o
2
2C 2
1
dU densità di energia
2
w  εo E 
2
dV
1
dU
2
Risultato generale
w  εo E 
2
dV
Densità di carica sui conduttori: effetto punte
E1
+
+
+
q1 +
V1 = V2
+
R1 +
+
+
++
+
+
+
+ R2+
+ +q
2
q1
q2   qi
i

4 Ri2
4o R1 4o R2
2
E2
E2
i=1,2
R1
i
i=1,2
 1
Ei 
R2
o
R1
 E1
E2  E1
R2