Potenziale elettrostatico
Moto di una carica
r
r inr campo elettrico
r
fi
qE = m a
F = qE
Lavoro della forza elettrostatica:
La forza di Coulomb è una forza posizionale.
è una forza conservativa.
B
Energia potenziale:
r r
DU = U ( B) -U ( A ) = - LAB = - q Ú E ⋅ d s
A
DEFINIZIONE :
La differenza di potenziale elettrostatico tra due punti A e B è
definita come il lavoro cambiato di segno per portare la carica
unitaria da A a B.
B
r r
LAB
= - Ú E ⋅ds
DV = V ( B) - V ( A) = q
A
UNITÀ DI MISURA:
volt = 1 joule / 1 coulomb
r
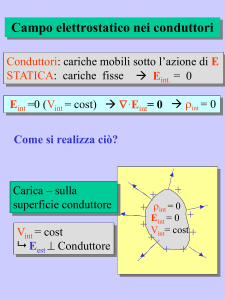
In condizioni statiche all’interno di un conduttore E=0
fi Nel conduttore il potenziale è uniforme
fi Il conduttore è equipotenziale
Di norma si assume lo zero del potenziale all'infinito, cioè a
grande distanza dalla cariche generanti il campo.
A
r
r
V ( A) = - Ú E ⋅ d s
•
Poiché la Terra può essere considerata come un corpo conduttore,
l'espressione mettere a terra, che esprime il fatto di collegare un
corpo alla Terra con un conduttore, significa che il conduttore è a
potenziale zero.
POTENZIALE ELETTROSTATICO GENERATO DA UNA CARICA
PUNTIFORME q
r
E =
1 q ^
r
2
4pe0 r
fi
r
r
r
V ( A) = - Ú E ⋅ d s = - Ú
A
rA
1
1 q dr = - q
Ú
2
2 dr =
pe
pe
4 0 •r
•4 0 r
A
•
q
=4pe0
È 1 ˘r r
q
=
ÍÎ- r ˙˚
4pe 0 rA
r =•
=
A
POTENZIALE ELETTROSTATICO GENERATO DA UN INSIEME
DI CARICHE PUNTIFORMI qi
A
r
r
r
r
(
)
V A = - Ú E ⋅ d s = - Ú Â iEi ⋅ d s = A
•
•
r
r
= - Âi Ú E i ⋅ d s =
r
r
Ei ⋅ d s =
A
Ú Âi(
•
A
 iVi
•
=
1
4pe o
)
Âi q i
ri
ri è la distanza tra il punto A e il punto dove si trova la carica qi
POTENZIALE ELETTROSTATICO DI UN CONDUTTORE
In condizioni statiche un conduttore è equipotenziale.
fi Il valore del suo potenziale elettrostatico è quindi ben definito
Potenziale elettrostatico di una sfera conduttrice di raggio a e carica Q:
V =
1 Q
4pe 0 a
Condensatore
È un oggetto che immagazzina energia elettrica, sotto forma di
energia potenziale di un campo elettrico.
Due conduttori carichi con cariche opposte +q , -q.
–q
+q
E’ generato un campo fi c’è una differenza di potenziale V (µq)
Per scaricare il condensatore il campo fa un lavoro
fi ENERGIA POTENZIALE
CAPACITÀ DI UN CONDENSATORE
C=
q
V
UNITÀ DI MISURA DI CAPACITÀ:
farad =
1 coulomb
1 volt
CAPACITÀ DI UN CONDUTTORE ISOLATO (rispetto alla terra)
Capacità di una sfera conduttrice di raggio a:
C=
q
/
= 4pe0a
1 q
/
4pe 0 a
Condensatore piano
E=
+q
q
s
=
e 0 e0 A
r r
r r
=
F⋅ds
=
qE
· ds
dL
–q
Area
A
Il campo è
uniforme
d
d
r r
qd
=
=
=
⋅
Ú
V
E ds Ed
e0 A
0
C=
q
q
=
qd
V
e0A
fi
C=
e0 A
d
ENERGIA IMMAGAZZINATA IN UN CONDENSATORE
Lavoro per spostare da un conduttore all'altro un po' di
carica dq', quando la carica sul condensatore è q' e la
sua differenza di potenziale è V' :
d L = V ¢ dq ¢ =
q¢
d q¢
C
Lavoro richiesto per caricare il condensatore da zero al
valore finale di carica q :
q
q¢
1 q2
L = Ûd L =Û d q ¢ =
C
2C
0
1
2
L = CV
2
1
L = qV
2
L’energia immagazzinata nel campo è quindi:
1
U = CV 2
2
DENSITÀ D’ENERGIA (energia per unità di volume):
U
1 CV 2 1 e0 A V 2 e0 V
u=
=
=
=
Vol 2 Ad 2 d Ad 2 d
fi
e0 E 2
u=
2
2