Le reti neurali
Simona Balbi
Cosa sono le reti neurali
Una rete neurale artificiale (A)NN è un paradigma di
elaborazione dell’informazione ispirato al modo in cui i
sistemi nervosi biologici, come il cervello umano,
elaborano l’informazione
L’elemento chiave di questo paradigma è la struttura
dell’informazione, concepita come un grande numero di
elementi (i neuroni) interconnessi, che lavorano
contemporaneamente, al fine di risolvere problemi
specifici
Le NN, come le persone, imparano dall’esempio e
dall’esperienza. Ogni NN è configurata per una specifica
applicazione, ad esempio di classificazione, attraverso un
processo di apprendimento. Nei sistemi biologici
l’apprendimento implica adattamenti delle connessioni
sinaptiche presenti fra i neuroni. Eì questo che cerca di
mimare una ANN
Un po’ di storia
Le (A)NN sembrano qualcosa di abbastanza recente, ma in
realtà hanno avuto una vita piena di alti e bassi, entusiasmi e
frustrazioni. Nascono prima dell’avvento dei computer,
anche se i maggiori sviluppi si sono avuti con il diffondersi di
calcolatori potenti ed economici
La loro storia è comunque segnata dalla multidisciplinarietà,
che vede prevalentemente l’impegno congiunto di
neuroscienziati e informatici, ma poi matematici e statistici
Il primo neurone artificiale fu prodotto nel 1943 dal
neurofisiologo Warren McCulloch e dal logico Walter Pits
La tecnologia disponibile all’epoca non li portò molto lontano
Quando ricorrere alle reti neurali?
NN sono in grado di estrarre informazioni da dati complicati e imprecisi
Sono quindi estremamente utili nel riconoscere regolarità e nell’individuare
tendenze troppo complesse per essere colte da un essere umano che
utilizzi strumenti di analisi classici
Una NN addestrata può essere immaginata come un “esperto” e può servire per
predire nuove situazioni e simularne altre, in condizioni del tipo "what if"
I principali vantaggi di NN sono:
1.
Capacità di apprendimento: attraverso opportuni algoritmi dinamici la rete
riesce ad adattare il proprio comportamento fino a computare una
funzione arbitraria y= f (x) in base agli esempi presentati.
2.
Capacità di generalizzare: il sistema che abbia correttamente appreso una
funzione riesce di norma a fornire una risposta "ragionevole" anche a
stimoli precedentemente mai occorsi
3.
Tolleranza agli errori: scostamenti non significativi dei valori di input
vengono assorbiti dalla rete, diminuendo così il rumore statistico
4.
Tolleranza ai guasti La presenza di molte unità di elaborazione in parallelo
fa sì che l'eventuale perdita di una unità abbia conseguenze non
irreparabili
Le novità computazionali delle NN
Le NN differiscono nell’approccio dai consueti programmi
informatici, poiché il loro “ connessionismo ” si contrappone alla
concezione “ logico-simbolica ” tipica della Intelligenza Artificiale
e della programmazione classica
I programmi consueti di regola si basano su un approccio
algoritmico: una sequenza di istruzioni nota e specificata viene
eseguita al fine di risolvere in problema. Questo vuole dire che
risolvono problemi di cui è nota la soluzione
NN elaborano l’informazione come un cervello umano: i neuroni
lavorano in parallelo per un comune obiettivo
NN non sono programmate per eseguire un compito specifico,
poiché apprendono da esempi, che devono essere scelti con cura
Lo svantaggio è che trovano la soluzione da sole e sono quindi
imprevedibili. D’altra parte l’approccio cognitivo tradizionale della
programmazione è totalmente prevedibile e se qualcosa non
funziona è un problema di hardware o di software
Cosa è NN
Da un punto di vista “ matematico ” :
data una funzione G : X → Y, nota attraverso
un insieme di coppie
{ (xp,G(xp)) : xp X, p = 1, . . . , P }
una rete neurale è un particolare modello di
approssimazione di G :
F (· , w) : X → Y
dipendente da un vettore di parametri w
(tipicamente nonlineare rispetto ai parametri)
1
Cosa è NN
2
Da un punto di vista “ statistico ”, una rete
neurale `e un particolare modello di regressione
(di solito, non lineare) o di classificazione
Se concepiamo un percettrone stocastico nella
forma più semplice, come
y=g(x,θ)+ noise
dove x è l’input, y l’output e g(x,θ) una funzione
di attivazione non lineare, parametrizzata da θ,
allora cogliamo immediatamente la somiglianza con
un modello statistico non lineare
Il PERCETTRONE
Una rete costituita da un singolo strato di
neuroni formali è chiamata Perceptron
(Rosenblatt, 1962) ed è stato proposto un
algoritmo per il calcolo dei pesi, noto come
“Perceptron learning rule” che fornisce in
un numero finito di iterazioni i parametri w, θ
se i campioni sono linearmente separabili,
aggiustando i pesi in corrispondenza di ciascun
esempio
Il neurone artificiale
(da Grippo, Sciandronehttp://www.dii.unisi.it/~agnetis/grippo1.pdf)
E’ un dispositivo per il quale
y = h (Si wi xi – q)
assume valore 1 se la somma algebrica pesata degli
ingressi supera un valore di soglia θ e –1 altrimenti, dove:
• y {−1, 1} uscita
• xi R ingressi (anche xi {0, 1})
• wi R pesi
• θ R soglia
• h : R → R funzione di attivazione h(t) = 1 t ≥ 0;
h(t) = −1 t < 0
Il neurone formale pu`o realizzare le operazioni logiche NOT,
AND, OR
NN come classificatore lineare
Poniamo y(x) = sign(wT x − θ)
Fissati w, θ, il neurone può essere interpretato
come un classificatore lineare , che assegna il
vettore x alla classe A oppure alla classe B in
base al valore di y(x), ossia, ad es.:
x A se y(x) = 1, x B se y(x) = −1.
I parametri w, θ possono essere determinati a
partire da un insieme di campioni xp di cui è
nota la classificazione dp {−1, 1}, risolvendo
(se possibile) rispetto a (w, θ) il sistema
(xp)Tw − θ ≥ 0, se xp A,
(xp)Tw −θ < 0, se xp B
p = 1, . . . , P
Un’impostazione alternativa è quella di sostituire la funzione di
attivazione sign con una funzione continuamente differenziabile
g di tipo sigmoidale, ossia una funzione monotona crescente
tale che:
lim g(t) = −1
lim g(t) = 1
t→−∞
t→∞
come, ad esempio tanh(t) = et − e−t
et +e−t
e minimizzare l’errore quadratico
Analisi del sistema di apprendimento
di una rete neurale
Questo è un grafo di dipendenza per una NN:
la variabile h è un vettore a 3-dimensioni e dipende da x, variabile di input.
La variabile g è un vettore a 2-dimensioni e dipende da h.
Infine, f, la variabile di output output dipende da g.
In questa rete, i vettori variabile possono essere ulteriormente decomposti
in unità parallele: h1, for example, is independent of h2 dato x.
Christos Dimitrakakis 2005
Reti feedforward
Una rete neurale feedforward :
è rappresentata da un grafo orientato
aciclico (a differenza delle cosìddette reti
ricorrenti, al cui interno sono previsti cicli
è costituita da un certo numero di strati
(una, percettrone, più rete multistrato),
ciascuno formato da un certo numero di
neuroni
La rete multistrato
1
Ogni strato riceve segnali da quello precedente, li elabora e passa
il risultato allo strato successivo
Gli strati intermedi hanno tutti le stesse caratteristiche
strutturali, mentre il primo e l'ultimo sono particolari:
il primo riceve segnali dall'esterno e li passa semplicemente allo
strato successivo e quindi alla rete
l'ultimo riceve i segnali, pesati secondo i valori delle connessioni,
dallo strato precedente, li somma e passa all'esterno il risultato (la
funzione di attivazione dell'ultimo strato è semplicemente
l'identità, così che in uscita si ha un qualunque numero reale (come
è naturale che sia se si intende usare la rete per approssimare
funzioni a valori reali)
un neurone che si trova nello strato i-esimo riceverà uno o più
ingressi che possiamo indicare con:
ui = [ u1i, u2i, … umi ]
dal precedente (i – 1)-esimo strato e produrrà in uscita un segnale
ui+1 = [ u1i+1, u2i+1, … um+1i+1 ]
La rete multistrato
2
I valori
ui+1 = [ u1i+1, u2i+1, … um+1i+1 ]
dove il generico uji+1 = s(hi+1),
dove hki+1 = Sj uji wijk + bki
dove Wi = ( wijk) è la matrice dei pesi sulle connessioni
e bi = (bik) è il vettore di bias, coefficienti applicati ad
un'unita'fittizia che genera un segnale sempre pari a 1, e
pertanto non e' necessario rappresentarla nel disegno
I segnali, sia in ingresso che in uscita possono assumere un
qualsiasi valore continuo compreso tra 0 e 1 e
La struttura di una NN
Una rete neurale, costituita da n strati, ciascuno dei quali
composto da mi neuroni, sarà caratterizzata da n-1
matrici di dimensione mi-1×mi (per i=1, …, n) e da n-1
vettori riga bi di dimensione mi
Possiamo allora costruire le (mi-1+1×mi)-matrici Wi ed i
vettori mi+1 dimensionali
Si è così definita una funzione di tante variabili reali quanti
sono i neuroni dello strato di input, a valori in uno spazio
euclideo di dimensione uguale al numero di neuroni
presenti nello strato di output.
Questa funzione dipende da un gran numero di parametri e
ciò la rende estremamente versatile nel modellare i più
vari comportamenti
Il rischio è che lo siano troppo
L’apprendimento
APPRENDIMENTO significa applicare una classe di funzioni data
F ad un insieme di osservazioni al fine di trovare una funzione f*
F che risolve il problema in modo ottimale
Si definisce una funzione di costo C : F → tale che la soluzione
ottimale C(f*) C(f) f F
C fornisce la misura di quanto è lontana da noi la soluzione ottimale
del problema che vogliamo risolvere
Esistono diversi schemi di algoritmi di apprendimento che cercano
nello spazio delle soluzioni al fine di trovare una funzione che abbia
il minor costo possibile
La funzione di costo può essere definita ad hoc o si possono
utilizzare funzioni di costo che godano di alcune proprietà
desiderate (es. convessità) o sceglier una particolare formulazione
del problema (ad esempio probabilistica, la probabilità a posteriori
come inverso del costo)
La funzione di costo dipende dal l’obiettivo
Paradigmi di apprendimento
apprendimento supervisionato (supervised learning)
OBIETTIVO: previsione del valore dell'uscita per ogni valore
valido dell'ingresso
INPUT : untraining set, ossia un insieme di dati per i quali si
conosce il risultato (coppie di valori input – output)
PROCEDURA: la rete impara ad inferire la relazione che lega i dati
al risultato
COME: la rete è addestrata mediante un opportuno algoritmo
(tipicamente, la backpropagation), il quale usa tali dati allo
scopo di modificare i pesi ed altri parametri della rete stessa in
modo tale da minimizzare l'errore di previsione (costo) relativo
all'insieme d'addestramento
La rete deve essere dotata di un'adeguata capacità di
generalizzazione, con riferimento a casi ad essa ignoti. Ciò
consente di risolvere problemi di regressione o classificazione
apprendimento non supervisionato
(unsupervised learning)
OBIETTIVO: raggruppare i dati d'ingresso e individuare
pertanto cluster rappresentativi dei dati stessi
INPUT : insieme di dati di cui è noto solo l’ingresso
PROCEDURA: algoritmi d'addestramento che modificano i
pesi della rete facendo esclusivamente riferimento ad un
insieme di dati che include le sole variabili d'ingresso.
COME mediante algoritmi che ricorrono a metodi topologici
o probabilistici
L'apprendimento non supervisionato è anche impiegato per
sviluppare tecniche di compressione dei dati.
apprendimento rinforzato
(reinforcement learning)
Ricalca le procedure di condizionamento classico (premi/punizioni)
OBIETTIVO: individuare un modus operandi, a partire da un processo
d'osservazione dell'ambiente esterno
INPUT : alla rete viene fornita solo una informazione qualitativa sulla
bontà della sua risposta (del tipo “giusto” o “sbagliato”)
PROCEDURA: gli algoritmi per il reinforcement learning tentano in
definitiva di determinare una politica tesa a massimizzare gli incentivi
cumulati: i pesi sono modificati in modo da aumentare la probabilità di
ottenere premi e diminuire la probabilità di ricever punizioni
COME: un agente, dotato di capacità di percezione, che esplora un
ambiente nel quale intraprende una serie di azioni; ogni azione ha un
impatto sull'ambiente, e l'ambiente produce una retroazione (in termine di
incentivi o disincentivi) che guida l'algoritmo stesso nel processo
d'apprendimento
L'apprendimento con rinforzo differisce da quello supervisionato poiché
non sono mai presentate delle coppie input-output di esempi noti, né si
procede alla correzione esplicita di azioni subottimali. Inoltre, l'algoritmo è
focalizzato sulla prestazione in linea, la quale implica un bilanciamento tra
esplorazione di situazioni ignote e sfruttamento della conoscenza corrente
Algoritmo di Backpropagation
L'algoritmo di backpropagation è utilizzato nell'apprendimento supervisionato
e permette di modificare i pesi delle connessioni in modo tale che si minimizzi
una certa funzione errore E (regola delta generalizzata): per ogni esempio
fornito in ingresso si valuta l'errore in uscita rispetto al valore desiderato, e
si calcola un delta del neurone che serve poi per modificare i diversi pesi
Il delta del neurone Y si calcola moltiplicando l'errore per la derivata della
funzione di uscita (Y*(1-Y)), in questo modo il delta rappresenta in un certo
senso la velocita' di variazione dell'errore del neurone al variare complessivo
dell'attivazione interna, definita come la somma pesata di tutti i segnali in
ingresso
I pesi vengono modificati di una quantità pari al delta del neurone per il
segnale in arrivo su quella connessione e il tutto ancora moltiplicato per un
fattore h detto fattore di apprendimento (compreso tra 0,1 e 0,9) scelto a
priori. Maggiore è h più rapida è la variazione dei pesi durante
l'addestramento, ma questo puo portare ad errori eccessivi e oscillazioni
nell'apprendimento. Un h basso permette un addestramento più preciso ma
più lento e rischi di minimo locale della funzione di errore
Nel caso in cui il neurone da addestrare appartenga ad uno strato
intermedio non e' possibile determinare il suo errore come
differenza tra l'uscita voluta e quella effettiva, in questo caso si
usa "retropropagare" l'errore che era stato calcolato sull'uscita
effettiva attraverso il delta
L'errore del neurone H (hidden) viene considerato pari al delta del
neurone successivo moltiplicato per il peso della connessione che
unisce i due neuroni
Nel caso in cui la sua uscita andasse verso piu'neuroni, l'errore
sarebbe la somma di tutti i singoli delta pesati
Una volta determinato l'errore di H e' possibile calcolare il DeltaH
ed effettuare le variazioni dei pesi nello stesso modo di prima
N.B. Per il calcolo dell'errore si parte dall'uscita e si procede
verso gli ingressi (calcolando il delta di tutti i neuroni della rete
PRIMA di iniziare a modificare i pesi)
L'algoritmo di backpropagation può quindi essere diviso in due
passi:
Forward pass: l'input dato alla rete è propagato al livello
successivo e così via ai livelli successivi (il flusso di informazioni si
sposta in avanti, cioè forward). Si calcola dunque E(w), l'errore
commesso.
Backward pass: L'errore fatto dalla rete è propagato all'indietro
(backward) e i pesi sono aggiornati in maniera appropriata
Molto schematicamente:
1.Si impostano i pesi a piccoli valori casuali
2.Per ogni esempio
a) Si presenta l'esempio alla rete e la si esegue per
determinarne l'uscita
b) Si calcolano i delta di tutte le unita'
c) Si modificano i pesi
3.Se il massimo errore commesso da una qualsiasi
unita'di uscita durante un qualsiasi esempio e'
maggiore di quello ammesso torna al punto 2
Un esempio
(da G.Ferrari-Trecate,
http://sisdin.unipv.it/lab/didattica/corsi/imad_laurea_PV/reti_neurali1.pdf)
Problemi della backpropagation
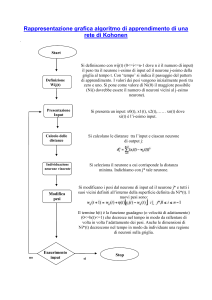
Self-Organizing Map
Le Self-Organizing Map (SOM) sono un particolare tipo di
rete neurale artificiale, con apprendimento non
supervisionato
Producono una rappresentazione dell’informazione in uno
spazio bidimensionale preservando le proprietà
topologiche dello spazio degli ingressi
Questa proprietà rende le SOM particolarmente utili per la
visualizzazione di dati di dimensione elevata. Il modello
fu inizialmente descritto dal finlandese Teuvo Kohonen,
negli anni Ottanta, per cui vengono anche chiamate
Mappe di Kohonen
Le self-organizing map sono reti neurali
Feedforward a singolo strato dove i neuroni di
uscita sono organizzati in griglie di bassa
dimensione (generalmente 2D o 3D). Ogni ingresso
è connesso a tutti i neuroni di uscita. A ogni
neurone è associato un vettore dei pesi della
stessa dimensione dei vettori d'ingresso. La
dimensione del vettore d'ingresso è generalmente
molto più alta della dimensione della griglia di
uscita. Le SOM sono principalmente usate per la
riduzione della dimensione piuttosto che per
l'espansione
Dato che nella fase di addestramento i pesi di tutto il
vicinato sono spostati nella stessa direzione, elementi
simili tendono ad eccitare neuroni adiacenti. Perciò le
SOM formano una mappa semantica dove campioni
simili vengono mappati vicini e dissimili distanti
Un altro modo di considerare i pesi neuronali è di
pensarli come punti distribuiti nello spazio degli
ingressi. Questi formano un'approssimazione della
distribuzione dei campioni d'ingresso. Più neuroni
puntano a regioni con un'elevata concentrazione di
campioni di addestramento, e meno in zone dove i
campioni sono scarsi