m1
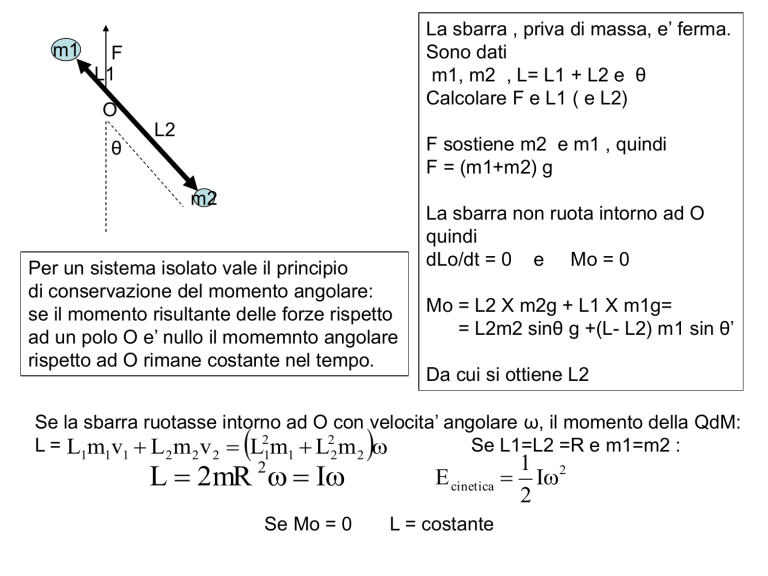
La sbarra , priva di massa, e’ ferma.
Sono dati
m1, m2 , L= L1 + L2 e θ
Calcolare F e L1 ( e L2)
F
L1
O
θ
L2
F sostiene m2 e m1 , quindi
F = (m1+m2) g
m2
Per un sistema isolato vale il principio
di conservazione del momento angolare:
se il momento risultante delle forze rispetto
ad un polo O e’ nullo il momemnto angolare
rispetto ad O rimane costante nel tempo.
La sbarra non ruota intorno ad O
quindi
dLo/dt = 0 e Mo = 0
Mo = L2 X m2g + L1 X m1g=
= L2m2 sinθ g +(L- L2) m1 sin θ’
Da cui si ottiene L2
Se la sbarra ruotasse intorno ad O con velocita’ angolare ω, il momento della QdM:
L = L1m1v1 L 2 m 2 v 2 L21m1 L22 m 2
Se L1=L2 =R e m1=m2 :
L 2mR 2 I
Se Mo = 0
E cinetica
L = costante
1 2
I
2
Archimede e’ famoso per la frase “datemi un punto d’appoggio e sollevero’
Il mondo” .
Data una forza F ed un punto O nello spazio si puo’ definire il prodotto
vettoriale M= R X F = momento della forza F rispetto al polo O.
Un momento produce una rotazione:
data la leva L (di massa nulla) con fulcro in O e le due masse m1 e m2
Archimede trova che si ha equilibrio (assenza di moto) se
d2Xm2g + d1Xm1g = 0
d2
b) d2X m2g = (r2 – L) X m2g
O
m2g
r2
a) d1X m1g = ( r1 –L)X m1g
d1
m1 g
L
r1
La somma a+b deve dare zero
r1Xm1g + r2Xm2g = (m1+m2) LXg
(m1r1 + m2r2)Xg = (m1 + m2) LXg
L(m1+m2) = m1r1 + m2r2
L = (m1r1 +m2r2) / (m1+ m2)
L e’ il raggio vettore di O che viene chiamato Centro di Massa o “baricentro”
= centro dei pesi. Nel caso di n masse L cm mi ri / imi
i
O e’ il punto sul quale il vincolo esercita la forza (m1+m2)g in modo che
la leva non ruoti (cioe’ sia in equilibrio). Da qui il nome “centro di massa”
Dinamica dei sistemi
consideriamo un sistema di N punti materiali, indichiamo con:
Pi il punto i-esimo
mi la massa del punto i-esimo
Fi(t) la forza agente sul punti i-esimo all'istante t
la forza Fi che agisce su un certo punto ad un certo istante è
dovuta alla interazione del punto con gli altri punti materiali
e del punto con corpi esterni:
forza interna: ogni forza esercitata sopra un punto del sistema da un altro punto del
sistema stesso
per distinguere il contributo delle forze
indichiamo con
Fi,j forza di Pj su Pi
FiI la risultante delle forze interne agenti sul
punto i-esimo
FiE la risultante delle forze esterne agenti sul
punto i-esimo
la forza totale agente sul punto i-esimo sarà
allora:
Fi
I
N
F
j1( j i )
i, j
Fi FiI FiE
Forze interne ed esterne
se consideriamo la forza che il punto Pi esercita sul punto Pj, dal principio di
azione-reazione ricaviamo che
Fi , j Fj,i
otteniamo:
FI
i
N
I
F
F
ij i i 0
j1( j1)
ad ogni istante la risultante di tutte le forze interne agenti in un sistema
materiale è nulla
Fi FiI FiE mi a i
l'equazione del moto del punto Pi è:
Che dipende dalle forze interne ed esterne
agenti su i.
Sommando su tutti gli indici i si ha
I
E
E
E
F
F
F
F
F
mi a i
i i i i
i
i
i
i
i
Dinamica dei sistemi
Qi = mi v i
è la quantità di moto del punto Pi,
la somma
Q mi vi
i
d
d
m
r
i 1 dt MR cm MVcm Qcm
dt i
viene chiamata quantità di moto totale del sistema, essa e’ uguale
alla Quantita’ di moto del Centro di massa del sistema.
Si puo’ allora scrivere
FE
d
d
d
m
v
q
i i dt i i dt Qcm
dt i
ad ogni istante la risultante di tutte le forze esterne agenti su un
sistema materiale è uguale alla derivata rispetto al tempo della quantità
di moto totale del sistema
la quantità di moto totale di un sistema materiale isolato è
costante nel tempo
Teorema del moto del centro di massa:
il centro di massa di un sistema materiale si muove come un punto materiale di massa
uguale alla massa totale del sistema e soggetto ad una forza uguale alla risultante delle
forze esterne agenti sopra il sistema
Si immagini un insieme di n masse mi nello spazio : su di ognuna di esse
agisce la forza di gravita’ dovuta alla terra, FORZA ESTERNA,
ma anche la forza di gravita’ reciproca fra le masse.FORZE INTERNE
Le masse acquisteranno tutte una stessa accelerazione verso la terra .
ed una accelerazione le une verso le altre dovuta alla mutua attrazione.
A causa della forza esterna
dQi/dt = G mi Mt/r2 (assumendo che le
dimensioni del sistema di n masse sia piccolo rispetto a r )
dQ/dt = Σ dQi/dt = G Mt/r2 x Σ mi = FE
notare che Σ mi e’ la massa totale.
Poiche’ le attrazioni interne a due a due sono eguali e opposte , eguali
e opposte sono le variazioni delle loro QdM , la cui somma totale e’ quindi
nulla .
In conclusione il sistema ha un moto collettivo verso la terra la cui
QdM varia secondo la
dQ/dt = Σ DQi/dt = G Mt/r2 x Σ mi diversa da zero ,
e un moto indipendente di contrazione dovuto alla mutua interazione per cui
la somma vettoriale delle DQij /dt e’ nulla.
Il moto delle masse mi consiste di un moto collettivo durante il quale il CM si muove
come se su di esso fosse applicata la risultante delle forze esterne. Piu’ un moto
relativo al CM. In un corpo rigido questo puo’ essere solo una rotazione .
Poiche’ il momento delle forze interne rispetto al CM e’ zero ( per definizione la retta
d’azione di una forza di scambio passa per il CM dei due punti che si scambiano) la
condizione di non rotazione da’ che Mcm delle forze ext.=0
a) Non c’e’ attrito : scende con acc. a =gsinθ
Ma cade indietro a causa del momento rispetto al CM
della reazione Vincolare normale. La posizione di
Equilibrio e’ quella per cui CM e’ sulla normale al pendio
a
b
Caso tipico
dello sciatore
b) c’e’ attrito, l’accelerazione e’ minore o nulla , il
Momento dell’attrito Fa tende a provocare una rotazione
in avanti. La persona dovra’ spostarsi leggermente
indietro in modo che il momento della reazione normale
equilibri quello dell’attrito.Cioe’ che Rn +Fa passi per CM.
Poiche’ l’attrito e’ (μ Rn) il rapporto tra Fa e Rn e’ μ.
L’angolo di arretramento rispetto alla normale al terreno
e’ tang θ’ = μ Se μ = 0,1 si ha θ’ ~ 6 gradi.
Su ghiaccio disperatamente in avanti, su neve fresca
o molle un po’ indietro.( ma sempre avanti rispetto alla
verticale g)
Un caso importante e’ il moto geenrato da una forza centrale come la gravita’:
Un oianeta descrive un’orbita circoalre o ellittica intorno al sole.
La forza e’ sempred diretta verso il sole : il suo momento rispetto al sole e’ nullo.
Ne segue che il momento della quantita’ di moto rispetto al sole e’ costante.
s
θ
P1
P2
r
O
L’area di OP1P2 e’
A ~ ½ r s sinθ = ½ r X s
dA/dt = ½ dr/dt X s + ½ r X ds/dt = ½ r X v
perche’ dr/dt = v che e’ parallelo a s
Lo = r x q = r x mv = costante perche’ Mo = 0 (la forza passa per o)
Lo = 2m dA/dt
quindi se Lo e’ costante lo e’ anche la velocita’ areale
Impulso
Per una forza costante F si definisce come IMPULSO I (t1,t2) della forza tra t1 e t2
come il prodotto della forza per il tempo in cui ha agito
I (t1,t2) = F Δ t
dI = F dt = m dv/dt dt = m dv
L’impulso e’ un vettore che ha la stessa direzione della Forza e si misura in N sec.
Se la forza non e’ costante l’impulso e’ dato dall’integrale
t2
t2
t1
t1
I( t1 , t 2 ) Fdt m d v
I( t1, t 2 ) m(V( t 2 ) V( t1 )) q( t 2 ) q( t1 )
La somma degli impulsi di tutte le forze agenti su un punto materiale e’ uguale
all’impulso della forza risultante.
Teorema dell'impulso: l'impulso di una forza in un certo intervallo di
tempo è uguale alla variazione, in quell'intervallo di tempo, della
quantità di moto del corpo sul quale agisce la forza
Urto = scambio di impulsi
L’urto puo’ essere ELASTICO = forza elastica (molla) conservativa
si conserva l’energia meccanica E = U+ Ek
L’urto puo’ essere parzialmente o totalmente ANELASTICO : E non si conserva
Forze interne = Σij Fij = 0 lo stesso vale per gli impulsi
Q = q1 +q2 = costante la quantita’ di moto si conserva SEMPRE !!!
Σij Fij = 0
'
'
dQ=0
Q iniz = m1V1 m1V1 m 2 V2 = Qfin
Se l’urto e’ elastico :
Lavoro = Uf + Ekf – (Ui + Eki) = 0
Le biglie si sono compresse e ridistese Uf = Ui
1
1
1
'2
'2
m1V1 m 2 V2 m1V12 0
variaz. E cin=
2
2
2
U1 e U2 V iniziali
v1 e v2 le V finali
m1v1 + m2v2 = m1u1 + m2u2
½ m1 v12 +1/2m2v22 = ½ m1u12 +1/2 m2 u22
m1 ( u1-v1) = - m2 (u2-v2)
m1 (u12-v12) = - m2(u22-v22)
U1+v1=u2+v2
v1-v2 = -(u1-u2)
V1 = (m1u1+m2u2- e m2(u1-u2))/(m1+m2)
V2= (m1u1 +m2u2 + e m2(u1-u2))/(m1+m2)
e= 1
urto elastico
e= 0 totalmente inelastico
m1v1 = m1v1’ + m2v2’
½ m1 v12 = ½ m1 v1’2 + 1/2m2v2’2
Dalla 1 si ha v’2 = m1/m2 ( v1-v1’)
All’aumentare di m2 v’2 diminuisce e
V’1 a V1
½ m2 v’22 tende a zero
Assumendo le masse uguali e sostituendo v2’ = v1- v1’ si ha v1’= 0
Se m2 tende a infinito v’2 tende a zero
non si ha conservazione di q ma solo dL = dEk
Cioe’
½ mv1’2 – 1/2mv12 = 0
e quindi v1’ = -v1
Nel caso non perpendicolare si vara’ che la componente di q parallela
alla parete si conserva e quella perp. No
L’impulso sulla parete = 2q l’impulso DALLA parete = - 2q
Pendolo balistico
M= sacco pesante, m proiettile di fucile con velocita’ v, che vi
si conficca e arresta. Sia M=5 Kg, m= 15 gr , H= 40 mm
Calcolare la v del proiettile.
L
H
M
v
m
Vi sono due forze esterne ,la gravita’ e la tensione,
entrambe agiscono lungo L
L’atto di moto iniziale e’ pero’ tangente al cerchio
di raggio L , quindi il loro lavoro, anche impulsivo,
e’ nullo. Le sole forze agenti,impulsivamente, sono
Interne e frenano il proiettile nel tempo dT.
La quantita’ di moto si conserva , l’energia no a causa
dell’attrito sacco proiettile.
(M+m)V = mv
V = mv/(m+M)
Dopo l’istante dell’urto agiscono la sola gravita’ e la Tensione. Si conserva l’energia
meccanica. Quando (M+m) raggiunge la max elongazione, la sua Velocita’ e’ nulla
e si e’ sollevato di H .
(M+m)V2/2 = (M+m) gH = (m+M) m2v2/(m+M)2/2 = [(m/(m+M)] mv2/2
H e’ quindi proporzionale all’energia cinetica del proiettile.
v2=2[(m+M)/m]2 g H
Notare che l’energia cinetica finale e’ m/(m+M) Ek iniziale.
(dispositivi analoghi sono usati dai giostrai per misurare l’intensita’ dell’impulso
di un pugno o di un calcio. In elettronica m e’ un impulso brevissimo di corrente I e
M e’ un circuito RC con costante di tempo molto lunga, la tensione finale raggiunta
Ai capi del condensatore e; proporzionale a alla carca I dt portata dall’impulso.
v
S
V = costante
Resistenza dell’aria?
Dimensionalmente : massa auto,densita’aria,
Sezione frontale,velocita’, forma……..
F ~ ρ S V2
Nel tempo T avanza di X = VT spazzando il volume SVT e spostando
Una massa di aria M = ρ SVT = ρ SX.
L’aria deve essere spinta di lato di un tratto <Y> ~ k S1/2 nel Tempo T=x/V
La velocita’
<y>/T = k S1/2 V/x e l’energia cinetica
Ek = ½ ρ SX k2 S V2 /X2 = ½ ρ S k2 S V2 /X
Moltiplicando e dividendo per X
Ek = ½ ρ S V2 Cx X
Dove Cx = k2 S/X2 e’ un a quantita’ adimensionale che dipende dalla forma
Ek e’ energia cinetica dissipata = lavoro della Fattrito per percorrere X =
Lavoro fatto dal motore per mantenere la V costante
Ek = Fa X
e quindi
Fa = ½ ρ S V2 Cx
[ m l2 l2 /l3 t2] = [mlt-2]
La potenza e’ lavoro nell’unita’ di tempo = Ek/T = F v = ½ ρ S V3 Cx
y
a
x
F
dX
θ1
x
F
a e’ una perturbazione che si propaga
Lungo la corda. Sia Y= Y(x) la sua
Forma. F e’ la tensione ai capi di dx.
Il moto di dx e’ lungo Y sotto l’azione
θ2 Della forza
Fy = F ( sinθ2- sin θ1)~ F( tg θ2- tg θ1)
tg θ2 = dY/dx (x=x+dx) e tg θ1= dY/dx (x=x)
( tg θ2- tg θ1) = d2Y/dx2 dx
Fy = F d2Y/dx2 dx = “may” = ρ dx d2Y/dt2
d2Y/dx2 = ρ/F d2Y/dt2
Questa equazione ha soluzioni del tipo f = f (X)= f (wt – kx) e rappresenta
Un’onda che si propaga . Infatti il valore f (0) per X = 0 si ottiene per tutte
Le copie (x,t) che soddisfano la condizione wt-kx=0 cioe’ x = w/k t
Dove V= w/k e’ la velocita’ di “propagazione” della “forma” f.
Si noti che [w] = [t-1] e [k]=[x-1] quindi w rappresenta una frequenza e t una
Lunghezza (d’onda o altro).
Poiche’ d2f/dx2 = k2 d2f/dX2 e d2f/dt2 = W2 d2f/dX2 l’equazione e’ anche
d2f/dx2 = (k/w)2 d2f/dt2
e
V2 = ρ/F
Su una corda tesa e inestensile: gli unici parametri fisici sembrano essere la densita’ lineare λ della
corda e la sua tensione T (la lunghezza e’ ininfluente e supposta infinita, la gravita trascurabile (cioe’
la tensione e’ >> λg)
[λ] = m/l
[T] = ml/t2
[v2] = T/λ
Tensioni elevate o λ piccole = v alta = frequenza elevata o lungh. d’onda corta.
Masse elevata o T bassa = frequenze basse o lungh. d’onda lunga
In un fluido incomprimibile (es. acqua) : l’ampiezza A , ρ, la lunghezza d’onda L, g …………
l’ampiezza A potrebbe essere importante, ma probabilmente e’ A/h (profondita’) che e’ importante e
se h >>A l’ampiezza dovrebbe essere irrilevante.
A parita’ di ρ la velocita’ sara’ v2 ~ Lg cioe’ w/k = L1/2/g1/2 l’onda lunga e’ piu’ veloce.
L’onda si disperde perche’ le alte frequenze corrono meno ,rimangono indietro…….
Se pero’ A diventasse importante (cioe’ A/h non infinitesimo) si potrebbe ottenere V2 = Ag
E questo e’ interessante perche’ non ci sarebbe dipendenza da L (nessuna dispersione) e l’onda
potrebbe propagarsi con velocita’ elevata dipendente dalla sua ampiezza. (solitoni,onde solitarie e
Tsunami)












