1. Il principio di Huygens

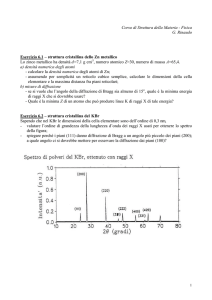
Cap. VI La diffrazione
1. Il Principio di Huygens
2. Teoria di Frauhofer
3. Potere risolutivo angolare
Introduciamo ora:
1. Il principio di Huygens
“Ogni punto del fronte d’onda diviene sorgente di un’onda sferica
secondaria in fase con la primaria”
fronte d’onda
onda piana
Evidenze sperimentali
fronte d’onda
diaframma
la fenditura (foro)
onde sferiche
sorgenti
puntiformi
previsioni dell’
ottica geometrica
onda piana
onde sferiche
la luce non si propaga sempre in linea retta!
diffrazione
il disco
fronte d’onda
disco
opaco
onda piana
ombra
luce al centro
geometrica
del disco d’ombra!
diffrazione
più in generale:
diffrazione ai bordi
luce “oltre” i bordi
ombra d’ombra!
geometrica
ostacolo
diffrazione
2. teoria qualitativa della diffrazione
diaframma
Si consideri la prima
metà della fenditura
D
sin 
2

D
2
P
Le sue estremità daranno:
prima
frangia scura
D
λ
sin  
2
2
altre frange
scure
λ
sin   m
D
schermo
diffrazione
teoria della diffrazione di Frauhofer: L >> D
in P:
diaframma
dE0  adx
L
per il raggio AP:
dE  dE0sin t  adx sin t
per il raggio da dx:
dE  adx sin t  
con:
x sin 
  2
λ
D
2
D
2

dx
x
A
P
quindi in P:

E   dE 
D
2
x sin  

a
sin

t

2

 dx
D 
λ 

2
schermo
diffrazione di Frauhofer
diaframma
L
quindi in P:

E   dE 
D
2
x sin  

a
sin

t

2

 dx
D 
λ 

D
2
2
D
2
è un integrale del tipo:
dx
x
A
P
 a sin( b  cx)dx
la cui soluzione è (Mencuccini-Silvestrini):

sin   

sin

D



λ
 sin t
E (t )  aD 
sin  

D


λ
schermo
sin  

sin  D

λ 
con ampiezza: E0  aD 
sin 
D
λ
diffrazione di Frauhofer
diaframma
L
se l'ampiezza è:
sin  

sin  D

λ 
E0  aD 
sin 
D
λ
D
2
l’intensità sarà:
I 
A
D
2
a D  sin  


2Z   
2
dx
x
2
P
2
schermo
con:
sin 
  D
λ
1.0
I
sin min   m
0.8
0.6
   m  I min
λ
D
0.4
0.2
tg  
 I max
(
)
risoluzione
grafica
0.0

2λ
D

λ
D
0
λ
D
2λ
D
3λ
D
sin
diffrazione
diffrazione
la diffrazione di Frauhofer
fenomenologia
schermo
diaframma
onda
piana
I
otticaondulatoria
geometrica
ottica
D
sin
L
diffrazione di Frauhofer
diaframma
a 2 D 2  sin  
sin 
con:
I 



D


λ
2Z   
2
sin min
λ
 m
D
λ
2sin θ 0  2

D
(
D
2
dx
x
A
D
2
P
)
“larghezza” del
massimo centrale
schermo
1.0
si noti il comportamento per:
λ
 0
D
I
λ
 0
D
0.8
0.6
0.4
0.2
0.0

3λ 2λ
λ


D
D
D
λ
D
2λ
D
3λ
D
sin
diffrazione
diffrazione
la diffrazione di Frauhofer
le dimensione della fenditura
diaframma
onda
piana
diffrazione
diffrazione
a D  sin  
I 


2Z   
2
2
la diffrazione di Frauhofer esempio numerico
schermo
2
Intensità
diaframma
sin 
  D
λ
y 
λ
sin 0 
D
assumendo:
1
2
2λ
D
λ
D

D
0

P
D  0.1 mm
λ  0.5 m
D
 200  sin  0  0.005
λ
Per i massimi, si trova che:
sin θ *  θ *  1.5  θ 0  0.0075
L
   4.7  I '
I max

22

λ
D

2λ
D
diffrazione
disco
opaco
diffrazione
ai bordi
fenditura
diffrazione
diffrazione
a 2 D 2  sin  
I 


2Z   
3. potere risolutivo angolare
2
schermo
diaframma
I
S2

D

S1
2λ
D
potere risolutivo
angolare
se:    R 
λ
D
le sorgenti sono indistinguibili
diffrazione
diffrazione
λ
R 
D
potere risolutivo angolare
di uno strumento ottico
per due stelle lontane è determinante la separazione angolare:
S2
S2
2
1
D
S1
λ
se:    R 
D
le stelle sono indistinguibili
diffrazione
diffrazione
limite diffrattivo per la
collimazione di un fascio
è impossibile ottenere un fascio perfettamente collimato come questo:

2
D
S1

2
è comunque:
λ
   R 
D
Esercizio numerico
5.1 Una luce violetta di lunghezza d’onda  = 415 nm incidendo su una fenditura origina
un picco centrale di diffrazione largo 9.2 cm su uno schermo posto a distanza L = 2.25
m. Qual è l’apertura della fenditura?
diaframma
sin min
λ
 m
D
2λ
D
λ
D

D
λ
2sin θ 0  2

D
(
y0  2Lsinθ0

)
“larghezza” del
massimo centrale
y0  2 L
λ
D
λ
415  109
D  2L
 2  2.25 
 20.3 m
2
y0
9.20  10
0

L

λ
D

2λ
D
Esercizio numerico
5.2 In un esperimento di diffrazione alla Fraunhofer mediante fenditura rettangolare di
apertura D = 30 m, vengono utilizzate due onde monocromatiche di lunghezza d’onda
1 = 6000 Å e 2 = 5000 Å. Determinare il valore minimo di  per cui si ha
sovrapposizione di due frange scure.
1
2
D

Esercizio numerico
1 2
sin min
λ
 m
D
D sin   λ1m1
D
λ1m1  λ 2m2
D sin   λ 2m2

λ2
5
m1 
m2  m2
λ1
6
Il primo minimo si ha per:
m1  5
m2  6
min  5.74
sin min
λ1
λ1
6000  1010

m1  5  5
 0.1
6
D
D
30  10
Esercizio numerico
5.3 Si calcoli la minima dimensione  che deve avere un cratere sulla luna perché possa
essere visibile (“risolto”) con un telescopio il cui obiettivo ha un diametro D = 60 cm,
assumendo per la distanza Terra-Luna il valore l = 380.000 km e che la risoluzione sia
solo limitata dalla diffrazione.


D
l
se:
λ
   R 
D

λ
 

l
D
le diverse parti del cratere sono indistinguibili

-7
λ min
8 4  10
  l
 3.8  10
 253 m
D
0.6