Document

Il teorema dell’impulso
• Consideriamo un punto materiale in moto rettilinio sotto
l’azione di una forza F costante
O
• xo punto di partenza
• x punto di arrivo
x
x
xo F
x  x  x o
t  t  t o  t  0
spostamento
Tempo impiegato
• L’accelerazione (costante) a x  F
m
• Le equazioni del moto
x  x o  vx ot  12 a xt 2
v x  vx o  a x t
mv x  mv x o  ma x t  p x f  p x f  Ft  0 

px  Ft
G.M. - Edile A 2002/03
Generalizzazione del teorema
dell’impulso
• Dalla seconda legge della dinamica
• Dove F è la risultante delle forze agenti sulla particella
dp
F
dt
dp  F dt
• Per ogni intervallo infinitesimo dt
• Sommando su tutti gli intervalli infinitesimi (integrando
tra zero r t)
t
t
0
0
 dp   Fdt


t
p  Fdt
0
• Se la forza F è costante (modulo, direzione e verso)
• La forza F media in t


t
p  F dt  Ft
0
t
Fdt
p
Fm 
 0
t
t
G.M. - Edile A 2002/03
Lavoro ed energia cinetica: introduzione
• Consideriamo un punto materiale che si muove di moto rettilineo sotto
l’azione di una forza costante parallela alla traiettoria (per esempio
moto di caduta di un grave)
O
x
F
F  ma  F  ma x
ax 
x  x o  vx ot  12 a xt 2
Eliminando il tempo:
vx  v xo
ax
x  x o  vxo
vx  v xo 1 
v  vxo 

 2 a x  x
ax
 a x 
Moto uniformemente
accelerato
2vxo vx  2vxo vxo  v 2x  v2xo  2vxo vx v 2x  v2xo
x  xo 

2a x
2a x
v x  vx o  a x t
t
F
 cos tan te
m
2
v 2x v2x o

 a x x  x o 
2
2
1
1
2
2
mv x  mv x o  ma x x  x o 
G.M. - Edile A 2002/03
2
2
Lavoro ed energia cinetica: introduzione
1
1
2
2
mv x  mv x o  ma x x  x o 
2
2
1
1
2
2
mv x  mv xo  Fx  xo 
2
2
• Si definisce
• Energia cinetica della particella
1 2 1 2
K  mv x  mv
2
2
• Lavoro effettuato dalla forza costante sul percorso tra xo e x
W  Fx  xo 
Le dimensioni
W  F L
2
K  M v
Nel SI: Nm=kgm2s-2=J (joule)
Nel SI: kgm2s-2=J (joule)
G.M. - Edile A 2002/03
Generalizzazione della definizione di
lavoro
• Nello studio del moto rettilineo uniformemente accelerato abbiamo
ottenuto:
– La variazione dell’energia cinetica dubita dal punto materiale
quando si sposta tra xo e x risulta uguale al lavoro compiuto dalla
forza lungo il percorso tra xo e x
– Teorema delle forze vive.
• Vediamo se è possibile generalizzare questo risultato al caso generale.
– Se la traiettoria non è rettilinea o se la forza non è parallela allo
spostamento, solo la componente tangenziale della forza è responsabile
della variazione del modulo della velocità:
dv
Ft
 at 
dt
m
Occorre fare in modo, nella definizione di
lavoro di una forza, che esso dipenda solo
dalla componente tangenziale della forza.
F
Ft  Fcos
r
G.M. - Edile A 2002/03
Il prodotto scalare tra vettori
• Dati vettori F e r, si definisce prodotto scalare
F
Il risultato di un prodotto
F  r  Fr cos  scalare è uno scalare

F  r  r  F Commutativo
r
• Modulo del primo vettore per modulo del secondo vettore per il coseno
dell’angolo compreso
• Che può anche essere interpretato come
– Il modulo del primo vettore per la proiezione del secondo vettore
lungo il primo
F  r  Fr cos 
F
r cos

r
– Il modulo del secondo vettore per la proiezione del primo sul
secondo
F
F cos
F  r  rF cos 

r
G.M. - Edile A 2002/03
Alcune proprietà del prodotto scalare
• Vettori paralleli
– Positivo Fr
• Vettori antiparalleli
– Negativo - Fr
• Vettori ortogonali
F
r
F
r
F
– Uguale a zero
r
i i 1
j j 1
i  j  i  k  j k  0
k k  1
F  Fx i  Fy j  Fzk
r  xi  yj  zk
Il prodotto scalare di un
vettore per sé stesso
aa  a
2
F  r  Fx x  Fy y  Fzz
G.M. - Edile A 2002/03
Generalizzazione della definizione di
lavoro
• Lavoro fatto da una forza costante su un percorso rettilineo
F

W  F  r  Frcos 
r
Il lavoro è una grandezza scalare
• Se la forza non è costante e/o il percorso non è rettilineo, possiamo
sempre
– dividere il percorso in tratti così piccoli (infinitesimi) da poter considerare
• il tratto rettilineo e
• la forza costante su quel tratto,
– Calcolare il lavoro su ciascuno dei tratti
– Sommare tutti i lavori calcolati sui singoli tratti
W
dW  F dr
f
 F  dr
i,

f
i
G.M. - Edile A 2002/03
Generalizzazione della definizione di
lavoro
• Calcolo del lavoro utilizzando le componenti cartesiane
F  Fx i  Fy j  Fz k
W
dr  dxi  dyj  dzk
 F  dr   F dx  F dy  F dz
f
f
i,
i, 
x
y
z
• Calcolo del lavoro utilizzando i moduli della forza e dello spostamento
dr  ds modulo di dr
W
f
f
i,
i, 
 F  dr   Fdscos
• I lavoro della risultante

n
R

F
i
i
i1

f
WR  R dr 
i, 
f
F
n
n
n
 F  dr    F  dr   W
f
i,
i
i1
i1
f
i,
i
i
i1
G.M. - Edile A 2002/03
• Una donna tira, a velocità costante, una slitta carica di massa m= 75 kg su
una superficie orizzontale. Il coefficiente di attrito dinamico tra i pattini e
Applicazi
la neve è md=0.10, e l’angolo f è di 42°.
one
• Calcolare il lavoro effettuato dalla donna per spostare la slitta di 10 m.
• Calcolare il lavoro fatto dalla risultante delle forze
La forza applicata dalla donna è uguale alla
tensione T (possiamo calcolare il lavoro della
tensione T).
Il lavoro effettuato dalla donna sarà:
T
f
r
W  T  r  Trcos f
Forza costante
Spostamento rettilineo
Bisogna calcolare il modulo di T.
N  Fg  T  fk  ma
x : T cos f  fk  ma x  0
y : N  T sen f  mg  ma y  0
G.M. - Edile A 2002/03
x : T cosf  md N  0
y : N  T sen f  mg  0
T cos f  m d (mg  T sen f)  0
T cos f  m d senf   m d mg
N  mg  Tsenf
T
Applicazi
one
m dmg
 90.8 N
cos f  m d sen f
costante
N  mg  T senf  75kg 9.81
m
2  91N sen 42  675 N
s
fk  m d N  0.10  675 N  67.5 N
Il lavoro effettuato dalla donna (dalla tensione):
WT  Trcos f 
md mg
r cos f  90.8 N *10m * cos 42  675 J
cos f  m d sen f
Wfk  fk rcos  67.510  1  675J
WN  Nr cos   675 10  0   0J
WFg  Fg r cos   735.710  0  0J
WR  WFg  WN  WT  Wfk  0  0  675  675  0J
G.M. - Edile A 2002/03
Potenza
• Data un forza esegue un lavoro W in un intervallo di tempo t
• si definisce potenza media nell’intervallo t il rapporto :
Pmedia 
W
t
• La Potenza sviluppata dalla forza all’istante t (potenza istantanea), si
ottiene facendo il limite per t che tende a zero:
dW  F dr  F  vdt
dW
P
dt
dW F  dr
dr
P

 F
 Fv
dt
dt
dt
Le dimensioni [P] = [ML2T-2][T-1] = [ML2T-3]
Nel SI si misura in watt (W)
Altre unità cavallo vapore (Cv)
Kilovattora come unità di
misura del lavoro
1kwattora=3.6MJ
G.M. - Edile A 2002/03
Generalizzazione del
teorema delle forze vive
• Consideriamo il generico intervallo di tempo dt
– La variazione dell’energia cinetica


f
F
i
 
1
1 2  1
2
dK  d mv  m d v  m dv v  
2
 2
2
1
1
 m dv  v  v  dv  m2v  dv  mv  adt  vdt ma  dr  ma 
2
2
 dr  ma  dr  R  dWR
• La relazione vale per tutti gli intervalli infinitesimi: quindi anche
quando si somma su tutti gli intervalli. K  W
R
• La variazione di energia cinetica è uguale al lavoro della risultante
(la somma dei lavori fatto da tutte le forze agenti sul punto materiale)
G.M. - Edile A 2002/03
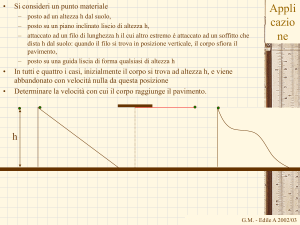
• Un sollevatore di pesi solleva un manubrio di massa complessiva
m=260kg per un dislivello di 2 m
Applicazi
• Determinare il lavoro fatto dalla forza peso durante il sollevamento
one
• Determinare il lavoro fatto dal sollevatore di peso.
Fs
• Se il sollevatore abbandona l’attrezzo mentre è in alto (h=2m) determinare
la velocità con cui arriva sul pavimento.
WP  P  r  mgh cos180  260kg9.81ms 2m1  5200J
2
P
Osserviamo che l’energia cinetica iniziale è nulla, ma anche quella finale.
La variazione di energia cinetica è nulla.
K  K f  Ki  0
Utilizzando il teorema delle forze vive:
K  WR  WP  WFs  0
WFs  WP  5200J
Per quanto riguarda l’ultima domanda: osserviamo che il moto avviene
sotto l’azione della sola forza peso.
Il lavoro fatto dalla forza peso in questo caso:
WP  P  r  mgh cos 0  260kg9.81ms 2m1  5200J
2
K  K f  Ki  WR  WP
vf 
2WP

m
2mgh
m
 2gh  6.26
m
s
K f  K i  WP
1
2
mv
f
2
0J
G.M. - Edile A 2002/03
L’energia
• È una grandezza che caratterizza il punto materiale
– Dipende dal suo stato (posizione, velocità, temperatura, etc)
– Esistono varia forme di energia
– Per es. l’energia cinetica dipende dallo stato di moto del corpo
• I corpi possono scambiarsi l’energia:
– Il lavoro rappresenta un modo attraverso cui i corpi si scambiano energia.
– Se la risultante delle forze esterne compie un lavoro positivo (forza
motrice, concorde con il moto), allora l’energia cinetica del punto
materiale aumenta.
• Si dice che l’ambiente esterno ha compiuto un lavoro sul punto materiale
• il punto materiale ha acquisito energia cinetica dall’ambiente esterno.
– Se la risultante delle forze esterne compie un lavoro negativo (forza
resistente, opposta al moto), allora la sua energia cinetica diminuisce.
• si dice che il punto materiale ha effettuato del lavoro sull’ambiente esterno
• a spese della sua energia cinetica
• L’energia cinetica rappresenta la capacità di un corpo a compiere del
lavoro
– Trasferire cioè il movimento ad altri corpi.
• La corrente del fiume che fa muovere le macine di un mulino
G.M. - Edile A 2002/03
L’energia cinetica
e i sistemi di riferimento
• Il valore dell’energia cinetica, come quella di altre
grandezze dipende dal sistema di riferimento usato.
• Anche le distanze percorse dipendono dal sistema di
riferimento usato
y'
y
r
O
• Ma anche se i valori numerici cambiano, la eguaglianza
tra il lavoro fatto dalla risultante e la variazione
dell’energia cinetica risulta valida in tutti i sistemi di
riferimento inerziali.
z
z
r'
O'
xx'
z'
x  x'  vx O' t
y  y'
z  z'
v x  v' x' vx O'
v y  v' y'
v z  v' z'
G.M. - Edile A 2002/03
• Un oggetto di massa m=10 kg viene portato in un treno dalla velocità
nulla alla velocità di 2 m/s percorrendo (sul treno) un tratto di 5 m. Il
treno si muove con una velocità di 20 m/s rispetto al marciapiede della
stazione. Verificare il teorema delle forze vive rispetto al treno e rispetto
al marciapiede.
2
2
y'
y
v'
v'
4
m
f
i
2
2
a' 

 0.4 2
v' f v' i  2a' (x' f  x' i )
2(x' f x' i ) 2  5
s
m
R  ma '  10kg 0.4 2  4.0N t  v' f v' i  2  5s
s
a'
0.4
1
1
1
m2
2
2
K' f K' i  mv' f  mv' i  10kg  4 2  20J
2
2
2
s
r
O
z
z


2

1
 m v' i  vo
2
z'
r'
O'
xx'
x  x'  vx O' t
y  y'
W'  Rx'  4.0N 5m  20J
1 2 1 2 1
K f  Ki  mv f  mv i  m v' f  vo
2
2
2
1
1
2
2
K f  Ki  1022  1020  420J
2
2
Applic
azione

2
z  z'
v x  v' x' vx O'
v y  v' y'
v z  v' z'
W  Rx  Rxf  x i   Rx' f vo t  x' i   Rx' f x' i vo t  
W  Rx' f x' i vo t   4(5  20  5)  4 105  420J
G.M. - Edile A 2002/03
Le forze conservative
• Una forza si dice conservativa se
–
il lavoro eseguito dalla forza sul punto materiale P mentre si sposta dalla
posizione P1 alla posizione P2 dipende soltanto dalla posizione iniziale e
dalla posizione finale
– e non dal percorso effettuato, dalla traiettoria seguita per andare da P1 a
P2, ne da alcun altro parametro come la velocità, il tempo impiegato, ecc.
• Allora
– esiste una funzione U della posizione del punto
materiale P,
U(P) = U(x,y,z),
– tale che il lavoro fatto dalla forza conservativa
quando il punto materiale si sposta tra due punti
qualsiasi, P1 e P2, è dato dalla differenza tra i
valori che la funzione U assume nel punto
iniziale P1 meno quello che assume nel punto
finale P2.


P1
W

F
P2
f
F  dr 
i,
 U(P1)  U(P2 )  U
U= energia potenziale
G.M. - Edile A 2002/03
y
La forza peso
B
P1
• Verifichiamo che la forza peso è conservativa:
– Dobbiamo far vedere che per qualunque percorso il lavoro
fatto dalla forza per andare da P1 a P2 è sempre lo stesso
indipendente dal percorso.
WP1AP2  WP1 A  WAP2
– Prendiamo il percorso P1A P2.
WP1A  P  d  mg
P1A cos 0
 mg

P1A
P1A
P2
A
 y1  y2
WP1A  mg y1  y2   mgy 1  mgy 2
WP1AP2  WP1 A  mgy 1  mgy 2
WAP2  P d  mg
AP2
cos

0
2
– Prendiamo ora il percorso P1B P2.
WP1BP 2  WP1B  WBP2  WBP 2  WP1A  mgy 1  mgy 2
G.M. - Edile A 2002/03
y
La forza peso
P
– Prendiamo un qualsiasi percorso tra P1 e P2.
W
W
P2
 P  dr
P  mg j
A
P1, 
dr  dxi  dyj  dzk
P2
P2

P1, 
Pxdx  Pydy  Pz dz 

P1, 
B
P1

dr
P2
P2
 mgdy  mg dy 
P1, 
W  mg yy 2  mgy 2  mgy 1
y
1
• L’energia potenziale potrebbe essere
U  mgy
W  U(P1 )  U(P2 )  mgy 1  mgy 2
G.M. - Edile A 2002/03
La forza elastica
x2
x1
• Valutiamo il lavoro fatto dalla forza elastica per spostare il corpo dalla
posizione x1 a x2.
– Lo spostamento è rettilineo
– ma la forza non è costante
• Utilizziamo la definizione più generale
P2
F
W
W
el
P1, 

x2
x1 ,
 dr
Felxdx  Felydy  Felz dz 
x2
x 
1 2 1 2
W  k
  kx 2  kx1


2
2
 2 x1
2
Fel   kxi
dr  dxi  dyj  dzk

x2
x1, 

x2
 kxdx  k xdx 
x1 ,
Il lavoro dipende solo dai
punti iniziali e finali: la forza
1 2
elastica è conservativa!
U  kx
La sua energia potenziale: G.M. - Edile A 2002/03
2
L’energia potenziale
• E’ un’altra forma di energia, legata la posizione di un corpo
– È possibile cambiare l’energia potenziale di un corpo eseguendo
del lavoro (per esempio sollevare un peso U=mgy)
• le forze conservative
– Forza peso
Ux, y, z  mgy  mgh
– Forza elastica
U(x, y,z) 
1 2
kx
2
Ux, y, z  
– Forza di gravitazione universale
– Forza di Coulomb
h = quota
Ux, y, z 
GmM
r
1 q1q 2
4 o r
• La funzione energia potenziale è determinata a meno di una costante
arbitraria
U1x,y,z  Ux,y,z   cos tan te
G.M. - Edile A 2002/03
Determinazione dell’energia potenziale
dall’espressione della forza
• Utilizzando la definizione di energia potenziale:
WP1P2  U  U(P1 )  U(P2 )
P
• Che può essere riscritta, considerando i punti Po,
iniziale, e P, il generico punto dello spazio:
WPo P  U  U(Po )  U(P)
• Da cui:

Po
P
U(P )  U(Po )  WPo P  U(Po )  F  dr Non è necessario specificare la
Po
traiettoria
• Per derivare la funzione energia potenziale occorre:
– Fissare arbitrariamente un punto dello spazio Po.
– Assegnare un valore arbitrario all’energia potenziale del punto Po.
– Calcolare il lavoro effettuato dalla forza da Po al generico punto P lungo
una qualsiasi traiettoria che connetta Po con P.
G.M. - Edile A 2002/03
L’energia potenziale
• le forze conservative
– Forza peso
• Il punto di riferimento Po è un punto del piano xz, con y=0 (quota nulla)
• Ai punti del piano orizzontale y=0 si assegna energia potenziale nulla
Ux, y, z  mgy  mgh
– Forza elastica
h = quota
• Il punto di riferimento Po è la posizione dell’estremo libero della molla in
condizioni di molla non deformata, x=0.
• Quando la molla non è deformata, x=0, si assegna energia potenziale nulla
U(x, y,z) 
1 2
kx
2
– Forza di gravitazione universale
– Forza di Coulomb
• Il punto di riferimento Po è il punto all’infinto.
• Al punto all’infinito, si assegna energia potenziale nulla
GmM
Ux, y, z  
r
1 q1q 2
Ux, y, z 
4 o r
G.M. - Edile A 2002/03
Il lavoro effettuato da una forza conservativa
su un percorso chiuso è nullo
• Consideriamo un percorso chiuso
W
P2

P1
 F  dr   F  dr   F  dr
P2 ,  1
P1 , 2
• Le forze conservative dipendono dalla
posizione.
1
P1
F
1
P1
F
P2
2

P2
dWA  F dr  Fdscos 
dWR  F  dr  Fdscos   
dWA  dWR

P2

P1
F  dr   F  dr
P1 ,  1
P 2 , 1
W
P2
P2
P1 , 2
P1 , 1
 F  dr   F  dr   F  dr  0
G.M. - Edile A 2002/03
Lavoro della forza di attrito
• La forza di attrito statico fa lavoro nullo:
– Nel caso di attrito statico, non c’è spostamento: quindi il lavoro è
nullo
– Se il piano di appoggio si sposta rispetto al SdR utilizzato, si
osservi che:
• il piano e l’oggetto poggiato su di esso subiscono lo stesso
spostamento
• Le forze di attrito sono uguali ed opposte (azione e reazione)
• Il lavoro complessivo è nullo
a
• La forza di attrito dinamico fa, sempre, un lavoro negativo:
– Consideriamo un oggetto che viene spostato su di un piano
orizzontale scabro.
G.M. - Edile A 2002/03
Lavoro della forza di attrito dinamico
• Consideriamo un punto materiale che si muove su un piano orizzontale
sulla traiettoria  tra P1 e P2.
Fa
• Il modulo della forza di attrito dinamico è
Fad  m d N  m d mg
costante


P1
P2
• Il lavoro effettuato dalla forza di attrito dinamico
WP1P2 
P1P 2
P2
F
ad  dr
P1,  1

P2
 Fadds cos  
P1,  1
P2
P2
 m mgds  m mg  ds
d
P1 , 1
d
P1 , 1
 md mg
P1P 2
è la lunghezza del tratto di traiettoria percorso
• il lavoro della forza di attrito dinamico non dipende solo dal punto
iniziale e da quello finale, ma anche dalla lunghezza della traiettoria
scelta
• Su un percorso chiuso il lavoro è diverso da zero
• La forza di attrito dinamico non è conservativa
G.M. - Edile A 2002/03
L’energia potenziale in presenza di più
forze conservative
• Il lavoro effettuato da tutte le forze conservative è dato da:
n
W
n
W   U  U
k
k 1
n
U
n

k 1
Uk
k
k 1
k 1
ki
 U k f 
n
n
U  U
ki
k 1
kf
k 1
L’energia potenziale totale è la somma delle
energia potenziali delle singole forze
W  Ui  Uf
G.M. - Edile A 2002/03
La conservazione dell’energia
• Supponiamo di avere un punto materiale che si muove sotto l’azione di
forze conservative.
• Il teorema delle forze vive ci dice che il lavoro della risultante è uguale
alla variazione dell’energia cinetica:
WR  K  K f  Ki
• Poiché tutte le forze sono conservative, il lavoro della risultante può
essere messo in relazione con la variazione di energia potenziale
WR  U  Ui  Uf
U
U
k
• Combinando le due relazioni si ottiene:
K  U
K  U  0
K  U  K f  Ki  U f  Ui  K f  Uf  Ki  Ui  Ef  Ei  0
E  KU
energia meccanica totale
Solo forze conservative: l’energia
meccanica totale si conserva!
G.M. - Edile A 2002/03
Relazione lavoro energia
• Se non tutte le forze sono conservative
– Il lavoro della risultante sarà la somma del lavoro effettuato
• Dalle forze conservative Wc
• Dalle forze non conservative Wnc
WR  Wc  Wn c
WR  K
K  U  Wnc
K  U  Wnc
 K  U  Wnc
Wc  U
E  Wnc
• La variazione dell’energia meccanica totale è uguale al lavoro
effettuato dalle forze non conservative.
• Questa relazione contiene come caso particolare anche la
conservazione dell’energia
–
infatti quando non ci sono forze non conservative Wnc=0
G.M. - Edile A 2002/03
L’energia meccanica totale
• In presenza di forze non conservative l’energia meccanica totale non si
conserva
– La sua variazione è proprio uguale al lavoro delle forze non conservative
• In realtà non bisogna pensare che dell’energia sia andata distrutta o si
sia creata dal nulla, semplicemente c’è stato uno scambio con altre
forme di energia.
–
Nel caso di forze dissipative, attrito dinamico, resistenza passiva, il lavoro
(negativo) di queste forze è accompagnato da un aumento della
temperatura dei corpi interessati
• L’energia meccanica totale diminuisce mentre aumenta l’energia interna dei
corpi (aumento di temperatura)
– Nel caso in cui si ha un aumento dell’energia meccanica totale (per
esempio nelle esplosioni), l’energia interna contenuta nell’esplosivo è
stata trasformata in energia meccanica
• L’esplosivo ha subito una trasformazione chimica.
G.M. - Edile A 2002/03
Un corpo di massa m=1kg è appeso mediante una fune ideale di lunghezza
L=3 m al soffitto del Laboratorio. Determinare il periodo del pendolo
nell’ipotesi che esso venga abbandonato da fermo quando l’angolo formato
dalla fune con la verticale è di 5°. Si supponga che l’ampiezza delle
oscillazioni possa essere considerata piccola. Determinare inoltre il valore
della tensione nella fune quando passa per la posizione verticale.
Poniamoci nel sistema di riferimento del
Laboratorio (inerziale) per poter applicare le
leggi di Newton.
Determiniamo le forze agenti
sull’automobile
• La forza peso
• La Tensione della fune
La posizione del
pendolo può essere
individuata
specificando 
la seconda legge di Newton vale:
Applica
zione

T
P
Il diagramma del corpo libero
P  T  ma
v
Preliminarmente ricordiamo che in un moto circolare antiorario:

v  r
dv dr  d
at 


r  r
dt
dt
dt
G.M. - Edile A 2002/03
N.B.Per evitare complicazioni limitiamoci a considerare la parte di
moto antiorario del pendolo.
Applica
zione
Troviamo le tre equazioni scalari corrispondenti all’equazione
vettoriale. Utilizziamo le direzioni ut ed un mostrate in figura,
ed uz perpendicolare ai primi due.
un
T  mg cos   ma n
ut
mg sen  ma t
uz
0  ma z

Forza di richiamo,
opposta a 
un
T
P
Poiché az=0 è la velocità iniziale è nulla, possiamo
concludere che il moto del pendolo avviene nel piano della
figura.
dove  è
Riscrivendo l’accelerazione tangenziale in a  L
t
l' accelerazione angolare
termini di accelerazione angolare si ottiene:
 mg sen  ma  L  gsen 
d 2
dt
2


g
L
sen 
se è piccolo
sen = 
ut
d2 
 2
dt
d 2
g



2
dt
L
L’accelerazione è proporzionale all’opposto
della posizione: il moto è armonico!
G.M. - Edile A 2002/03
d 2
g
Equazione differenziale del moto armonico con



pulsazione angolare p data da:
dt 2
L
p 
Applica
zione
g
L
La legge oraria è del tipo:

t  Acos  p t  
(t) 

T


d
  A p sen  p t  
dt
ut
P
In cui le costanti A e  vanno determinati sulla base delle condizioni
inizali.
Miraccomando a non confondere la velocità angolare con cui si
muove il pendolo con la pulsazione angolare.
Pur avendo le stesse unità di misura sono completamente diverse:
•
•
un

La pulsazione angolare è una costante
p 
La velocità angolare varia sinusoidalmente. Il pendolo si ferma, =0,
agli estremi dell’oscillazione ed è massima per =0.
g
L
G.M. - Edile A 2002/03
Determiniamo le costanti A e :
Ricordiamo le condizioni iniziali:
t  0s  5
(t  0s)  0
Quindi: 5  A cos
0  A p sen
Applica
zione
sen   0
0

La scelta =0, da una soluzione positiva dell’ampiezza:
La legge oraria diventa dunque:

 g 
 9.81 
5 * 
t 
cos  t  0.087cos 
t  0.087cos 1.81  t rad 
180
 L 
 3 
un
T
ut
P
rad
(t)  .157sen1.81  t  
s 
Abbiamo già verificato che la legge oraria del moto armonico è
periodica con periodo T=
T
2 2  3.14

 3.47s
p
1.81
G.M. - Edile A 2002/03
Per il calcolo della Tensione riprendiamo l’equazione secondo un:
T  mg cos  ma n
Dove an è uguale a:
Applica
zione
v2
an 
 2L
L
Per  = 0 la velocità angolare è massima: pari alla sua
ampiezza. Pertanto
T  mg cos  m 2L

per0
mg  m 2p A2 L  mg  m
g 2
A L  mg (1  A2 )
L
Confrontiamo questa tensione con quella che si ottiene
quando il pendolo è fermo in condizioni di equilibrio:
P  T  0  T  P
In condizioni di equilibrio T=mg ed è verticale: il filo si
dispone lungo la verticale (filo a piombo).
Per =0 la tensione nel caso dinamico è più grande che in
quello statico perché essa oltre ad equilibrare il peso deve
fornire la forza centripeta necessaria per far percorrere al
pendolo una traiettoria circolare!!

un
T ut
P
G.M. - Edile A 2002/03