Giulio Tagliavini – Massimo Regalli
Corso di Economia
degli Intermediari Finanziari
La valutazione dei progetti di investimento
Indice
Introduzione
I criteri tradizionali di valutazione dei progetti di investimento;
I criteri finanziari di valutazione dei progetti d’investimento
Alcune definizioni
Cos’è un investimento ?
Gli investimenti sono uscite di cassa, in una o più
soluzioni (fase di impianto), che genereranno nuovi
flussi di cassa positivi (fase di esercizio);
La definizione di investimento per la contabilità non è
la stessa in Finanza di impresa:
Si parla di entrate ed uscite, non di costi e di ricavi !
L’obiettivo: individuare la convenienza economica di
un progetto. Può essere un utile aiuto nella scelta:
di un progetto socialmente importante;
fra più progetti “concorrenti”.
Rappresentazione grafica
Flussi (F)
Tempo (t)
Fase di impianto
Fase di esercizio
La valutazione finanziaria
Oltre all’analisi economica si dovrebbe considerare anche il
profilo finanziario. L’analisi finanziaria, in misura più o
meno rilevante, e deve….
... verificare la compatibilità dei flussi dell’investimento con
il profilo di entrate ed uscite aziendali, sia sotto il profilo
dimensionale che temporale.
Progetti economicamente convenienti,
potrebbero non essere finanziariamente
sostenibili
Indice
Introduzione
I criteri tradizionali di valutazione dei progetti d’investimento:
1.
Il tempo di recupero (payback period)
2.
Il rendimento medio contabile (ROI del progetto)
I criteri finanziari di valutazione dei progetti d’investimento.
Il tempo di recupero (payback period)
Il concetto del payback period (PBP) risponde alla
domanda: fra quanto tempo recupererò l’investimento
iniziale ?
Il PBP non è altro che il numero di periodi necessari
affinché i flussi di cassa cumulati eguaglino l’investimento
iniziale;
Si ritiene che maggiore sia il PBP, maggiore sia il rischio
insito nel progetto.
Il tempo di recupero (payback period)
Due esempi
Esempio 1
Anni
0
1
2
3
4
5
6
Flussi di cassa
-10000
1000
2500
3500
4000
4000
3000
Flussi cumulati
-10000
-9000
-6500
-3000
1000
5000
8000
Tra il 3° e
il 4° anno
Esempio 2
A
B
C
D
E
0
- 1.000
- 1.000
- 1.000
- 1.000
- 1.000
1
1.000
600
800
600
400
2
10
300
200
400
600
3
4
100
500
600
600
300
PBP
1
3
2
2
2
Non aiuta
a
decidere!
Il tempo di recupero (payback period)
Difetti:
non considera i flussi conseguiti nei periodi successivi al
PBP;
non considera il valore finanziario del tempo; Superabile
non considera l’ammontare di capitale investito;
è un indicatore di rischio (esposizione temporale), non
di rendimento.
Pregi:
considera i flussi di cassa (almeno dovrebbe!);
facilità di calcolo, uso e comunicazione.
Il tempo di recupero attualizzato
Il PBP attualizzato supera uno dei limiti della versione “più
semplice”, in quanto tiene conto del valore finanziario del
tempo e il costo del capitale: PBP
t
F
t 1
(t )
(1 k ) F0 0
Esempio (tasso di sconto al 10%)
Anni
0
1
2
3
4
5
6
Flussi di cassa Flussi cumulati Flussi attualizzati
-10000
1000
2500
3500
4000
4000
3000
-10000
-9000
-6500
-3000
1000
5000
8000
-10000
909
2066
2630
2732
2484
1693
Flussi cumulativi
attualizzati
-10000
-9091
-7025
-4395
-1663
821
2514
Il Rendimento Medio Contabile
Il rendimento medio contabile (RMC) è definito come:
il rapporto tra la redditività media incrementale prodotta nel
corso dei periodi presi in considerazione e l’ammontare
dell’investimento medio da sostenere.
RMC
reddito medio annuo
investimen to medio annuo
Si deve dunque dividere i profitti medi previsti dal progetto, al
netto degli ammortamenti e delle imposte, per il valore contabile
medio dell’investimento.
Questo rapporto viene confrontato con il rendimento medio
dell’impresa, con l’obiettivo di rendimento atteso, o con un
bechmark di riferimento (settore, peers).
Alcuni limiti del Rendimento Medio Contabile
1.
Non considera nè la distribuzione temporale dei flussi (se il reddito
viene prodotto il prossimo anno o il prossimo secolo) né il valore della
moneta nel tempo (rischio e inflazione);
2.
Non considera flussi di cassa, ma flussi di reddito;
3.
Non assume un valore univoco, perché risente dei principi contabili
adottati nella redazione del bilancio (ammortamento, principio di
competenza);
4.
Considera valori medi che, per definizione, sono approssimazioni.
Indice
Introduzione
I criteri tradizionali di valutazione dei progetti d’ investimento
I criteri finanziari di valutazione degli investimenti:
1.
Il valore attuale netto
2.
Il tasso interno di rendimento
3.
L’indice di rendimento attualizzato
I criteri finanziari
Caratteristiche comuni a tutti i criteri finanziari di analisi degli
investimenti sono:
1.
La considerazione dei flussi di cassa incrementali del progetto;
2.
L’impiego di un tasso di attualizzazione espressione del profilo di
rischio e rendimento del progetto.
1 - Quale flusso di cassa?
Flussi di cassa incrementali (with without principle)
al netto delle imposte;
al lordo della gestione finanziaria;
periodicità coerente con il piano di rimborso del debito e con
l’analisi economica di riferimento.
Principio di cassa, non di
competenza!
2 - Il tasso di attualizzazione - Il valore finanziario
del tempo
Due investimenti con flussi di cassa uguali in dimensione
assoluta, ma distribuzione temporale rovesciata, sono
indifferenti?
Figura A
Figura B
F
F
t
…..Preferite avere un milione domani o fra un anno?
t
2 - Il tasso di attualizzazione - Il valore finanziario del
tempo
F
k = costo del capitale
k
t
k
l’anticipo di un’entrata o il
ritardo di un’uscita
2 - Il tasso di attualizzazione - Il valore finanziario
del tempo
Anticipazione di un’entrata
Posticipazione di un’uscita
Costo
del capitale
Il valore attuale netto - VAN (o NPV o DCF o REA)
Il valore attuale netto esprime la ricchezza creata o
distrutta dal progetto, in unità monetarie;
Se il Van è positivo, significa che il progetto libera flussi di
cassa sufficienti a ripagare tutti i finanziatori. Ciò che rimane
è ricchezza aggiuntiva disponibile per l’impresa.
Il valore attuale netto (VAN, NPV, DCF, REA)
il VAN è la somma algebrica di TUTTI i flussi di cassa
attualizzati (positivi e negativi) generati dal progetto
considerato;
Rappresenta la ricchezza incrementale generata da un
progetto, espressa come se fosse immediatamente disponibile;
Quindi: se il VAN è positivo c’è creazione di valore !
Il valore attuale netto (VAN, NPV, DCF, REA)
In formule:
VAN
F
F
F
F1
F
F
2 2 3 3 4 4 5 5 6 6 F0
(1 k ) (1 k ) (1 k ) (1 k ) (1 k ) (1 k )
Più in generale:
n
Ft
VAN
F0
t
t 1 (1 k )
Dove:
F: flusso di cassa
k: tasso di sconto
n
Ossia:
Ft
t
t 0 (1 k )
VAN
Il valore attuale netto (VAN, NPV, DCF, REA)
Esempio:
Viene effettuato un investimento di 100 convinti che questo
comporterà flussi di cassa di entrata per 7 anni secondo il seguente
andamento:
Anni
1
2
3
4
5
6
7
Flussi previsti
15
17
19
21
24
24
25
La regola è: si devono accettare gli investimenti il cui tasso interno
di rendimento (IRR) è superiore al costo-opportunità del capitale
Il valore attuale netto (VAN, NPV, DCF, REA)
Esempio:
I flussi di cassa devono essere attualizzati per renderli confrontabili;
Per fare l’investimento si è rinunciato ad un investimento di pari
rischio che offriva l’8% di interesse…..
Anni
1
2
3
4
5
6
7
Flussi previsti
Flussi attualizzati
15
13,9
17
14,6
19
15,1
21
15,4
24
16,3
24
15,1
25
14,6
La regola è: si devono accettare gli investimenti il cui tasso interno
di rendimento (IRR) è superiore al costo-opportunità del capitale
Il valore attuale netto (VAN, NPV, DCF, REA)
Esempio:
Si ha quindi modo di ricavare i flussi di cassa complessivi del
progetto ………
Anni
1
2
3
4
5
6
7
Flussi previsti
15
17
19
21
24
24
25
Flussi attualizzati
Flussi complessivi
13,9
14,6
15,1
15,4
16,3
15,1
14,6
-100,0
13,9
14,6
15,1
15,4
16,3
15,1
14,6
Il valore attuale netto (VAN, NPV, DCF, REA)
Esempio:
…….il cui VAN è positivo e pari a 5. Il progetto “rende” più di
quanto vorrei (…. mi “accontentavo” dell’8% !)
Anni
1
2
3
4
5
6
7
Flussi previsti
15
17
19
21
24
24
25
Flussi attualizzati
Flussi complessivi
13,9
14,6
15,1
15,4
16,3
15,1
14,6
-100,0
13,9
14,6
15,1
15,4
16,3
15,1
14,6
VAN
5,0
Il tasso interno di rendimento – TIR (o IRR o TIM)
Il tasso interno di rendimento (IRR) è quel particolare tasso di
attualizzazione che rende identici i valori dei flussi positivi e
negativi di un progetto (quello che rende il VAN uguale a zero);
Quindi:
L’IRR rappresenta il costo massimo della raccolta che un
progetto può sopportare, affinché permanga la sua convenienza
economica;
L’IRR rappresenta il rendimento lordo di un progetto di
investimento. Il rendimento è lordo poiché non si considera il
costo delle risorse utilizzate.
La regola è: si devono accettare gli investimenti il cui tasso interno
di rendimento (IRR) è superiore al costo-opportunità del capitale
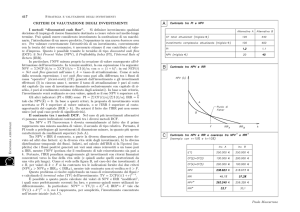
Il tasso interno di rendimento (IRR, TIM, TIR)
Graficamente:
REA
VAN
2514
k*
864
20%
10%
IRR
Creazione di valore
Distruzione di valore
k
Il tasso interno di rendimento (IRR, TIM, TIR)
Il concetto di rendimento è intuitivo:
Tasso di rendimento
Sfortunatamente, se i flussi sono più di uno, il calcolo non è
immediato, ma si deve procedere …per tentativi!
VAN F0
Ft
F1
F2
...
0
1 IRR 1 IRR 2
1 IRR t
n
Ossia:
Entrata
1
Investimen to
Ft
(1 IRR )
t 1
t
F0 0
In MS Excel™, la formula da usare è “=TIR.COST(valori)”, altrimenti si
può procedere impostando una proporzione (si ipotizza che in un
intervallo sufficientemente breve la curva sia assimilabile ad una retta)
Limiti del TIR (o IRR o TIM)
Non dice quale sia il valore creato dall’investimento, quindi non
aiuta a decidere fra 2 investimenti alternativi (a parità di IRR o
con IRR diversi);
L’ipotesi implicita è che i flussi liberati dal progetto vengono
reinvestiti al IRR;
Non sempre fornisce un valore unico.
L’Indice di redditività (IRA, costo/beneficio)
L’indice di rendimento attualizzato (IRA) è il rapporto tra il
valore attuale dei flussi positivi generati dall’investimento e il
flusso iniziale F0 (o il valore attuale delle uscite necessarie alla
realizzazione del progetto, qualora le stesse siano più d’una);
Esprime l’efficienza di un progetto: se investo 1 Euro, quanti
Euro vengono liberati?
In formula:
n
IRA
F
t 1
t
(1 k ) 1
F0
IRA = 12.514 /10.000 =
1,2514
L’Indice di redditività (IRA, costo/beneficio)
L’indicazione principale è : “accettare progetti con IRA > 1”
ma
Non dice quale progetto crea più ricchezza;
può essere utile per ordinare i progetti per efficienza decrescente,
scegliendo i progetti che massimizzano il VAN complessivo.
Esempio
Fo
F1
VAN
IRA
A
50
75
25
1,50
INVESTIMENTI
B
C
40
60
55
87
15
27
1,38
1,45
D
20
35
15
1,75
Se il vincolo è 60, occorre valutare se è possibile
sommare gli investimenti B+D o effettuare 3 volte D