La luce

La luce
La luce è energia radiante elettromagnetica che
l’occhio umano riesce a percepire. E’
caratterizzata dalla lunghezza dell’onda λ e dalla
sua frequenza ν, legate dalla relazione:
c=νλ
“c” la velocità della luce nel vuoto (circa
300.000 km/s).
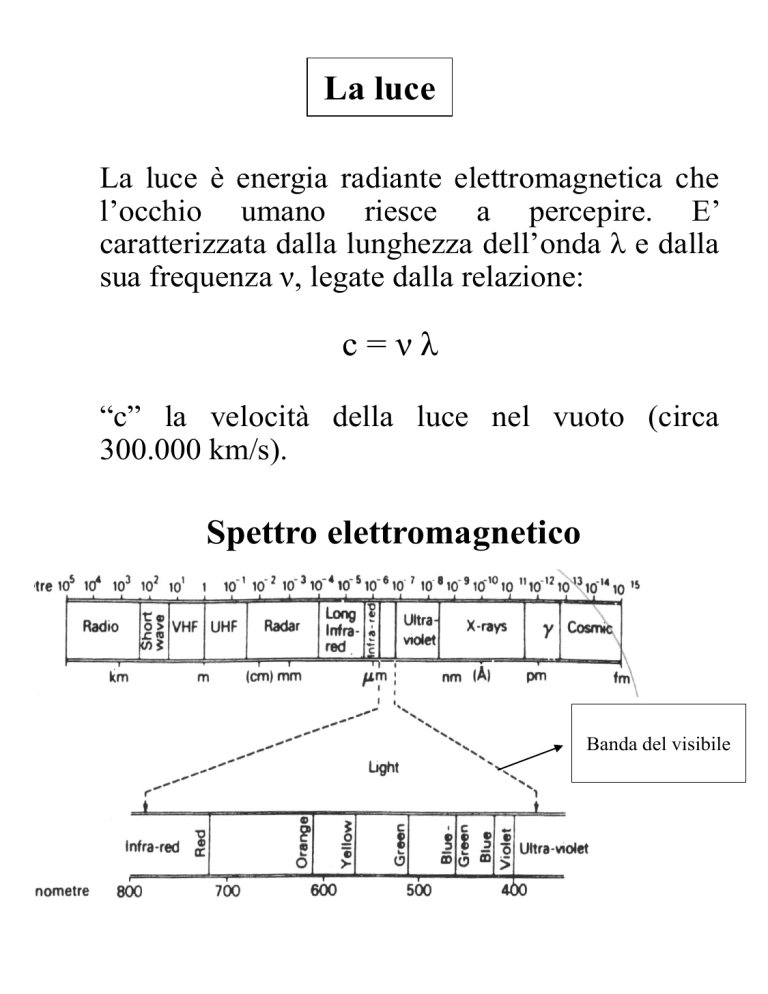
Spettro elettromagnetico
Banda del visibile
La luce
Un raggio luminoso che incide una superficie può essere
RIFLESSO, ASSORBITO o TRASMESSO.
-
Coefficiente di riflessione
(): [En. Riflessa /En. Incidente]
Coefficiente di assorbimento (): [En.assorbita/ En. Incidente]
Coefficiente di trasmissione (): [En.trasmessa/En. Incidente]
Deve risultare che:
 +  +  =1
Riflessione speculare: Raggi riflessi
mantenuti paralleli.
Angolo incidenza=Angolo riflessione
Riflessione diffusa: la luce riflessa si
distribuisce in intensità e direzione
descrivendo una superficie sferica tangente
alla superficie (superfici lambertiane)
Effetto sovrapposto: la riflessione dei raggi
avviene in tutte le direzioni ma si concentra
intorno alle direzioni vicine a quella della
riflessione speculare
La luce
Corpo trasparente se trasmette la luce.
Corpo opaco se blocca il passaggio della luce.
In realtà, nessun materiale è completamente trasparente o
completamente opaco.
Rifrazione
Passaggio della luce da un da un mezzo ad un altro con
densità ottica diversa (p.e. dall’aria all’acqua o vice-versa)
La rifrazione comporta un cambiamento
di direzione del raggio incidente.
Il fenomeno della rifrazione, dipende dal cambiamento
di velocità di propagazione della luce nei diversi mezzi
e, in una certa misura, dalla lunghezza d’onda
Indice di Rifrazione: rapporto fra la velocità della luce
nel vuoto (2,998x108 m/s) e quella in un altro mezzo
Rifrazione
i
r
Si osserva che:
- il raggio incidente, il raggio rifratto e la interfaccia
fra i due mezzi sono contenuti nello stesso piano
- il rapporto fra il seno dell’angolo rifratto (αr) e il
seno dell’angolo incidente (αi) è uguale al rapporto
degli indici di rifrazione del mezzo di provenienza
(n1) e del mezzo di arrivo (n2) (il che equivale
all’inverso del rapporto fra le velocità di
propagazione).
Legge di Snell
sen  r n1 v2


sen  i n2 v1
Rifrazione
- L’indice di rifrazione è un rapporto di velocità e
quindi è un numero adimensionale.
- La rifrazione dipende anche da : un raggio
luminoso di lunghezza d'onda minore, subisce una
rifrazione maggiore.
- L’indice di rifrazione assoluto di un mezzo è il
rapporto della velocità della luce nel mezzo, rispetto
alla velocità della luce nel vuoto, al quale si
attribuisce indice di rifrazione n = 1.
Indice di rifrazione dell’aria rispetto all’acqua = 1.33.
n1 sen  r

1
n2 sen  i
1) Aria
i
r
2) Acqua
Il primo mezzo è più
rifrangente del secondo
angolo di incidenza > angolo di rifrazione
Doppia- Rifrazione
1) Aria
i
r
i
2) Acqua
3) Aria
Una radiazione monocromatica che attraversa un
mezzo trasparente di spessore finito (ad esempio
una lastra di vetro) viene sottoposta a due rifrazioni
consecutive.
Se le due superficie di interfaccia aria-vetro e
vetro-aria sono fra loro parallele, si ottiene una
semplice traslazione dei raggi che manterranno
comunque la direzione originale
I colori
• A ciascuna lunghezza d’onda della radiazione
luminosa compresa nel cosiddetto intervallo del
visibile corrisponde una diversa sensazione visiva,
la cui qualità è associata al concetto di colore.
• La luce con uno spettro elettromagnetico di
dimensioni infinitesime si dice monocromatica.
• La luce bianca del sole è una miscela di tutte le
radiazioni con lunghezze d’onda comprese nel
visibile e di radiazioni che si trovano all’esterno di
tale intervallo
Una sorgente luminosa viene caratterizzare dal
punto di vista cromatico attribuendo alla sua
luce una cosiddetta temperatura di colore
correlata.
Si definisce “temperatura di colore” la
temperatura (espressa in Kelvin) di un corpo
nero che emette luce dello stesso colore
I colori
Il sole ha uno spettro di emissione molto simile a quello
di un corpo nero la cui temperatura è di 5780 K,
Dalla legge di Wien segue che maggiore è la
temperatura del corpo nero, minore è la temperatura
a cui si ha il picco di emissione
Questo spiega perché, nell’accezione comune, una
luce con prevalenza di rosso viene definita calda
anche se la temperatura di colore ad essa associata
risulta relativamente bassa. Al contrario una luce
violetta, definita fredda ha una temperatura elevata.
I colori: Ruota di Munsell
Questa classificazione definisce tre attributi dei colori:
· Tinta (Hue Scale): è la sensazione percepita che dà
il nome al colore: giallo, rosso, blu; sono previsti
colori intermedi e una suddivisione numerica degli
stessi
· Valore di brillantezza (Value Scale): è una misura
soggettiva dell’intensità percepita dell’oggetto
riflettente, misurata su una scala che va da 0 (nero
assoluto) a 10 (bianco perfetto);
· Croma o saturazione (Chrome) : è la pienezza o
l’intensità del colore; per ogni colore sono definite
delle classi, in numero variabile, di saturazione; il
numero minimo di classi (10) è associato al colore
blu, il numero massimo (18) al rosso.
I colori: Ruota di Munsell
- Sull’asse di tale ruota è riportata la scala del
valore: dal basso verso l’alto si passa dal nero al
bianco.
- Su 10 diversi raggi della ruota sono individuate la
10 tinte fondamentali: rosso, giallo, verde, blu,
viola, giallo-rosso, verde-giallo, viola-blu e rossoviola. Ciascuna delle tinte fondamentali è a sua
volta suddivisa in 10 sottotinte.
- Sul raggio di ciascuna tinta è riportata la scala del
croma: in corrispondenza dell’origine del raggio il
colore ha la saturazione minima, man mano che ci si
allontana il valore di saturazione cresce.
Ciascun colore viene individuato attraverso una sigla:
Tinta-Brillantezza/Croma
ESEMPIO: 5P – 5/8 rappresenta il viola di tinta 5,
Brillantezza 5 e Croma 8.
Ruota di Munsell
Sistema CIE (Commission International d’Eclarage)
Qualunque colore può essere ottenuto attraverso la
miscelazione di tre colori primari opportunamente scelti.
SISTEMA (RGB): X= Rosso
Y= Verde
Z= Blu
X+Y+Z=1
E’ sufficiente conoscere due coordinate per calcolare
agevolmente la terza, quindi, è sufficiente una
rappresentazione bidimensionale in luogo di una
tridimensionale (CARTA CROMATICA).
- I colori spettrali sono rappresentati sul perimetro della
curva, a forma di parabola.
- I colori non spettrali (viola e magenta) si trovano sul
segmento di retta che congiunge i due estremi liberi della
parabola.
- La zona centrale del diagramma rappresenta il bianco.
- Tutti i colori reali si trovano all’interno della curva.
- Tutti i colori compresi all’interno di essi possono essere
ottenuti miscelando quantità positive dei tre colori
primari
Sistema CIE (Commission International d’Eclarage)
Grandezze Fotometriche
Flusso Luminoso “F”
Quantità di energia luminosa (percepita dall’occhio
umano) emessa nell’unità di tempo da una sorgente entro
un angolo solido ω . Si misura in lumen (lm).
La tabella seguente riporta alcuni valori di flusso
luminoso emesso da sorgenti di comune impiego:
• Lampada ad incandescenza da 100 W
975 lm
• Lampada fluorescente da 38 W
2800 lm
• Lampada a vapori di mercurio da 400 W 20.000 lm
Intensità Luminosa “I”
Rapporto fra il flusso luminoso dF emesso da una
sorgente in una data direzione e l’angolo solido
infinitesimo dw di apertura del cono che ha per asse la
linea rappresentativa della direzione
dF l
I
[cd ]
dw
Grandezze Fotometriche
Intensità Luminosa “I”
Unità di misura è la Candela [cd]
Una sorgente puntiforme che emette uniformemente
in tutte le direzioni con l’intensità di 1 cd, racchiusa in
una sfera di raggio unitario, il flusso luminoso totale
risulterà pari a:
1 cd x 4 π = 12,56 cd x ster = 12,56 lumen
Grandezze Fotometriche
Intensità Luminosa “I”
Se la sorgente emette un flusso luminoso non uniforme in
tutte le direzioni, anche l’intensità luminosa varierà con
la direzione.
“Solido fotometrico”: rappresentazione polare delle
mappe tridimensionali delle intensità luminose.
Noto il solido fotometrico è possibile risalire al valore di
intensità luminosa in tutte le direzioni.
Se la sorgente presenta delle simmetrie intorno ad uno o
più assi, è possibile rappresentare il solido attraverso un
numero limitato di sezioni piane (curve fotometriche).
Grandezze Fotometriche
Illuminamento “E”
Rapporto fra il flusso luminoso misurato in lumen e
la superficie misurata in m2 .
Unità di misura è il Lux
dF l
E
dA
Nel caso di flusso lumino uniforme risulta:
Fl
E
A
[lux ]
[lux ]
Grandezze Fotometriche
Illuminamento “E”
L’illuminamento è una grandezza additiva.
Se “n” sorgenti generano ciascuna un
illuminamento Ei su un medesimo piano di lavoro,
l’illuminamento risultante sarà dato dalla somma
dei singoli illuminamenti:
Etot = Si Ei
L’illuminamento di una superficie si riduce
proporzionalmente al quadrato della distanza
dalla sorgente.
La relazione che lega l’illuminamento alla intensità
luminosa monodirezionale di una sorgente è la
seguente :
dF l Idw
I dA I
E


 2 [lux ]
2
dA
dA dA r
r
Grandezze Fotometriche
Illuminamento “E”
L’illuminamento su una superficie è maggiore
quando la direzione della luce è normale alla
superficie stessa.
In tutti gli altri casi la densità di flusso si riduce
poiché l’area della superficie su cui la luce si
distribuisce è maggiore
La superficie A2 è pari all’area proiettata sulla
normale diviso il coseno dell’angolo b
A1
I
I cos b
A2 
E


E

[lux ]
1
2
2
2
cos b
r
r
Grandezze Fotometriche
Luminanza “L”
La luminanza in un punto di una superficie in
una certa direzione, è il rapporto fra l’intensità
luminosa “I” emessa in quella direzione e l’area
della superficie emittente apparente.
Unità di misura è [cd/m2]
La superficie a cui fare riferimento per il calcolo
della luminanza è quella realmente vista
dall’osservatore.
Occorre calcolare la superficie apparente proiettando
l’area reale su un piano perpendicolare alla retta
direttrice osservatore- oggetto.
Grandezze Fotometriche
Luminanza “L”
dI
dL 
cos 
dA
 cd 
 m 2 
Se la superficie diffonde uniformemente in tutte le
direzioni (superficie lambertiana ) allora la sua
luminanza sarà:
L
I

 cd 
 m 2 
Radianza “R”
Rapporto fra il flusso luminoso e l’area della
superficie emittente.
dF l
R
dA
 lm 
 m 2 
L’unità di misura della radianza è lm/m2
(dimensionalmente omogenea all’illuminamento).
Il flusso luminoso che viene considerato per
misurare la radianza può però essere generato o da
una riflessione (e quindi R = ρE ) o da una
trasmissione (R = τE)
Grandezze Fotometriche
L’effetto luminoso e visivo della radiazione
emessa da una sorgente dipende dalla sua
lunghezza d’onda.
L’occhio umano ha una sensibilità che non è
costante in tutto l’intervallo del visibile dello
spettro elettromagnetico: gli impulsi generati sulla
retina dalle stesse quantità di energia a diverse
lunghezze d’onda non sono uguali
Si introducono dei fattori di ponderazione (o
fattori di visibilità v() )per ciascuna lunghezza
d’onda
Si effettua la conversione energia-sensazione
luminosa.
Grandezze Fotometriche
I fattori di ponderazione v() riportati in un
diagramma sulle cui ascisse ci sono le lunghezze
d’onda, descrivono una curva a campana
(CIE standard luminous efficacy curve)
Il picco è posto in corrispondenza dei 550 nm nel
caso di visione fotopica e dei 507 nm nel caso di
visone scotopica (notturna).
Grandezze Fotometriche
In corrispondenza della lunghezza d’onda in cui si
ha il picco di sensazione visiva, una radiazione di
1 W genera un flusso luminoso di 680 lm.
Il flusso luminoso equivalente Fl corrispondente
ad una radiazione F emessa in un intervallo
infinitesimo d dello spettro è:
F l = 680 F () v() d
Nel caso di una radiazione estesa ad un
intervallo finito dello spettro
2
Fl = 680 1 F () v() d
Grandezze Fotometriche
Efficienza Luminosa “ “
Rapporto fra il flusso luminoso emesso (Fl)
dalla sorgente nel campo del visibile e la
potenza necessaria a generare la radiazione
di onde elettromagnetiche (W).
Fl

W
la misura dell’efficienza luminosa è lm/W
Coefficiente di visibilità “k”
Rappresenta il rapporto fra il flusso
luminoso e il flusso radiante emesso dalla
sorgente nel campo del visibile
Fl
k
F vis
Fvis è una grandezza energetica (W).
Grandezze Fotometriche
Efficienza ottica della sorgente “o“
Considerando solo gli aspetti energetici della
sorgente (escludendo l’uso dei fattori di visibilità
relativa) e misurando tutti i flussi radiati (F) in
watt
F vis
o 
F
Efficienza radiante “r“
Rapporto fra la potenza emessa e quella
necessaria a generare la radiazione di onde
elettromagnetiche
F
r 
W
Il prodotto di r o k
è uguale all’efficienza
luminosa della sorgente:
Fl
F F vis F l
l   r 0 k 

W F F vis W
Grandezze Fotometriche
Resa cromatica “Ra”
Attitudine di una sorgente luminosa a rendere i colori
degli oggetti illuminati senza alterazioni
Si esprime mediante un indice Ra che varia fra 0 e 100
Quanto maggiore è Ra di una lampada tanto più essa
permette di apprezzare realisticamente i colori
Gruppo di resa di colore
Resa cromatica, Ra
1A
91÷100
1B
81÷90
2
61÷80
3
41÷60
4
21÷40
Grandezze Fotometriche
Tonalità di colore

Le normative (UNI e CIE) definiscono tre gruppi di
sorgenti in qualità della temperatura di colore
associata alla radiazione emessa:
- gruppo W (white): luce bianco-calda, temperatura di
colore < 3300 K;
- gruppo I (intermediate): luce bianco-neutra,
temperatura di colore tra 3300 e 5300 K;
- gruppo C (cold): luce bianco-fredda, temperatura di
colore > 5300 K.