Giuseppe Rodonò
Ruggero Volpes
Appunti di Fisica tecnica
Fotometria
Università degli studi di Palermo
Dipartimento di Energetica
Palermo, 1999
I
INDICE
SIMBOLI
pagina
II
1. LA FUNZIONE VISIVA
1.1. Le onde elettromagnetiche
1.2. L'occhio
1.3. Stimolo fisico e percezione
1.4. Visione fotopica e visione
scotopica
1.5. Curve normali di visibilità
1
1
2
4
2. FOTOMETRIA
2.1. Generalità
2.2. Grandezze fotometriche
2.2.1. Flusso luminoso
2.2.2. Intensità luminosa
2.2.3. Radianza
2.2.4. Luminanza
2.2.5. Illuminamento
2.3. Sorgenti secondarie
2.4. Misura delle grandezze fotometriche
2.4.1. Illuminamento
2.4.2. Intensità luminosa
2.4.3. Luminanza
2.4.4. Flusso luminoso
2.5. Temperatura di colore
9
9
9
9
10
13
13
14
16
3. SORGENTI DI LUCE
3.1. Generalità
3.2. Lampade a incandescenza
3.3. Lampade a scarica
3.3.1. La scarica nei gas
25
25
26
29
29
6
7
17
17
18
20
21
24
3.3.2. Lampade a vapori di mercurio
3.3.3. Lampade a vapori di sodio
3.3.4. Lampade allo xeno
3.3.5. Tubi ad alta tensione
3.4. Lampade fluorescenti
3.4.1. La fluorescenza
3.4.2. Lampade fluorescenti
tubolari
3.4.3. Lampade fluorescenti a
bulbo
3.4.3. Lampade a luce miscelata
3.5. Lampade a combustione
4. ILLUMINAZIONE DEGLI
AMBIENTI CHIUSI
4.1. Requisiti dell'impianto
d'illuminazione
4.1.1. Illuminamento
4.1.2. Illuminazione localizzata
4.1.3. Abbagliamento
4.1.3. Colore della luce
4.2. Illuminamento prodotto da
una sorgente puntiforme
4.3. Illuminamento prodotto da
una sorgente estesa
4.4. Metodo del flusso totale
33
34
35
35
35
35
36
36
37
37
39
39
39
41
41
42
42
44
46
BIBLIOGRAFIA
49
INDICE ANALITICO
50
II
SIMBOLI
A
c
C
d
EV
i
area
velocità della luce
contrasto di luminanza
durata delle lampade
illuminamento
corrente elettrica; indice del locale
I intensità (energetica) dell'irradiamento
IV intensità luminosa
KM fattore costante nella definizione
del flusso luminoso
LV luminanza
MV radianza o emittanza luminosa
n indice di rifrazione
r
coefficiente di riflessione diffusa
(albedo); distanza; raggio
S area
T temperatura termodinamica
u fattore di utilizzazione
V coefficiente di visibilità relativa;
tensione elettrica
W potenza
α angolo
λ lunghezza d'onda
ν frequenza
τ tempo
ΦV flusso luminoso
ϕ angolo
Ω angolo solido
1
1. LA FUNZIONE VISIVA
1.1. Le onde elettromagnetiche
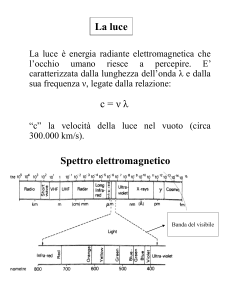
L'occhio umano è un rivelatore di una classe di onde elettromagnetiche, cioè di
quelle che hanno una lunghezza d'onda nel vuoto compresa tra 380 nm e 780 nm.
Tali radiazioni sono dette radiazioni luminose o semplicemente luce; le altre radiazioni elettromagnetiche non sono percepite dal nostro apparato visivo.
Caratteristica comune di tutte le radiazioni elettromagnetiche è la velocità di propagazione nel vuoto, comunemente detta velocità della luce e indicata col simbolo c.
Questa velocità è:
c = 2 ,9979 × 108 m/s .
(1)
La velocità cn di propagazione in un mezzo diverso dal vuoto è:
c
cn =
(2)
n
dove n ≤ 1 è l'indice di rifrazione del mezzo.
Prendendo in considerazione l'aspetto oscillatorio delle radiazioni elettromagnetiche, caratterizziamo una radiazione per mezzo della sua frequenza ν, che è il numero di oscillazioni del campo elettromagnetico che hanno luogo nell'unità di tempo in un dato posto. Misuriamo la frequenza in hertz (1 Hz = 1 s-1). Il rapporto tra
la velocità della luce e la frequenza della radiazione dà la lunghezza d'onda λ. Nel
vuoto è:
c
λ= .
(3)
ν
In un mezzo diverso dal vuoto abbiamo dalla (2):
c
c
λ= n =
.
(4)
ν nν
Osserviamo che il valore di ν dipende dalla natura del mezzo, dal suo stato termodinamico e dalla frequenza della radiazione. Nel passaggio di una radiazione da un
dato mezzo a un altro, che abbia un diverso indice di rifrazione n, mentre la frequenza n rimane invariata, la lunghezza d'onda cambia secondo la (4). Nella massima parte dei casi che si considerano nella tecnica della illuminazione il mezzo è
l'aria, il cui indice di rifrazione è poco diverso da 1; una radiazione perciò può essere descritta per mezzo della sua lunghezza d'onda, per la quale si intende la lunghezza d'onda nel vuoto, come si ricava dalla (4) ponendo n = 1.
Al variare della frequenza ν mutano gli effetti prodotti dalla radiazione elettromagnetica sui materiali, sui tessuti biologici e sugli organi di senso, con i quali essa
viene a interagire; perciò si usa denominare la radiazione con nomi diversi a seconda della frequenza, come mostrato nella tabella.
APPUNTI DI FISICA TECNICA: FOTOMETRIA
2
La radiazione visibile, in quanto capace di stimolare gli organi della vista, è detta luce. Non sono perciò appropriate espressioni come luce ultravioletta, luce di Wood, etc.
Una radiazione elettromagnetica, incontrando un corpo, generalmente ne viene in
parte rinviata, mentre per il resto penetra in esso; quest'ultima parte può attraversare il corpo riemergendone dopo averne percorso lo spessore o esserne, anche in parte, assorbita. Si parla allora, a seconda del caso, di corpi riflettenti (in
modo speculare o diffuso), trasparenti, opachi. Si fa anche una distinzione tra corpi propriamente trasparenti (quelli che trasmettono la radiazione senza dispersione,
Classificazione delle onde elettromagnetiche
denominazione
Raggi cosmici
Raggi γ
Raggi X
Raggi UV
Radiazione visibile
Radiazione infrarossa
Onde radio:
microonde (radar, TV)
metriche (VHF): TV
decametriche (corte)
ettometriche (medie)
kilometriche (lunghe)
miriametriche (VLF): radioaiuti alla navigazione
Onde a frequenza acustica
(telefonia)
lunghezza d'onda nel
vuoto
1 fm 10 fm
1 fm 10 pm
1 pm 10 nm
10 nm 380 nm
780 nm 380 nm
780 nm 1 mm
30000 EHz 300000 EHz
30 EHz 300 000 PHz
30 PHz 300 EHz
790 THz 30 PHz
370 THz 790 THz
300 GHz 300 THz
1 mm 1 m
1 m 10 m
10 m 100 m
100 m 1 km
1 km 10 km
300 MHz 300 GHz
30 MHz 300 MHz
3 MHz 30 MHz
300 kHz 3 MHz
30 kHz 300 kHz
10 km 100 km
3 kHz 30 kHz
100 km 10 000 km
30 Hz 3 kHz
frequenza
cosicché si può guardare attraverso di essi) e traslucidi (quelli che trasmettono sì
la radiazione, ma disperdendola, sicché attraverso di essi si vede filtrare la luce ma
non si vedono le immagini).
Può accadere che l'energia assorbita in un corpo dia luogo semplicemente allo sviluppo di una pari quantità di calore, ma può anche avvenire che la materia, dopo
avere acquistato l'energia, successivamente la rilasci ancora sotto forma di energia
elettromagnetica di diversa lunghezza d'onda (fluorescenza). In altri casi l'energia
acquistata dal corpo vi rimane sotto forma di energia chimica o di ionizzazione,
etc. Di questi fenomeni si approfitta per la realizzazione di sorgenti artificiali di luce, di cui si parlerà al cap. 4.
1.2. L'occhio
Nell'apparato della visione dell'uomo l'occhio è l'elemento ricevitore. Esso costituisce un sistema ottico paragonabile a un gruppo di lenti. Vi si distinguono:
- la camera anteriore di forma lenticolare, piena di umore acqueo; essa è delimitata
verso l'esterno da un rivestimento trasparente (còrnea) e verso l'interno dal cristalli-
1. LA FUNZIONE VISIVA
3
no, sorta di lente biconvessa, che alcuni muscoli connessi alla sua periferia possono
deformare, così da modificarne la distanza f ocale;
- l'umore vìtreo, corpo gelat inoso che riempie la rimanente cavità del bulbo oculare, anch'esso funzionante da lente;
- tra la camera anteriore e il cristallino è posta l'ì ride, una membrana opaca che
porta al centro un'apertura di diametro variabile (pupilla), che consente il passaggio
della luce.
Le deformazioni del cristallino modificano le caratteristiche di tutto il sistema ottico;
la radiazione proveniente dall'esterno viene sempre rifratta
in modo tale che sul fondo del
globo oculare si crea un'immagine reale nitida (a fuoco)
di ciò che si trova all'esterno.
Sezione schematica dell'occhio.
L'organo ricevitore vero e
proprio è la rètina. Questa è una sottile membrana che ricopre tutto il fondo oculare. Essa è ricchissima di terminazioni nervose sensibili alle radiazioni elettromagnetiche aventi lunghezza d'onda compresa nella banda della radiazione visibile. Le
risposte nervose agli stimoli che nascono nelle cellule fotosensibili della retina vengono trasmesse al cervello attraverso il nervo ottico, che costituisce la continuazione delle cellule nervose della retina verso l'esterno del globo oculare.
L'intensità della risposta dell'occhio alla radiazione stimolatrice dipende in generale
dalla potenza della radiazione stessa e non dalla durata. Se però tale durata è inferiore a circa 0,1 s, allora la sensazione percepita dipende dall'energia della radiazione.
Oltre a queste caratteristiche morfologiche dell'occhio, alcune caratteristiche funzionali sono degne di
nota. Tra queste, si è già accennato alla capacità del cristallino di adeguarsi alla distanza dell'oggetto
che si vuole guardare, così che l'im magine reale (1) di questo venga a formarsi nitida sulla superficie
retinica (accomodazione). A riposo la forma del cristallino è tale che sulla retina si forma nitida l'immagine di ciò che è posto a grande distanza (punto all'infinito). Con l'azione dei muscoli interni all'occhio che contornano il cristallino questo può deformarsi riducendo la sua distanza focale; ciò permette
di mettere a fuoco sulla retina l'immagine degli oggetti distanti fino a soli 15 cm ( punto prossimo).
Un'altra capacità di regolazione riguarda l'intensità dello stimolo luminoso, che può essere variata entro certi limiti dal dispositivo a diaframma circolare, a cui si è già accennato (ìride ). Questo è in grado
1
) Si dice immagine reale l'immagine prodotta da un qualunque sistema ottico su uno schermo e visibile con l'osservazione da una qualunque posizione (esempio: l'immagine proiettata sullo schermo cinematografico). Si dice immagine virtuale l'immagine, anch'essa prodotta da un sistema ottico, che
non è data da una reale distribuzione spaziale di superficie emittente, pur dandone la stessa sensazione. È un'immagine virtuale quella visibile attraverso l'oculare di un telescopio o una lente da occhiali. In generale si può osservare un'immagine virtuale solo ponendo l'occhio in una data posizione,
da dove il sistema ottico la rende visibile.
4
APPUNTI DI FISICA TECNICA: FOTOMETRIA
di allargare o restringere il diametro della pupilla a seconda della densità superficiale di potenza (più
correttamente: dell'illuminamento; v. § 2.2.5) incidente sulla pupilla. Il funzionamento di quest'organo
è involontario e consente di variare il diametro della pupilla nell'intervallo da 8 a 2 mm; corrispondentemente l'area della pupilla varia tra un massimo e un minimo che stanno nel rapporto di circa 16:1;
nello stesso rapporto varia il flusso luminoso raccolto dall'occhio e incidente sulla rètina. Pare che
questa funzione dell'iride non sia molto importante, poiché la retina ha un campo dinamico di funzionamento molto esteso, con un rapporto tra il massimo e il minimo di luminanza osservabile di ben
1012 (= 120 dB).
Un'importante funzione dell'iride è quella di restringersi nell'osservazione degli oggetti vicini, così da
migliorare la nitidezza dell'immagine e collaborare col cristallino alla funzione dell'accomodazione.
Infatti in qualunque sistema ottico, e così pure nell'occhio, al diminuire del l'apertura della lente diminuiscono le aberrazioni geometriche e aumenta la profondità di campo, cioè l'intervallo delle distanze
degli oggetti, le cui immagini sono contemporaneamente riprodotte con nitidezza dal sistema ottico.
Si definisce l'acuità (ossia acutezza) visiva, che è la capacità di riconoscere con l'osservazione come
distinti due punti molto vicini. Tale capacità è variabile a seconda dell'osservatore e delle condizioni di
osservazione; in generale si suole identificare l'acuità visiva normale come la capacità di discernere
due punti che siano estremi di un arco visto sotto l'angolo di 1', ciò che corrisponde, per esempio, a
due punti distanti tra loro 1 mm e osservati dalla distanza di 3,4 m.
È importante il fenomeno della persistenza delle immagini sulla rètina anche dopo che sia cessato lo
stimolo visivo. Il fenomeno si verifica perché il funzionamento delle cellule fotosensibili si fonda su
alcune modificazioni fisiche e chimiche che hanno luogo in queste cellule quando esse sono colpite
dalla luce; al variare del flusso luminoso incidente sui fotorecettori le corrispondenti modificazioni impiegano un certo tempo per compiersi. Ciò determina un certo ritardo nella variazione della percezione, quindi anche la persistenza dell'immagine durante un certo tempo dopo che lo stimolo luminoso è
cessato.
La persistenza delle immagini nel tempo è tanto maggiore quanto più intenso lo stimolo. In condizioni
normali la durata della persistenza va da 0,1 a 0,05 s, ma in seguito all'osservazione di sorgenti luminose di grande luminanza si può avere una persistenza anche di diversi secondi.
Varii altri fenomeni sono connessi con lo svolgimento della funzione visiva nelle diverse situazioni.
Alcuni di questi dipendono dalle proprietà ottiche dell'occhio o dalle caratteristiche dei muscoli che ne
permettono il movimento; altri fenomeni sono dipendenti dai processi psichici conseguenti alla ricezione dell'immagine sulla retina e sono perciò di più difficile interpretazione e schematizzazione. Su
alcuni di questi fenomeni si tornerà in seguito nella discussione sui requisiti degli impianti di illuminazione.
1.3. Stimolo fisico e percezione
La sensazione visiva prodotta dall'osservazione di una sorgente luminosa o di una
superficie illuminata da un'altra sorgente è distinta da tre caratteri:
- la brillanza, in base alla quale un corpo sembra emettere più o meno luce per unità
di superficie;
- la tinta o tono di colore, che è quell'attributo della percezione visiva che ci fa distinguere il giallo dal verde, dal rosso etc.;
- la saturazione, che indica la purezza cromatica della luce. Si considerano con saturazione pari a uno i colori associati alle radiazioni monocromatiche, cioè i colori
ottenibili dalla scomposizione della radiazione solare con uno spettroscopio; ha
saturazione uguale a zero la luce bianca priva di una particolare tinta. Un colore
1. LA FUNZIONE VISIVA
5
rosa è in una condizione intermedia e può essere considerato come un rosso a bassa saturazione.
Questi tre caratteri sono proprii della sensazione; essi sono perciò delle grandezze
Corrispondenza tra i caratteri dello stimolo e i caratteri della percezione
Caratteri dello stimolo
Caratteri della percezione
lunghezza d'onda domipurezza colorimetrica
nante
tinta
saturazione
luminanza
brillanza
soggettive, ossia di natura psicologica e non fisica, anche se sono determinati dalle
grandezze fisiche proprie della radiazione. Chiamiamo stimolo la radiazione che è
causa della sensazione visiva; quest'ultima è la percezione. Il problema centrale
della Fotometria è la corrispondenza tra i caratteri fisici dello stimolo (grandezze di
natura oggettiva) e i caratteri della risposta fisiopsicologica (percezione) elaborata
dall'individuo che riceve lo stimolo.
La brillanza di una superficie è strettamente legata alla luminanza, grandezza definita al § 2.2.4.
Alla tinta corrisponde, come grandezza fisica, la lunghezza d'onda dominante: questa è la lunghezza d'onda di uno stimolo monocromatico che, addizionato in opportuna proporzione a uno stimolo acromatico (bianco), permette di riprodurre lo stimolo di colore considerato. Si precisa che è detta stimolo acromatico una radiazione capace di provocare una percezione di colore con saturazione nulla.
Con riferimento alla stessa definizione e nelle stesse condizioni, si chiama purezza
colorimetrica dello stimolo di colore il rapporto tra il flusso ΦV della radiazione
monocromatica e il flusso luminoso totale (radiazione monocromatica + radiazione
acromatica). Anche il flusso luminoso è una grandezza fisica, di cui al § 2.2.1 sarà
data la definizione. La purezza colorimetrica è, tra i caratteri dello stimolo fisico,
quello corrispondente alla saturazione.
Alla ricezione di una radiazione complessa, comprendente per esempio radiazioni
delle due lunghezze d'onda λ1 e λ2, le luminanze si sommano, dando luogo a una
luminanza pari alla somma delle due luminanze; lo stesso avviene per il corrispondente carattere della percezione, la brillanza. Quanto ai due caratteri cromatici
della percezione (tinta e saturazione), essi sono definiti per convenzione in modo
tale che anche per essi, nel valutare gli effetti della composizione di più radiazioni,
si può operare per addizione.
Nel séguito considereremo, delle grandezze fotometriche, solo quelle dalle quali
dipende la sensazione di brillanza dei corpi osservati; tralasceremo invece la trattazione della colorimetria, limitandoci ad accennare a qualche aspetto legato alla colorazione delle sorgenti di luce artificiali.
6
APPUNTI DI FISICA TECNICA: FOTOMETRIA
1.4. Visione fotopica e visione scotopica
La rètina è diversamente sensibile agli stimoli luminosi nelle sue diverse parti, sia
per la non uniforme distribuzione delle cellule fotosensibili sulla sua superficie, sia
perché tali cellule, che sono di due diverse specie, hanno diverse risposte alla radiazione. Queste cellule sono i bastoncelli e i coni, così denominati per l'a spetto che
presentano all'osservazione al microscopio.
I bastoncelli sono distribuiti su tutta la superficie del fondo oculare; se colpiti dalla
radiazione luminosa, essi producono
uno stimolo nervoso capace di dare Corrispondenza tra la lunghezza d'onda
la percezione della luce, ma non del della radiazione monocromatica e il colore
percepito
colore. I bastoncelli sono attivi sollunghezze d'onda
colore
tanto se sono colpiti da radiazioni
380 400 nm
violetto
luminose non molto intense, tipiche
400 460 nm
cíano o índaco
della semioscurità notturna. Essi dan460
500
nm
azzurro
no luogo alla visione scotopica, così
500 560 nm
verde
detta dal gr. skótos (= oscurità). Oltre
560 580 nm
giallo
che dalla mancanza di discernimento
dei colori, la visione scotopica è ca580 610 nm
arancione
ratterizzata dalla lentezza dei pro610 780 nm
rosso
cessi di adattamento: passando dalla
luce piena alla semioscurità la visione
scotopica si attiva in alcune decine di minuti. Caratteristica della visione scotopica
è inoltre la scarsa definizione delle immagini in tutto il campo visivo.
Le cellule sensibili dell'altro tipo (i coni) sono distribuite sulla retina in modo non
uniforme: esse sono fittamente addensate nella regione centrale della retina (la fòvea) e sono molto più rade nelle zone periferiche. I coni sono i sensori attivi nella
visione fotopica (phôs = luce), quella che si ha in piena luce. La disuniformità della
distribuzione dei coni sulla retina è la causa della maggiore nitidezza con la quale
vengono distinti gli oggetti le cui immagini vengono a formarsi sulla fòvea, cioè
quelli verso i quali è direttamente rivolto lo sguardo, mentre ai bordi del campo visivo i contorni sono molto meno distinti e anche i colori sono percepiti meno chiaramente. Per questo motivo, pur se l'occhio normale è in grado di percepire immagini provenienti dal bordo del campo visivo fino a 104° dall'asse ottico, solo dirigendo lo sguardo direttamente su un oggetto se ne possono distinguere i particolari minuti. Caratteristiche della visione fotopica sono la possibilità di distinguere i
colori e la rapidità di adattamento all'intensità della radiazione, che è molto maggiore che nella visione scotopica.
Nella massima parte dei casi la luce comprende contemporaneamente radiazioni di
diverse lunghezze d'onda. Nel raro caso di una luce di una sola lunghezza d'onda
(radiazione monocromatica) vi è una diretta corrispondenza tra la lunghezza d'onda e il colore percepito dall'occhio normale, come indicato nello specchietto. Tale
corrispondenza viene a cadere nel caso di luce comprendente radiazioni di varie
1. LA FUNZIONE VISIVA
7
lunghezze d'onda: in tal caso il colore percepito è sempre dipendente dalle lunghezze d'onda che caratterizzano le radiazioni presenti, ma la corrispondenza non è immediata. Tra l'altro la sensazione di un dato colore può spesso essere ottenuta miscelando varie radiazioni monocromatiche, delle quali nessuna corrispondente al
colore voluto.
1.5. Curve normali di visibilità
In entrambi i modi di funzionamento della vista, fotopico e scotopico, l'occhio ha
una diversa sensibilità alle radiazioni elettromagnetiche delle varie lunghezze d'onda. Due sorgenti luminose di diverse lunghezze d'onda non danno mai luogo a sensazioni uguali, poiché saranno diverse almeno le due tinte percepite; a seconda
delle potenze, però, le due sorgenti possono avere la stessa brillanza. La radiazione
monocromatica che è capace, per data potenza, di destare la massima sensazione
luminosa nell'occhio umano (ossia quella che dà la massima brillanza) è quella
avente la lunghezza d'onda di 555 nm, la cui colorazione è giallo-verde.
Supponiamo di avere una sorgente monocromatica di lunghezza d'onda λ0 = 555
nm e potenza W0. Supponiamo poi di
disporre di un'altra sorgente monocromatica uguale alla precedente ma
avente lunghezza d'onda λ ≠ λ0 e potenza W variabile a piacere. Determiniamo il valore della potenza W
che la radiazione emessa dalla sorgente generica deve avere per destare, a parità di ogni altra condizione, la
stessa sensazione di brillanza. Denominiamo fattore di visibilità relativa
della radiazione di lunghezza d'onda Curve normali di visibilità. Curva F: visione fotoλ il rapporto:
pica; curva S: visione scotopica.
W
V (λ ) = 0 .
(1)
W
Questo rapporto, che per definizione è uguale a 1 per λ = λ0, è minore di 1 alle altre lunghezze d'onda; è uguale a zero alle lunghezze d'onda esterne all'intervallo
compreso tra 380 e 780 nm.
La figura presenta le curve normali di visibilità relative alla visione fotopica (curva
F) e alla visione scotopica (curva S). Sull'asse delle ascisse è la lunghezza d'onda λ
della radiazione monocromatica; nelle ordinate il fattore di visibilità relativa V(λ).
Il massimo della sensibilità dell'occhio (V(λ) = 1) si ha per la lunghezza d'onda λ =
λ0 = 555 nm in visione fotopica; a λ = 505 nm (verde) in visione scotopica. Ciò
vuol dire che la radiazione monocromatica che in piena luce dà, per data potenza, il
massimo di sensazione visiva è quella di colorazione giallo-verde, mentre in condi-
8
APPUNTI DI FISICA TECNICA: FOTOMETRIA
zioni di semioscurità tale massimo di sensibilità si sposta verso lunghezze d'onda
minori (fenomeno di Purkinje). Di solito ci si interessa solo della visione fotopica,
che è l'unico modo attivo nella massima parte delle applicazioni pratiche. Perciò
ordinariamente si considera la curva di visibilità F in visione fotopica, quando non
viene precisato diversamente.
Queste curve, ricavate da prove fatte su soggetti privi di disturbi della vista, sono
considerate dagli enti di unificazione come rappresentative della risposta dell'individuo normale alla radiazione visibile.
9
2. FOTOMETRIA
2.1. Generalità
La Fotometria ha lo scopo di fornirci i mezzi per calcolare e misurare gli effetti che
le onde elettromagnetiche hanno sull'occhio umano.
Da quanto detto al cap. 1 deriva che il campo d'interesse della Fotometria è limitato all'intervallo di lunghezze d'onda (nel vuoto) λ = 380 – 780 nm. Inoltre, considerando le diverse sensazioni che nell'uomo destano le radiazioni delle diverse lunghezze d'onda, è chiaro che, per la descrizione delle condizioni di luce esistenti in
un dato ambiente o delle caratteristiche possedute da una sorgente luminosa, non
basta riferirsi alle grandezze energetiche (energia, potenza, emittanza spettrale,
etc.). Perciò le grandezze usate in Fotometria sono definite al contempo sulla base
delle grandezze fisiche propriamente dette (potenza, frequenza) e delle caratteristiche della risposta dell'apparato visivo umano alle stesse grandezze (fattore V di visibilità relativa).
2.2. Grandezze fotometriche
2.2.1. Flusso luminoso
Una volta stabilita la curva di visibilità relativa V(λ), si può definire, in relazione a
una radiazione monocromatica di lunghezza d'onda λ assegnata e di potenza nota
W, la grandezza flusso luminoso:
Φ V = K MV (λ )W.
(1)
Si tratta, per la definizione, di una grandezza proporzionale alla potenza della radiazione. Il coefficiente V(λ), detto fattore di visibilità relativa, rende nullo il flusso ΦV per le lunghezze d'onda che sono al di fuori del campo di visibilità della radiazione; all'interno di tale campo tiene conto della diversa sensibilità dell'occhio
umano alle diverse lunghezze d'onda.
Il coefficiente KM è un fattore costante, che viene stabilito con la definizione dell'unità di misura del flusso luminoso. Nel sistema SI l'unità di misura del flusso luminoso è il lumen (lm) e il coefficiente KM ha, per la visione fotopica, il valore:
K M = 683 lm/W .
(2)
Una radiazione monocromatica di lunghezza d'onda λ = 555 nm e potenza pari a
1 W dà un flusso luminoso di 683 lm; se la sua lunghezza d'onda è diversa da 555
nm, il flusso luminoso sarà pari al prodotto 683 V(λ).
Per le radiazioni luminose nelle quali, come generalmente accade, siano presenti
più lunghezze d'onda, il flusso luminoso totale è dato dalla somma dei flussi luminosi. Così, se di una sorgente luminosa di superfi cie A, avente spettro di emissione
continuo, si conosce l'emittanza spettrale ε(λ), il flusso luminoso corrispondente è:
APPUNTI DI FISICA TECNICA: FOTOMETRIA
10
λ1
Φ V = AK M ∫ V( λ )ε( λ ) d λ.
(3)
λ0
I limiti d'integrazione λ0 e λ1 sono gli estremi del campo di visibilità della radiazione.
Con la definizione del fattore di visibilità relativa e della costante KM si stabilisce un legame tra le
grandezze fisiche e i fenomeni fisiopsicologici. Il flusso luminoso, assieme alle altre grandezze fotometriche che vedremo in séguito, pur essendo una grandezza di tipo fisico, rigorosamente definita e
misurabile, è tale da dare un'indicazione della capacità della radiazione di suscitare sensazioni luminose.
La corrispondenza così stabilita tra alcune grandezze fisiche e gli effetti psichici di queste si riferisce,
come detto, a individui in stato non patologico, e comunque vale solo in senso statistico. Tuttavia la
definizione delle grandezze fotometriche rende possibile progettare impianti di illuminazione, sorgenti
luminose etc., redigere capitolati, collaudare le opere realizzate e così via, facendo riferimento a grandezze fisiche esattamente definite.
In visione scotopica il fattore KM vale circa 1700 lm/W.
2.2.2. Intensità luminosa
La grandezza fotometrica fondamentale nel sistema di unità SI è l'intensità luminosa. Data una sorgente luminosa puntiforme P
(1), data altresì una semiretta n uscente da P verso
una certa direzione dello spazio, considerata una
regione dello spazio comprendente la semiretta e
vista dal punto P sotto l'angolo solido Ω, si dice
intensità luminosa di P verso la direzione n il limite verso il quale tende il rapporto tra il flusso luminoso ΦV emesso dalla sorgente verso quella regione dello spazio e l'angolo solido Ω, quando Ω
tende a zero:
Φ
dΦV
I V = lim V =
.
(1)
Ω →0 Ω
dΩ
Definizione dell'intensità lumiL'unità di misura è la candela. La candela è l'in- nosa.
tensità luminosa, in una determinata direzione, di
una sorgente che emette una radiazione monocromatica di frequenza 540 THz e la
cui intensità energetica (2) in quella stessa direzione è di 1/683 W/sr (la frequenza
di 540 THz corrisponde alla lunghezza d'onda nel vuoto di 555 nm).
La definizione dell'unità di misura dell'intensità luminosa per lungo tempo è stata fondata sull'uso di
una sorgente luminosa campione a combustione, originariamente una candela di forma, composizione
1
) Nella massima parte delle applicazioni una sorgente luminosa può essere considerata puntiforme
già a una distanza di 5–10 volte una dimensione caratteristica della sorgente stessa.
2
) V. nota seguente.
2. FOTOMETRIA
11
e dimensioni definite. Da qui venne il nome dell'unità, corrispondente al nome della candela nelle varie lingue (bougie, Kerz, candela, candle etc.).
In seguito il campione fu costituito dalla lampada campione Hefner, una lampada a stoppino di dimensioni assegnate capace, funzionando in condizioni esattamente definite (composizione del combustibile, pressione atmosferica, etc.), di fornire lungo una certa direzione una certa intensità luminosa.
Questa intensità luminosa fu presa come unitaria e denominata candela Hefner. Altri campioni di questo genere, basati sulla combustione di diverse sostanze, furono pure definiti e usati; tra questi, la candela a pentano (1909), detta anche candela decimale o candela internazionale. Furono anche stabiliti
dei campioni d'intensità luminosa costituiti da lampade elettriche a incandescenza, riproducenti la
candela internazionale, che furono depositati presso i laboratori ufficiali di alcuni stati.
Questi campioni d'intensità, leggermente diversi gli uni dagli altri, dettero luogo a unità di misura anche esse diverse tra loro; così la cande la Hefner equivale a 0,9 candele a pentano; la candela inglese a
1,01 candele a pentano.
Nel 1931 fu proposta e nel 1948 fu adottata dalla IX Conferenza Generale dei Pesi e delle Misure
(CGPM) una nuova unità di intensità luminosa, che si decise di indicare in tutte le lingue col nome latino di candela e col simbolo (cd). La candela fu definita come 1/60 dell'intensità luminosa emessa in
direzione normale da una superficie nera piana, estesa 1 cm2, che si trovi alla temperatura di solidificazione del platino alla pressione di 101325 Pa (cioè circa 2046 K). La candela definita in questo
modo risulta pari a circa 0,98 candele a pentano o decimali. La definizione della candela oggi legale in
Italia, quantitativamente equivalente a quella basata sul corpo nero, è quella stabilita nel 1979 dalla
XVI CGPM e già data sopra.
Dalla (1), integrando l'intensità luminosa su un angolo solido, si ottiene il flusso
luminoso ΦV:
d Φ V = I V d Ω;
(2)
Φ V = ∫ Ω I V d Ω.
Il flusso luminoso, di cui abbiamo visto la definizione al § 2.2.1, nel sistema SI è
una grandezza derivata ed è definita mediante la (2); l'unità del lumen risulta così
definita come il flusso luminoso emesso entro un angolo solido di uno steradiante
da una sorgente puntiforme isotropa avente l'intensità di una candela. Per una sorgente luminosa puntiforme isotropa, quindi con intensità luminosa IV uguale in tutte
le direzioni, dalle (2) si ricava:
Φ V = 4 πI V .
(3)
In passato l'indicazione del flusso luminoso emesso da una sorgente è stata data
talvolta per mezzo dell'intensità media sferica. Questa è l'intensità che avrebbe, in
una qualunque direzione, una sorgente isotropa che emettesse lo stesso flusso luminoso della sorgente data. Essa equivale al flusso luminoso diviso per 4π; si misura in candele medie sferiche. Tale unità di misura del flusso non è tra quelle comprese nel sistema SI.
Nel campo della trasmissione del calore per irraggiamento la grandezza energetica
che corrisponde alla grandezza fotometrica intensità luminosa è l'integrale, esteso
alla superficie emittente, dell'intensità dell'emittanza totale, la cui unità di misura è
il watt allo steradiante.
Consideriamo ora una sorgente luminosa estesa monocromatica di nota lunghezza
d'onda λ e di area A. Se essa ha verso una certa direzione l'intensità (energetica)
APPUNTI DI FISICA TECNICA: FOTOMETRIA
12
dell'emittanza j (1), la corrispondente
intensità luminosa è:
I V = AK MV (λ ) j.
(4)
Per una sorgente non monocromatica,
cioè emittente radiazioni di diverse
lunghezze d'onda, l'intensità luminosa
complessiva è calcolata come la somma delle intensità luminose relative alle
diverse λ. In simboli:
λ1
I V = AK M ∫ V( λ )
λ0
dj
d λ;
dλ
(5)
dove dj / dλ è l'intensità dell'emittanza spettrale alla lunghezza d'onda λ
nella direzione considerata.
Diagramma polare d'emissione di una sorUna caratteristica notevole di una sor- gente luminosa a simmetria assiale.
gente luminosa è la superficie fotometrica d'emissione, un diagramma polare spaziale che fornisce, per ogni direzione uscente dalla sorgente, l'intensità luminosa della sorgente nella stessa direzione.
Certe volte questo diagramma ha un asse di simmetria; in questi casi la superficie
fotometrica è definita dalla sua sola curva di intersezione con uno dei piani del
fascio definito dall'asse di simmetria. Si ottiene un diagramma polare come quello
della figura, dove l'intensità luminosa verso la direzione definita dall'angolo ϕ è data
dalla lunghezza del raggio uscente dal centro del diagramma L con anomalia ϕ.
Considerando le sorgenti estese, troviamo che una classe particolare di sorgenti luminose è costituita da quelle che seguono la legge di Lambert. L'intensità emessa
da tali sorgenti lungo una certa direzione dipende solo dall'angolo formato dalla
stessa direzione con la normale n secondo la relazione:
I V, ϕ = I V, n cos ϕ.
(6)
La superficie fotometrica perciò è una sfera tangente alla superficie emittente. IV, n
è l'intensità lungo la direzione normale; IV, ϕ è l'intensità lungo la direzione generica
considerata.
Nel caso di sorgenti la cui superficie fotometrica non presenti alcuna simmetria si
suole rappresentare tale superficie per mezzo di un numero adeguato di curve polari, ottenute come intersezioni con altrettanti piani, scelti in modo opportuno tra
quelli passanti per il centro della lampada L.
1
) Spesso in fotometria è conveniente supporre una sorgente puntiforme. In questo caso al posto del
prodotto Aj si deve considerare un'altra variabile energetica opportunamente definita, la cui unità di
misura è il watt allo steradiante. Di solito anche tale variabile è detta intensità energetica, ma non la si
deve confondere con la variabile j.
2. FOTOMETRIA
13
2.2.3. Radianza
Di una sorgente luminosa estesa si definisce la radianza o emittanza luminosa, qui
indicata col simbolo MV. La radianza in un punto è il limite del rapporto tra il flusso luminoso emesso da una porzione della superficie emittente, comprendente il
punto considerato, e l'area della stessa superficie, quando l'area tende a zero:
Φ
dΦV
M V = lim V =
.
(1)
A→0 A
dA
È la grandezza fotometrica corrispondente all'emittanza integrale J che si definisce
nello studio della trasmissione del calore per irraggiamento.
L'unità di misura della radianza è il lumen al metro quadrato (lm/m2).
2.2.4. Luminanza
Per le sole sorgenti estese si definisce la luminanza LV. Luminanza di una sorgente
in un suo punto e verso una determinata direzione dello spazio, che formi l'angolo
ϕ con la direzione normale alla superficie emittente, è il limite del rapporto tra l'intensità luminosa emessa in quella direzione da una porzione di superficie comprendente il punto considerato e l'estensione apparente della stessa superficie, vista dalla stessa direzione, quando tale estensione tende a zero:
d IV
dΦV
dMV
IV
=
=
=
.
LV = lim
(1)
A→ 0 A cos ϕ
d A cos ϕ d Ω d A cos ϕ d Ω cos ϕ
L'unità di misura della luminanza è la candela al metro quadrato (cd/m2), unità denominata nit (nt).
In passato si è usato anche lo stilb, pari a 1 cd/cm2 ossia 104 cd/m2.
Un'altra unità di misura talvolta ancora usata è il lambert, che è la luminanza di una superficie lambertiana di 1 cm2 che emette un flusso
luminoso di 1 lm. Vale la relazione:
104 cd
(2)
.
π m2
L'unità del sistema inglese è il footlambert (fL), pari alla luminanza di
una superficie lambertiana estesa 1 ft2 che emette un flusso luminoso
di 1 lm. Vale la relazione:
cd
(3)
1 fL = 3,426 2 .
m
1 lambert =
Per una sorgente lambertiana la (1) dà, qualunque sia la direzione considerata:
d I V, n
LV, ϕ = costante =
;
(4)
dA
cioè le sorgenti luminose lambertiane hanno luminanza costante in tutte le direzioni.
APPUNTI DI FISICA TECNICA: FOTOMETRIA
14
Dalla definizione della radianza e dalla (1) si ricava (1):
M V = ∫ LV cos ϕ d Ω = πLV .
(5)
2π
Si può dimostrare
Alcuni valori di luminanza
che una sorgente di
superficie
del
Sole
vista
dalla Terra
1,6×109 cd/m2
radiazione lamberarco elettrico
1×108 cd/m2
tiana, la cui comfilamento di tungsteno di lampada a incande5×106 cd/m2
posizione spettrale
scenza
non dipenda dalfilamento di carbone di lampada a incande8×105 cd/m2
l'angolo ϕ, è pure
scenza.
foglio di carta illuminato in pieno sole
3×104 cd/m2
una sorgente lumilampada fluorescente tubolare da 40 W
4500 cd/m2
nosa lambertiana,
3
cielo sereno di giorno
10 104 cd/m2
ossia obbedisce alfiamma
(1 – 2)×104 cd/m2
la (6) del § 2.2.2.
superficie della Luna vista dalla Terra
2500 cd/m2
cielo nuvoloso di giorno
50 – 500 cd/m2
Per un'idea dei vacielo sereno con luna di notte
102 – 101 cd/m2
lori di luminanza di
soglia di luminanza percepibile
≈106 cd/m2
alcune tra le più
comuni sorgenti luminose si considerino i valori esposti nello specchietto del riquadro. Si osservi pure
l'estensione del campo dinamico dell'occhio umano, considerato come un trasduttore: il rapporto tra l'estremo superiore di luminanza osservabile e la soglia di sensibilità, rispettivamente
uguali a 106 e
Alcuni valori di illuminamento su piano orizzontale
106 cd/m2, è di ben
105 lx
in pieno sole, cielo sereno, sole 50° sull'orizzonte
1012, cioè 120 dB.
in piena luce diffusa dal cielo sereno
5×104 lx
La visione fotopica
di giorno con cielo coperto
104 lx
è pienamente attiva
all'interno con illuminazione artificiale
100 − 104 lx
quando l'occhio si
di notte con luna piena
0,2 lx
è adattato a una ludi notte senza luna
10-2 lx
minanza del campo
osservato superiore a circa 3 cd/m2; la visione è del tipo scotopico quando l'occhio
si è adattato a una luminanza di circa 103 cd/m2 o inferiore.
2.2.5. Illuminamento
Passiamo a considerare le superfici illuminate. In relazione a queste si definisce l'illuminamento EV in un punto, limite del rapporto tra il flusso luminoso ΦV, inc. incidente su una superficie e l'area S della superficie per S tendente a zero:
1
) La (5) è strutturalmente uguale alla relazione esistente tra l'emittanza integrale J e l'intensità normale jn (v. Fisica Tecnica 1 Trasmissione del calore, § 4.2, eq. 9): J = πjn.
2. FOTOMETRIA
EV =
15
d Φ V, inc .
.
dS
Nel sistema SI l'unità di misura è il lux (lx):
lm
1 lx = 1 2 .
m
(1)
(2)
L'unità del sistema inglese è il lumen al piede quadrato o footcandle (fc):
1
lm
=
= 10,764 lx .
2
0,30482 m2
ft
Altra unità ancora è il phot = 1 lm/cm2 = 104 lx.
1 fc = 1
lm
(3)
Nella tabella vengono dati alcuni valori d'illuminamento tipici riferiti a un piano orizzontale.
Se gli oggetti presenti nell'ambiente e osservati
hanno dei valori del coefficiente di riflessione
non troppo bassi, si può dire che la visione
fotopica si ha in presenza di valori di illuminamento ≥10 lx, mentre per valori compresi
tra 103 e 106 lx è attiva la visione scotopica.
Nel campo intermedio, tra 103 e 10 lx, si ha la
visione mesopica, nella quale sono contemporaneamente attivi i due modi.
Vediamo come può essere calcolato l'illuminamento prodotto da una sorgente luminosa su
una superficie. Una superficie elementare dS
Flusso luminoso inviato da una sorsia illuminata da una sola sorgente puntiforme P gente puntiforme su una superficie
posta alla distanza R. Della sorgente sia noto il infinitesima (sopra) e su una superdiagramma polare fotometrico di emissione. Da ficie finita (sotto).
questo si ricava il valore dell'intensità luminosa
IV emessa dalla sorgente nella direzione della superficie dS. Il flusso luminoso incidente sulla superficie dS è dato da:
d Φ V, inc. = I V d Ω S = I V
dS
R2
cos ϕ S
(4)
e il corrispondente illuminamento è:
d Φ V, inc . I V
EV =
= 2 cos ϕS .
(5)
dS
R
Se la superficie illuminata è estesa, l'illuminamento su di essa sarà in generale variabile da un
punto all'altro, poiché IV, R e ϕS variano con lo
spostarsi del punto considerato sulla superficie
S. Il flusso incidente su S è allora:
Flusso luminoso inviato dalla sorgente elementare dA verso l'elemento dS.
APPUNTI DI FISICA TECNICA: FOTOMETRIA
16
Φ V, inc . = ∫ I V d Ω S = ∫
IV
cos ϕS d S .
(6)
R2
Consideriamo il caso che la sorgente luminosa sia estesa. Se essa è lambertiana,
abbiamo tra due elementi di superficie dA emittente e dS illuminata:
M V, A cos ϕ A cos ϕS
d Φ V, inc . = d I V d ΩS = LV, A cos ϕ A d A =
d A d S.
(7)
π
R2
Integrando sulle due superfici, troviamo l'espressione del flusso luminoso complessivamente inviato dalla sorgente A sulla superficie S:
cos ϕ A cos ϕS
Φ V, inc . = M V, A ∫ ∫
d A d S = M V, A AFAS ;
(8)
πR 2
AS
dove FAS è il fattore di forma da A ad S, definito come per i calcoli di trasmissione
del calore per irraggiamento.
S
S
2.3. Sorgenti secondarie
Un corpo che riceva una certa radiazione elettromagnetica ne rinvia una frazione pari al proprio
coefficiente di rinvio. Tale coefficiente è una funzione della lunghezza d'onda; perciò la radiazione
incidente e quella rinviata differiscono, oltre che
per la potenza, anche per la composizione spettrale. La proprietà di un corpo di rinviare in misura
maggiore o minore le radiazioni delle diverse lunghezze d'onda è quella che, quando il corpo sia illuminato da luce bianca, fa sì che un osservatore
percepisca il corpo stesso come colorato.
Considerazioni simili possono farsi in relazione alla
radiazione che, incidendo su un corpo non opaco,
Definizione di r e t.
lo attraversa e ne esce fuori dall'altro lato.
In entrambi i casi (rinvio e trasmissione della radiazione) il corpo può essere considerato esso stesso a propria volta come una sorgente luminosa: una sorgente secondaria.
Anche una sorgente secondaria può seguire la legge di Lambert o avere invece, in
misura maggiore o minore, caratteristiche direzionali. Come esempi di sorgenti secondarie lambertiane possiamo pensare al gesso, a un vetro traslucido, a una superficie piana ricoperta da uno strato liscio di pittura non lucida.
Sia A la superficie, ΦV, inc. il flusso luminoso incidente, EV = ΦV, inc./A l'illuminamento, supposto uguale su tutta la superficie. Se è r il coefficiente di riflessione
diffusa (albedo), il flusso rinviato è:
Φ V, r = rΦ V, inc .
(1)
2. FOTOMETRIA
17
e la radianza:
Φ V, r rΦ V, inc .
MV =
=
= rEV .
(2)
A
A
Poiché la superficie è lambertiana, la luminanza è:
I V, n
M
r
LV = V = E V =
(3)
π
π
A
e l'intensità lungo una direzione che forma l'angolo ϕ con la normale è:
r
I V, ϕ = I V, n cos ϕ = LV A cos ϕ = EV A cos ϕ.
(4)
π
Nel caso di una sorgente secondaria funzionante per trasparenza le stesse relazioni
possono essere riscritte sostituendo al fattore r il coefficiente t di trasmissione.
2.4. Misura delle grandezze fotometriche
2.4.1. Illuminamento
L'illuminamento EV può essere misurato per
mezzo di celle fotovoltaiche (luxmetri o luxometri), essenzialmente costituiti da un sensore
S a semiconduttore nel quale, quando esso sia
colpito da luce, si genera una forza elettromotrice (e); questa viene misurata con un voltmetro G.
Se la risposta dello strumento fosse indipendente dalla lunghezza d'onda della radiazione,
la forza elettromotrice suscitata nella cella sarebbe approssimativamente proporzionale alla
Misura dell'illuminamento con una
potenza della radiazione elettromagnetica assorbita dalla superficie sensibile e il dispositivo cella fotovoltaica.
costituirebbe un misuratore di potenza radiante
o radiometro. Invece per avere un misuratore di flusso luminoso bisogna che la
curva di sensibilità alla radiazione dello strumento riproduca la curva di visibilità
normale della luce in modo che, per una radiazione incidente monocromatica di
lunghezza d'onda λ e potenza W(λ), valga la relazione:
e
= s (λ ) = CV (λ )
(1)
W (λ )
dove W(λ) è la potenza della radiazione monocromatica incidente sul sensore,
s (λ), sensibilità, è il rapporto tra la forza elettromotrice generata e la potenza della
radiazione, V(λ) è la visibilità relativa della radiazione, funzione della sua lunghezza
d'onda, C una costante caratteristica dello strumento indipendente da λ. All'esterno
18
APPUNTI DI FISICA TECNICA: FOTOMETRIA
del campo di visibilità della radiazione la risposta del sensore deve ovviamente essere nulla.
In generale la condizione (1) non è rispettata dal sensore se non approssimativamente; per rimediare, si pongono sul sensore dei filtri che possano attenuare quelle
componenti della radiazione che altrimenti darebbero luogo a una risposta eccessiva del sensore; così si ottie ne, più o meno esattamente, il rispetto della condizione (1) da parte dell'insieme (filtro + sensore). Per semplicità di uso, il voltmetro
porta una scala direttamente tarata in lux.
Sono usati altri luxometri, che si fondano su diversi principi di funzionamento: ve
ne sono a fotoresistenza, a fotodiodo, etc.
2.4.2. Intensità luminosa
Può essere misurata in vari modi, che si riconducono all'uno o all'altro dei due metodi che qui di seguito consideriamo.
Il primo metodo, che è stato anche il primo applicato storicamente, si basa sul giudizio di un osservatore per un confronto tra l'intensità da misurare e una intensità di
riferimento conosciuta. Si dispongono come nella figura la sorgente luminosa L da
sottoporre a misura, la sorgente campione C, che serve da riferimento, e un piccolo
schermo S che, illuminata da un lato dalla sorgente C e dall'altro da L, assume a sua
volta due valori di luminanza, che possono essere confrontati. Tutto il dispositivo è
posto in camera oscura, cosicché non vi sia il disturbo della luce proveniente da altre sorgenti.
Se l'angolo solido Ω 1, sotto il quale lo schermo S è visto dalla sorgente C, è abbastanza piccolo, l'illuminamento della faccia di sinistra dello schermo S, causato
dalla sorgente L posta alla distanza R1, è:
I Ω
I A I
Φ
EV 1 = 1 ≈ V 1 1 ≈ V 1 2 = V21
(1)
A
A
AR1
R1
dove A è l'area dello schermo S e IV1 è
l'intensità della sorgente C nella direzione di S. Lo schermo è costituito da
una superficie bianca lambertiana (un
foglio di carta, uno strato di gesso, o
simile superficie); se r è la sua albedo
(coefficiente di riflessione diffusa), essa costituisce a sua volta una sorgente
di luminanza pari a rEV1/π (v. § 2.3).
fotometrico per la misura dell'intensità
Lo stesso può dirsi, sotto simili condi- Banco
luminosa col metodo del confronto.
zioni, per il lato illuminato dalla sorgente L, che riflette con luminanza pari
a:
2. FOTOMETRIA
19
rE V 2 I V 2
= 2 .
(2)
π
R2
Regolando le due distanze R1 e R2 opportunamente, si può fare in modo che le due
luminanze siano uguali. Una volta raggiunta tale condizione, è:
I V1 I V 2
= 2 .
(3)
R12
R2
In questa relazione IV2 è nota; le distanze R sono facilmente misurabili; così è determinabile la IV1.
Ora bisogna chiarire come può essere individuata la condizione di pari luminanza
dei due lati dello schermo S. L'occhio è sensibile alla luminanza delle superficie (v.
§ 2.1), ma non ha la capacità di paragonare le luminanze di due sorgenti che siano
osservate in tempi successivi; perciò i due lati dello schermo devono essere osservati contemporaneamente. Ciò può essere fatto in vari modi, a seconda del fotometro impiegato: per esempio, mediante un sistema di specchi.
Con questo procedimento può risultare
difficile giudicare della uguaglianza di due
luminanze, se si tratta di luci aventi colorazioni molto diverse. In casi di tal genere
si può effettuare una catena di passaggi
con sorgenti di colorazioni intermedie,
confrontando una sorgente con la successiva, fino alla lampada campione.
Il fatto che la valutazione dell'intensità si
fonda sul giudizio dell'operatore causa pe- Misura dell'intensità luminosa con l'uso di un
rò qualche incertezza nella misura. Oggi luxmetro.
generalmente si preferisce seguire un altro
metodo, che si fonda sull'uso di un luxmetro per misurare l'illuminamento prodotto
su una superficie posta a una certa distanza dalla sorgente in posizione perpendicolare al raggio uscente dalla sorgente nella direzione nella quale si vuole misurare
l'intensità. Se la sorgente è abbastanza piccola e la distanza R è abbastanza grande,
per l'intensità luminosa sul ricevitore si può scrivere:
ΦV Φ V R2
=
≈ EV R 2 .
(4)
Ω
A
La distanza R è facilmente misurabile; l'illuminamento EV è rilevato con un luxmetro.
Generalmente l'attrezzatura per la misura dell'intensità luminosa comprende un
banco fotometrico, cioè un'asta rettilinea molto rigida e stabile, su cui sono scorrevoli i supporti della lampada da esaminare e il luxometro. Tutto il sistema è collocato in camera oscura, affinché le misure non siano influenzate da sorgenti luminose estranee. Spesso il supporto della sorgente da esaminare è girevole in modo
IV ≈
20
APPUNTI DI FISICA TECNICA: FOTOMETRIA
da permettere con facilità la ripetizione della misura lungo diverse direzioni. Così si
può determinare il diagramma polare dell'intensità luminosa o superficie fotometrica di emissione della sorgente (v. § 2.2.2).
2.4.3. Luminanza
Consideriamo una sorgente luminosa estesa, della quale vogliamo
misurare la luminanza nel punto P
lungo una certa direzione. Lungo
questa direzione e alla distanza R
disponiamo uno strumento apposito, detto luminanzometro, essenzialmente costituito da una camera
recante una finestrella F di area SF;
sul fondo è una cella C, del tipo
usato per i luxometri, misurante il
flusso luminoso incidente su di essa.
Le pareti laterali del contenitore sono internamente molto assorbenti
(nere), sicché il flusso luminoso che
arriva sulla cella C è solo quello diSchema del luminanzometro.
rettamente proveniente dalla porzione della superficie A delimitata
dall'angolo solido Ω M, dipendente dalle dimensioni dello strumento.
Se l'area su cui punta lo strumento emette nella direzione della finestra con intensità
IV, il flusso luminoso che entra nello strumento e viene a cadere sulla cella di misura C è:
Φ V = I V Ω F = LV A cos αΩ F ;
(1)
se Ω F è il piccolo angolo solido sotto il quale da ogni punto della superficie A si
vede la finestra F. Per tale angolo solido si può scrivere:
S
Ω F ≈ F2 .
(2)
R
Poiché anche l'angolo solido Ω M è sempre piccolo, vale pure la relazione:
A cos α ≈ Ω M R 2
(3)
con α l'angolo formato dalla normale n ad A con la retta passante per la finestra SF.
Dalle (1), (2), (3) si trova:
S
Φ V = LV A cos αΩ F = LV Ω M R 2 F2 = LV S F Ω M .
(4)
R
La (4) lega il flusso luminoso ΦV misurato con la cella C e la luminanza LV della
superficie verso cui è puntato il luminanzometro; le altre grandezze che figurano
2. FOTOMETRIA
21
nella (4), SF e Ω M, sono caratteristiche solo dello strumento; di esse si può tenere
conto una volta per tutte nella taratura della scala di lettura dello strumento indicatore, che dà direttamente il valore della luminanza in candele al metro quadrato.
Se la superficie emittente è lambertiana, il valore della luminanza non muta al variare dell'angolo α, altrimenti LV dipende dalla direzione di osservazione.
Lo strumento descritto ha la stessa struttura di un esposimetro per riprese fotografiche. A differenza
del sensore C di un luminanzometro, la cella di misura di un esposimetro dovrebbe avere una curva di
sensibilità s (λ) riproducente, invece della curva normale di visibilità dell'occhio umano V(λ), la curva
di sensibilità spettrale della pellicola fotografica impiegata, che si discosta più o meno dalla V(λ). Inoltre in un esposimetro fotografico lo strumento indicatore fornisce, invece del valore della luminanza,
l'indicazione del tempo di esposizione e dell'apertura della lente da usare per l'esposizione; la taratura
della scala è facilmente modificata in funzione della sensibilità della pellicola usata. Nel caso di un
apparecchio automatico il segnale elettrico fornito dalla cella non è presentato per la lettura, ma viene
usato come segnale d'ingresso per il dispositivo che stabilisce i parametri per l'esposizione: apertura
dell'obiettivo e tempo di esposizione.
2.4.4. Flusso luminoso
La misura diretta del flusso luminoso emesso da una lampada con superficie fotometrica qualunque può essere fatta con un apposito strumento: la sfera di Ulbricht.
Questa è una sfera cava avente un diametro di qualche metro e la superficie interna
ricoperta da una adatta vernice che la rende bianca e diffondente (lambertiana), almeno nel campo della radiazione visibile.
All'interno della sfera viene collocata, in
posizione eccentrica, la sorgente L da sottoporre a misura. Nella superficie della sfera è aperta una finestrella F di area SF; un
piccolo schermo P impedisce che la luce emessa da L venga direttamente a colpire la
finestra F. Sulla superficie di questa, dalla
parte interna, si produce un illuminamento
EF per effetto della riflessione diffusa della
luce emessa da L sulla parete interna della
sfera e delle successive riflessioni che la luce subisce ulteriormente sulla parete stessa.
La sfera di Ulbricht.
Tale illuminamento è proporzionale al flusso ΦL emesso dalla sorgente L. Per chiarire
ciò, consideriamo l'elemento di superficie dSF sulla finestra e in particolare l'effetto
su di essa della prima riflessione della luce su un generico elemento infinitesimo di
parete esteso dA. Su questo incide una parte infinitesima del flusso ΦL emesso da
L, che indichiamo con dΦA. Se è r l'albedo della superficie dA, il flusso rinviato da
questa è pari a:
d Φr = r d ΦA .
(1)
APPUNTI DI FISICA TECNICA: FOTOMETRIA
22
Lungo la direzione della retta uscente dall'areola dA e passante per F l'intensità luminosa è, per la legge di Lambert:
dΦr
dII =
cos ϕ
(2)
π
e corrispondentemente il flusso luminoso incidente sull'area dSF è:
d S F cos ϕ
d ΦI = d I I
(3)
(2 R cos ϕ)2
dove R è il raggio della sfera. Combinando con le eqq. (2) e (1) si ottiene:
d Φr d SF
d SF
= r d ΦA
d ΦI =
.
(4)
2
π 4R
4 πR 2
Come si vede, l'espressione ottenuta non dipende dalla posizione dell'area dA sulla
superficie sferica, ma solo dall'albedo r, dal rapporto tra l'area della finestrella e
quella della sfera e dal flusso luminoso dΦA incidente sull'elemento dA. Sommiamo
ora tutti i contributi al flusso luminoso su dSF provenienti dagli elementi di area
come dA. Ricordando che è:
ΦL = ∫ IV d Ω = ∫ d ΦA;
(5)
4π
sfera
troviamo il flusso incidente su dSF dopo la prima riflessione e il relativo illuminamento:
d SF
rΦ L ;
(6)
dΦI =
4 πR 2
d ΦI
r
I
=
ΦL.
(7)
EV =
d S F 4 πR 2
Questo valore non dipende dalla posizione occupata dalla finestra sulla superficie
sferica né dalla posizione della lampada all'interno. Osserviamo ancora che la superficie sferica, così illuminata al pari di d SF, costituisce essa stessa una sorgente di
luce di flusso r ΦL, che, analogamente a quanto visto sopra, produce sulla finestra
un illuminamento:
r2
=
ΦL.
(8)
4 πR 2
Poiché le stesse considerazioni possono essere ripetute ancora per le infinite riflessioni che la luce subisce sulla superficie interna della sfera, l'illuminamento complessivo sull'elemento di superficie dSF e su tutta la finestra F è dato dalla somma:
Φ
E F = r L 2 1 + r + r 2 + r 3 + ...
(9)
4 πR
Osservando che è r < 1 e che quindi la serie in parentesi converge a 1/(1-r ), l'illuminamento complessivo sulla finestra risulta:
EVI I
(
)
2. FOTOMETRIA
23
r ΦL
(10)
.
1 − r 4 πR 2
Questa è la relazione tra il flusso luminoso emesso dalla lampada esaminata e l'illuminamento sulla finestra F, relazione che è bene verificare tarando la sfera di Ulbricht per mezzo di una lampada campione, di cui si conosca con precisione il flusso luminoso.
Quanto alla misura di EF, questa può essere
eseguita collocando nella finestra il sensore
di un luxometro, ovviamente rivolto verso
l'interno della sfera. Un'altra via è quella di
chiudere la finestra con uno schermo traslucido, costituito da vetro smerigliato o altro
simile materiale, di noto coefficiente di trasmissione t. Lo schermo, ricevendo dall'interno il flusso luminoso EF SF, emette verso
l'esterno il flusso tEFSF con una radianza:
M V = tE F .
(11)
Se lo schermo è, in relazione alla radiazione
trasmessa, una sorgente secondaria lamberCalcolo del flusso luminoso emesso da
tiana, basterà misurare la sua intensità lumi- una sorgente simmetrica rispetto a un
nosa emessa in direzione normale IN per po- asse.
tere calcolare l'illuminamento EF sulla faccia
interna; infatti in tal caso si avrà:
M
π IN
.
(12)
EF = V =
t
t SF
Un altro metodo per valutare il flusso luminoso emesso da una sorgente è quello di
calcolarlo, quando sia noto il diagramma polare di emissione della sorgente, per
mezzo della definizione:
Φ V = ∫ I V d Ω.
(13)
EF =
4π
Il calcolo numerico può essere fatto in modo semplice per quelle sorgenti che, come gran parte di quelle comunemente in uso, hanno una superficie fotometrica di
emissione simmetrica rispetto a un asse. Per effettuare l'integrazione numerica cominciamo col tracciare, con centro in L, una semicirconferenza di raggio R; consideriamo poi due rette uscenti da L con angoli ϕA e ϕB e l'angolo solido ∆Ω compreso tra i due coni da esse definiti. Indicando con s la lunghezza del segmento AB,
congiungente le proiezioni sull'asse delle intersezioni delle due rette con la circonferenza di raggio R e con S la superficie del segmento sferico corrispondente, si
ha:
S
2πRs
s
∆Ω ≈ 2 = 2 = 2π = 2 π(cos ϕ A − cos ϕ B ).
(14)
R
R
R
24
APPUNTI DI FISICA TECNICA: FOTOMETRIA
Si trova:
2π
(15)
∑ ( I V S )i
R i
i
4π
con la sommatoria estesa a tutti i segmenti come AB nei quali risulta diviso il diametro dalle proiezioni su di esso dei punti di intersezione della circonferenza con i
raggi uscenti da L. Se gli angoli ϕ sono scelti in modo che le aree Si degli n segmenti sferici ottenuti risultino tutte uguali, e quindi siano uguali le lunghezze di
tutti i segmenti staccati sul diametro, allora è:
4π
4π
∆Ω =
;
ΦV =
(16)
∑ I V, i .
n
n i
Φ V = ∫ I V d Ω ≈ ∑ ( I V ∆Ω)i =
2.5. Temperatura di colore
È noto (legge di Wien per il corpo nero) che un corpo ad alta temperatura emette
una radiazione luminosa, il cui colore è legato alla temperatura del corpo. Infatti i
corpi, che a freddo non sembrano emettere radiazioni, se vengono scaldati a temperature crescenti appaiono via via più luminosi, mentre la tinta della luce emessa
va cambiando. Tale fenomeno permette la valutazione approssimata della temperatura del metallo arroventato, che si fa correntemente, per es., nella lavorazione
artigianale dell'acciaio. Esso è anche alla base di un metodo per indicare il colore di
una sorgente, che è quello di darne la temperatura di colore: questa è la temperatura alla quale la radiazione del corpo nero ha la stessa tinta della luce emessa
dalla sorgente considerata.
Perché il concetto della temperatura di colore possa essere applicato a una certa
radiazione, è necessario che la sua tinta si avvicini a una delle tinte assunte dalla
radiazione del corpo nero alle diverse temperature. Queste tinte sono in pratica
quelle della luce emessa dal filamento di una lampada a incandescenza ossia, per T
crescenti, dal rosso nascente al rosso vivo all'arancione al bianco giallastro. Per
temperature superiori sono il bianco della luce solare (≈5000 K) fino al bianco-azzurro (≈10 000 K).
Nel caso dell'emissione di corpi neri o grigi la temperatura di colore è, per la definizione, pienamente in grado di indicare la tinta della luce. Con le sorgenti termiche
selettive (non grigie) e con gran parte delle lampade a fluorescenza il metodo è ancora idoneo a dare un'indicazione abbastanza significativa del colore. Invece con le
sorgenti di luce colorata (lampade a vapori di sodio, lampade a scarica colorate per
insegne commerciali etc.) il metodo della temperatura di colore non è applicabile.
25
3. SORGENTI DI LUCE
3.1. Generalità
La sorgente naturale di luce è il Sole. La sua radiazione, così come arriva al la superficie terrestre, ha una distribuzione spettrale che si avvicina in qualche modo a
quella di un corpo nero alla temperatura di ≈ 5000 K. Nel campo delle radiazioni
visibili e ultraviolette e in larghe bande della radiazione infrarossa la potenza spettrale della radiazione solare è però inferiore a quella del corpo nero, specialmente
in corrispondenza con le bande di assorbimento caratteristiche delle molecole di
O2, N2, H2 O, O3, CO2, che sono le specie chimiche, tra quelle presenti nell'atmosfera, che determinano un più forte assorbimento delle relative componenti
spettrali.
La temperatura di colore della radiazione solare è di ≈5000 K quando il Sole è allo
Zenit; si abbassa quando il Sole ha una minore altezza sull'orizzonte fino ai momenti dell'alba e del tramonto, quando la colorazione della luce solare è nettamente
rossastra. La curva normale di visibilità dell'occhio umano in visione fotopica è ben
adatta a tale composizione spettrale; infatti essa ha il massimo per λ = 555 nm, che
corrisponde al massimo dell'emittanza spettrale del corpo nero alla temperatura di
5225 K.
Nei luoghi all'aperto in ombra, ossia al riparo dalla radiazione solare diretta, la luce
solare arriva dopo aver subito la riflessione diffusa attraverso l'atmosfera e sui corpi circostanti. La composizione spettrale di questa radiazione è variabile a seconda
della presenza di pulviscolo e nubi nell'aria e risente anche della presenza di edifici,
monti, alberi etc. In generale la luce solare indiretta ha una colorazione che tende
all'azzurro e la sua temperatura di colore è superiore a quella della radiazione diretta.
In generale ogni sorgente artificiale di luce dovrebbe tendere alla temperatura di
colore della luce solare diretta, poiché in questo modo la visione che se ne ottiene
dà la gradevole sensazione della luce naturale. Però si nota che, quando l'illuminamento ha valori bassi, come accade spesso negli ambienti interni con illuminazione artificiale, può riuscire più gradevole una luce più rossastra, cioè di minore
temperatura di colore (è quella che invece si suole indicare, in linguaggio corrente,
come luce più calda!).
Uno dei principali parametri che definiscono le prestazioni di una sorgente di luce
artificiale è il rendimento luminoso, dato dal rapporto tra il flusso luminoso emesso e la potenza fornita. Per il rendimento luminoso si adotta il simbolo ηV:
Φ
ηV = V .
(1)
W
La sua unità di misura è il lumen al watt. Il valore massimo teorico è di 683 lm/W.
Gli altri parametri più importanti di una sorgente sono:
- il flusso luminoso;
26
APPUNTI DI FISICA TECNICA: FOTOMETRIA
- la luminanza, da cui dipende l'eventuale verificarsi dell'effetto di abbagliamento;
- la temperatura di colore.
3.2. Lampade a incandescenza
Vengono così chiamate, escludendo le lampade a incande scenza per combustione,
le lampade costituite da un'ampolla di vetro racchiudente un filamento metallico incandescente per effetto della corrente elettrica che lo percorre. L'emissione del filamento è regolata dalla legge di Planck, trattandosi, generalmente, di un materiale
assimilabile a un corpo nero o a un corpo grigio di alta emissività.
Il problema posto da tali lampade è quello, già accennato, del rendimento luminoso.
Il filamento emette in tutto lo spettro, per λ compreso tra 0 e ∞; la curva di emissione spettrale ha un massimo per la lunghezza d'onda λmax data dalla legge di
Wien:
2,9 × 106
λ max =
(1)
nm
T
Allontanandoci da tale valore di λ, troviamo che l'emittanza spettrale decresce fino
al valore zero per λ → 0 e per λ → ∞. Perché il massimo venisse a cadere alla lunghezza d'onda λ = 555 nm, cioè nelle migliori condizioni di visibilità della radiazione, la temperatura del filamento dovrebbe essere pari a 5225 K. Tale temperatura
però è troppo elevata per qualsiasi materiale; perciò nella pratica il massimo dell'emittanza spettrale ε(λ) di una lampada a incandescenza è sempre compreso nel
campo della radiazione infrarossa.
Le prime lampade elettriche a filamento di carbone funzionavano a circa 1800°C, non potendosi
andare a temperature superiori per evitare una
troppo rapida distruzione del filamento per sublimazione. A questa temperatura il massimo
dell'emittanza spettrale ε0 (λ) del corpo nero è
situato a λ ≈ 1400 nm, mentre nel campo della
radiazione visibile è compresa solo una piccola
parte dell'energia irradiata.
Le lampade a filamento di carbone lavoravano
con bassissime pressioni nell'ampolla. Da questa,
infatti, si estraeva l'aria per quanto possibile per
ritardare l'ossidazione del carbonio del filamento
Emittanza spettrale del corpo nero a varie
e la conseguente rottura del filamento stesso. Però
temperature. La zona retinata segna l'intervallo
la bassa pressione aveva, insieme con l'alta temdi lunghezze d'onda della radiazione visibile
peratura, l'effetto di accelerare la sublimazione
del carbonio; questo poi si andava a depositare
sulla superficie interna dell'ampolla di vetro, annerendola. Questo fatto costituì una s eria difficoltà,
che impedì per lungo tempo di innalzare molto la tempe ratura di funzionamento del filamento, finché
non si poté adottare il filamento di tungsteno.
L'uso del wolframio metallico o tungsteno per fabbricare il filamento fu possibile
quando si misero a punto le tecniche necessarie per lavorare questo materiale in fili
3. SORGENTI DI LUCE
27
abbastanza sottili per ottenere la desiderata resistenza elettrica e al contempo abbastanza robusti meccanicamente perché fossero praticamente utilizzabili. Oggi il
tungsteno è quasi l'unico materiale conduttore usato per i filamenti delle lampade,
soprattutto perché ha un alto punto di fusione (circa 3400°C) e può essere usato
senza gravi problemi anche alla temperatura di 2800°C. Il rendimento luminoso risulta così au mentato, anche per una certa selettività dell'emissione termica del
tungsteno, che favorisce le lunghezze d'onda comprese nel campo della radiazione
visibile rispetto alle altre.
Con l'uso del tungsteno e praticando il vuoto nell'ampolla si verifica l'inconveniente
della sublimazione del metallo e della sua condensazione sul vetro. Si rimedia riempiendo l'ampolla di un adatto gas chimicamente inerte, che ritarda il processo di
sublimazione del wolframio metallico anche se, così facendo, vie ne ad attivarsi una
certa trasmissione del calore per convezione tra il filamento e il vetro; il conseguente abbassamento della temperatura del filamento ha l'effetto di abbassare un
po' il rendimento luminoso. Come gas di riempimento si sono usati azoto, argo,
cripto da soli o anche in miscela. Il Kr è il migliore di tali gas perché è abbastanza
inerte chimicamente e ha una bassa conduttività termica, proprietà vantaggiosa per
la limitazione degli scambi termici convettivi.
Il processo di sublimazione del tungsteno col conseguente deposito dello stesso
sulla superficie dell'ampolla è la causa che limita la durata di funzionamento (vita)
delle lampade a incandescenza. Man mano che il processo si svolge, vanno diminuendo la trasparenza dell'ampolla e il flusso luminoso emesso; contemporaneamente il filamento, perdendo materia, si indebolisce e alla fine si rompe.
Un mezzo usato per aumentare la temperatura di colore delle lampade a incandescenza è quello di
colorare di azzurro il vetro dell'ampolla. In questo modo si ottiene una luce meno rossastra e più gradevole per alcune applicazioni. Questo scopo, però, è raggiunto a spese del flusso luminoso emesso,
di cui una parte viene assorbita dal vetro colorato, e del rendimento luminoso, che diminuisce di conseguenza.
Caratteristiche tipiche delle lampade a incandescenza
durata
media
h
temperatura
di colore
K
ΦV
ηV
lm
lm/W
Filamento di carbone
100-1200
3,5
600
2070
Filamento di W nel vuoto
100-600
8
1000
1750
200-30 000
10-20
1000-1500
2850
1000-250 000
20-30
-
3200
Tipo di lampada
Filamento di W in gas inerte
A ciclo di alogeni
Un notevole progresso è stato raggiunto con la lampada a ciclo di alogeni. Essa è
ancora costituita essenzialmente da un filamento di tungsteno che viene reso incandescente per mezzo di una corrente elettrica, ma nell'ampolla è introdotta una piccola quantità di iodio o di altri elementi alogeni. La temperatura del filamento è
elevatissima (≈3000°C); l'ampolla è molto piccola ed è costituita da vetro di quar-
28
APPUNTI DI FISICA TECNICA: FOTOMETRIA
zo; la sua temperatura durante il funzionamento (≈700°C), alquanto più bassa di
quella del filamento, è tuttavia piuttosto alta al confronto con le lampade a incandescenza ordinarie. Nella zona della lampada a più bassa temperatura i vapori di
tungsteno che si liberano dal filamento si combinano chimicamente con lo iodio
presente, formando ioduro di tungsteno WI2 gassoso (o altri composti analoghi).
Questo, migrando verso la zona del filamento caldo, si scompone nei suoi elementi,
dando luogo alla formazione di W metallico che si deposita nuovamente sul filamento. Così si stabi lisce un ciclo del metallo che prolunga la vita del filamento
della lampada; inoltre la parete dell'ampollina si mantiene trasparente perché è evitata l'accumulazione di depositi metallici su di essa.
Nel quadro sono presentati
in sintesi dei dati indicativi Prestazioni delle lampade a incandescenza al variare delle
condizioni dell'alimentazione elettrica
sulle principali caratteri(rapporti delle grandezze ai corrispondenti valori nominali)
stiche delle lampade a incandescenza. Per durata
V/Vn
i/in
W/Wn
d/dn
Φ V/Φ Vn
ηV/ηVn
media delle lampade di un
0,50
0,67
0,33
0,08
0,25
certo tipo si intende il tem0,90
0,94
0,84
0,67
0,79
4,70
po di funzionamento, ge1,00
1,00
1,00
1,00
1,00
1,00
neralmente espresso in ore,
1,10
1,05
1,16
1,40
1,21
0,28
dopo il quale, di un insie1,50
1,27
1,91
4,60
2,40
me abbastanza numeroso
di lampade di quel tipo,
solo il 50% rimane in funzione. Nella tabella non è presente alcun dato per il caso della lampade a ciclo di
alogeni, poiché la durata media di tali lampade varia molto a seconda delle applicazioni. Per le lampade da proiezione cinematografica essa è di ≈2000 h; per riprese
fotografiche di ≈15 h; per riprese cinematografiche e televisive è di 75 h o più.
Le lampade a incandescenza possono essere connesse alla rete di alimentazione
elettrica in serie o in parallelo. Secondo il caso, la variabile imposta sarà quindi rispettivamente la corrente o la tensione. Di norma ogni lampada porta l'indicazione
delle condizioni normali di funzionamento, che sono quelle considerate migliori dal
costruttore dai punti di vista della durata e del rendimento. Al variare delle condizioni di funzionamento reali variano conseguentemente anche le prestazioni della
lampada.
Lo specchietto illustra il modo di variare delle prestazioni delle lampade a incandescenza ordinarie (a filamento di tungsteno in gas inerte) al variare della tensione di
rete o, nel caso di alimentazione in serie, al variare della corrente. Tutti i dati sono
presentati in forma adimensionale, come rapporti delle grandezze ai rispettivi valori
nominali. Questi ultimi sono indicati con l'indice n. Col simbolo d è indicata la durata media delle lampade.
Per quanto detto prima, man mano che le lampade invecchiano, il bulbo si va annerendo, cosicché il flusso luminoso va diminuendo. A ciò spesso si aggiunge l'effetto
3. SORGENTI DI LUCE
29
della polvere che si va depositando sulla superficie esterna dell'ampolla, facendone
crescere il coefficiente di assorbimento.
3.3. Lampade a scarica
3.3.1. La scarica nei gas
I gas, che ordinariamente hanno una bassissima conduttività elettrica, diventano
conduttori quando sono ionizzati, cioè quando in essi sono presenti elettroni liberi
e molecole dotate di carica elettrica per avere perduto uno o più elettroni.
La teoria cinetica dei gas stabilisce che una singola molecola di un gas monoatomico possiede in media una energia cinetica pari a:
3
Ecin . = kT
(1)
2
con k = 1,38 × 10-23 J/K (costante di Boltzmann). Alla temperatura ordinaria tale
energia media è di circa 10-20 − 10-21 J; dello stesso ordine di grandezza sono gli
scambi di energia tra le molecole causati dalle collisioni tra le stesse. L'energia
scambiata nell'urto risulta allora inferiore all'energia necessaria per strappare un
elettrone dall'atomo (energia di ionizzazione), che va da 1 eV a 1 keV (1,6 × 10-19 −
1,6 × 10-16 J). Perciò alla temperatura ordinaria gli scambi di energia che avvengono
tra le molecole in conseguenza delle loro collisioni non bastano a provocare la ionizzazione del gas in misura notevole. Se si innalza la temperatura del gas o si fa
agire su di esso una radiazione corpuscolare o elettromagnetica di sufficiente energia ovvero si accelerano le particelle cariche presenti con un adatto campo elettrico, si creano le condizioni per la ionizzazione del gas e i conseguenti fenomeni,
che sono a fondamento del funzionamento di una lampada a scarica.
Generalmente una lampada a scarica è costituita da un tubo contenente un adatto
gas a una certa pressione; alle due estremità sono posti gli elettrodi, tra i quali viene
stabilita una differenza di potenziale; ne consegue il passaggio di una corrente elettrica attraverso il gas. Nella figura è presentato l'andamento della tensione tra gli
elettrodi in funzione della corrente. Nel primo tratto si osserva un andamento della
i crescente con la V: si tratta del movimento dei pochi ioni ed elettroni liberi sempre presenti nel gas, che sotto l'azione del campo elettrico si dirigono verso gli elettrodi. All'aumentare della tensione le particelle cariche raggiungono, nel percorso
tra un urto e il successivo, velocità sempre maggiori. In conseguenza aumenta l'entità degli scambi energetici causati dalle collisioni tra le particelle; aumenta anche la
probabilità che una collisione determini la ionizzazione di una molecola. Dopo un
tratto della curva (i, V) del tubo a scarica, nel quale la corrente aumenta molto poco all'aumentare della tensione, si produce, per un valore di V che è detto tensione
d'innesco, una densità tanto grande di particelle cariche che il gas diventa un buon
conduttore. Nella curva caratteristica del tubo questo si traduce in un rapido aumento della corrente all'aumentare della tensione. Segue un tratto – quello corrispondente al funzionamento della lampada a scarica – in cui la caduta di potenziale
30
APPUNTI DI FISICA TECNICA: FOTOMETRIA
tra gli elettrodi decresce all'aumentare della corrente; c'è poi un altro tratto, corrispondente alla scarica disruptiva o arco, che interessa il campo delle lampade ad
arco, usate per certe speciali applicazioni.
L'andamento della curva (tensione d'innesco, tensione d'arco, etc.) dipende dalla
forma degli elettrodi e del tubo e dalla
natura del gas; dipende inoltre dal prodotto della pressione del gas per una distanza caratteristica, come può essere la
distanza tra gli elettrodi (legge di Pa- Schema di una lampada a scarica. A dx
schen). L'aumento della pressione del gas, curva caratteristica di funzionamento.
abbreviando il percorso libero medio delle
particelle, ha un effetto simile a quello dell'aumento delle dimensioni del tubo, cioè,
a pari tensione applicata, della diminuzione del campo elettrico nel gas. Riducendo
la pressione (o le dimensioni), si produce l'effetto di un abbassamento della tensione d'innesco.
Il particolare andamento discendente della curva caratteristica rende instabile il funzionamento del tubo. Per chiarire meglio ciò, si consideri che qualunque elemento
di circuito, la cui caratteristica V = V(i) abbia in un tratto la pendenza negativa, è
instabile nello stesso tratto. Sia, in un
certo istante, P il punto di funzionamento dell'elemento L del circuito
della figura, alimentato alla tensione
costante VA; R rappresenta la resistenza del circuito di alimentazione, che
supponiamo di piccolo valore. Un'eventuale piccola variazione in meno
della corrente che passa in L determina
La lampada a scarica col suo circuito d'aliun aumento della caduta di potenziale mentazione. A dx la curva caratteristica (i, V).
attraverso l'elemento stesso L (punto
Q). Ai capi della resistenza R viene così a diminuire la dif ferenza di potenziale applicata; ciò determina una diminuzione
ulteriore della corrente che attraversa il circuito. Sulla caratteristica di L, allora, il
punto di funzionamento si sposterà ancora verso le i decrescenti, e così via. Il circuito potrà stabilizzarsi quando il punto di funzionamento si sposterà oltre il punto
M. Una analoga instabilità si riconosce se si immagina una piccola variazione iniziale in aumento della corrente a partire dal punto P.
Per rimediare a tale instabilità si inserisce nel circuito una resistenza aggiuntiva (resistenza zavorra), in modo che il valore R della resistenza posta in serie a L non
sia trascurabile: la caduta di potenziale ai capi di L e quella ai capi di R, sommate,
bilanciano in ogni istante la tensione di alimentazione VA. La caratteristica di R essendo una retta di pendenza pari alla resistenza, la caratteristica dell'insieme di L ed
3. SORGENTI DI LUCE
31
R in serie sarà la curva, indicata con c' nella figura, che non ha più tratti con pendenza negativa e quindi instabili. Perché questo risultato sia raggiunto è necessario
che la resistenza posta complessivamente in serie a L sia maggiore del valore assoluto della pendenza della caratteristica di L nel tratto che interessa per il funzionamento:
dV
.
(2)
d i max .
Con lo zavorramento il punto P diventa un
punto di funzionamento stabile; d'altra parte la
tensione di cui si deve disporre è ora un po'
maggiore, dovendosi bilanciare anche la caduta sulla resistenza zavorra.
Se, come solitamente accade, si alimenta con
tensione alternata, per limitare le perdite di
potenza per effetto Joule si può inserire, in
luogo del resistore R, un reattore, che di solito
è di tipo induttivo.
Se la lampada è alimentata con una tensione Caratteristiche di funzionamento del
alternata, il suo funzionamento comprende una circuito d'alimentazione senza (c) e
successione di fasi di spegnimento e di riac- con (c') la resistenza zavorra.
censione della scarica, con frequenza pari al doppio della frequenza di rete: a ogni
semiperiodo della tensione di alimentazione corrisponde un ciclo di accensione
della scarica; la corrente scorre alternativamente nell'uno e nell'altro verso. Infatti,
quando la tensione applicata alla lampada
scende dal suo massimo verso lo zero, a un
certo punto la scarica si estingue, per riaccendersi al risalire della tensione durante il
successivo semiperiodo. La riaccensione del
tubo è facilitata dal fatto che, benché non vi
sia più la scarica autonoma, il gas è ancora ionizzato per effetto della precedente fase; una
volta che la scarica riparte, corrente e tensione
tendono a stabilizzarsi per un breve intervallo
di tempo prima del seguente spegnimento. In Dispositivi d'avviamento per la lampada a scarica.
ogni istante la corrente è tale che la somma
della caduta di potenziale tra gli elettrodi e di
quella che si ha all'impedenza zavorra uguaglia il valore istantaneo della tensione di
alimentazione. L'andamento nel tempo della corrente risulta complicato: la forma
d'onda è molto diversa dalla sinusoide della tensione di alimentazione ed è anche
notevolmente sfasata in ritardo sulla tensione. La lampada si comporta, in questo,
come un'induttanza con un fattore di potenza piuttosto basso (≈0,5). Negli impianti
di illuminazione comprendenti molte lampade a scarica, con grande potenza comR>
32
APPUNTI DI FISICA TECNICA: FOTOMETRIA
plessivamente installata, spesso è necessario procedere al rifasamento, che si fa generalmente per mezzo di condensatori.
Si è accennato al fatto che la riaccensione della lampada, che avviene a ogni semiperiodo, è facilitata dal fatto che il gas contenuto nel tubo è già ionizzato dalla precedente scarica. All'avviamento, quando tale ionizzazione manca, è necessario
adottare particolari mezzi per provocare il primo innesco. Nelle figure sono presentati due diversi dispositivi, dei molti utilizzabili. Il primo comprende un elettrodo ausiliario C, connesso elettricamente con l'elettrodo A attraverso una resistenza
R e collocato in vicinanza dell'elettrodo B. A freddo, quando il gas non è ionizzato
e quindi non è un buon conduttore, la corrente passa tra B e C iniziando la ionizzazione del gas nella zona più vicina all'elettrodo B; quando questa è sufficientemente estesa a tutto il tubo e in questo la scarica si è innescata, la resistenza del
percorso nel gas diventa piccola al confronto con quella del tratto C-R-A; la corrente passa tutta nel gas e l'elettrodo C diventa praticamente inattivo.
Col secondo sistema il dispositivo di avviamento S (starter) è costituito da un interruttore che può chiudere o aprire il ramo di circuito che collega i due elettrodi
della lampada. Questi sono costituiti a loro volta da tratti di conduttori elettrici
che, quando S sia chiuso, risultano posti in serie. All'avviamento il contatto è chiuso; quando si alimenta la lampada, i due elettrodi sono percorsi da corrente e si
scaldano per effetto Joule. Durante questo tempo gli elettrodi emettono elettroni liberi per l'effetto termoelettronico (effetto Richardson - Fermi). Dopo un po' di
tempo il contatto si apre automaticamente e l'intera differenza di potenziale viene a
stabilirsi tra gli elettrodi; nel gas, già ionizzato, si avvia la scarica.
Tra gli interruttori automatici di avviamento, il più comunemente usato è quello
costituito da una minuscola lampada a scarica in gas raro, di cui uno dei due elettrodi è costituito da una lamina bimetallica. A freddo i due elettrodi sono separati
da una piccola distanza; quando si stabilisce la tensione tra
gli elettrodi la scarica che avviene nel gas fa salire la temperatura, sicché i due elettrodi dello starter vengono a
toccarsi chiudendo il contatto. Gli elettrodi della lampada
cominciano allora a essere percorsi dalla corrente e si scaldano; nel gas contenuto nella lampada si crea così la ionizzazione necessaria per predisporre la lampada all'innesco. Il piccolo tubo a scarica dello starter, non più
sede di scarica nel gas, comincia a raffreddarsi, finché gli
elettrodi tornano a staccarsi. A questo punto tra gli elet- Starter con lampada a
trodi della lampada viene ad applicarsi l'intera tensione di scarica.
alimentazione e la lampada si accende. Durante il funzionamento della lampada la tensione ai capi del piccolo tubo a scarica dello starter
non è più sufficiente per l'innesco e la piccola corrente che attraversa lo starter è di
entità trascurabile. Se, invece, il processo di accensione della lampada dovesse fallire, il ciclo di avviamento ricomincerà in modo automatico.
3. SORGENTI DI LUCE
33
3.3.2. Lampade a vapori di mercurio
Utilizzano la scarica elettrica nel mercurio allo stato aeriforme. Questo ha solitamente uno spettro di emissione costituito principalmente da un paio di righe situate
nel campo della radiazione ultravioletta (254 nm e 185 nm), quindi non utili per la
visione. Ad alta pressione si manifestano anche altre righe nel campo delle radiazioni visibili (blu, verde); con l'ulteriore aumento della pressione le righe si vanno allargando in bande e lo spettro di emissione diviene del tipo continuo, pur se
mancante delle lunghezze d'onda corrispondenti al rosso.
Caratteristiche di alcuni tripi di sorgenti luminose
Dati rappresentativi di valori dichiarati da alcuni fabbricanti di lampade
(lm)
(lm/W)
Temperatura
di colore
(K)
Lampada a incandescenza a bulbo trasparente
W = 60W; V = 220 V
730
12
2800
1000
Lampada a incandescenza a bulbo trasparente
W = 150W; V = 220 V
2220
15
2800
1000
Lampada a incandescenza ad alogeni
W = 150W; V = 220 V
2500
17
3000
2000
Lampada fluorescente tubolare; L = 590 mm;
W = 18 W
1450
81
4000
5000
Lampada fluorescente tubolare; L = 1500 mm;
W = 58 W
5400
93
4000
5000
Lampada fluorescente compatta; zoccolo a vite;
W = 18 W
900
50
2700
5000
Lampada a vapori di mercurio ad alta pressione
W = 50 W
1600
32
2900
9000
Lampada a vapori di sodio ad alta pressione
W = 100 W
9500
95
-
9000
Lampada ad alogenuri metallici; W = 75 W
5000
67
3000
6000
Tipo di lampada
ΦV
ηV
Durata
(h)
Le lampade a vapori di mercurio a bassa pressione, per quanto detto sopra, non
vengono usate per illuminazione ma per particolari operazioni tecnologiche che richiedono l'uso delle radiazioni UV. Quelle ad alta pressione sono piuttosto interessanti, particolarmente per il rendimento luminoso, che va da 30 a 50 lm/W, considerando anche le perdite nel dispositivo alimentatore-stabilizzatore-rifasatore.
Queste lampade sono costituite da un'ampolla di vetro trasparente che racchiude,
oltre al piccolo tubo dove avviene la scarica, il resistore di avviamento. Il tubo di
scarica è di vetro di quarzo, abbastanza robusto da resistere alle alte temperature e
alle alte pressioni (fino a ≈25 bar) che il vapore di mercurio raggiunge durante il
34
APPUNTI DI FISICA TECNICA: FOTOMETRIA
funzionamento. Il circuito di alimentazione comprende un induttore per la stabilizzazione e un condensatore per il rifasamento.
Una caratteristica di queste lampade è che esse non possono essere subito riavviate
dopo lo spegnimento. Infatti, se viene a mancare la ionizzazione del vapore di mercurio a caldo, quando la pressione del vapore è alta, la tensione che si applica agli
elettrodi non è sufficiente per l'innesco: allora si deve attendere qualche minuto affinché la temperatura si abbassi, la pressione di conseguenza si abbassi anch'essa e
la scarica possa di nuovo innescarsi con la tensione a disposizione (v. legge di Paschen, § 3.3.1).
In alcuni tipi di lampade a vapori di mercurio sono aggiunti degli ioduri di Na, In,
etc. per correggere le caratteristiche dello spettro di emissione e migliorare il rendimento luminoso, che così può arrivare fino a 95 lm/W.
Allo stesso scopo vengono prodotte delle lampade a vapori di mercurio, la cui ampolla esterna è internamente rivestita di speciali sostanze (fosfòri) capaci di convertire la radiazione UV in radiazione visibile, secondo il metodo impiegato per le
lampade fluorescenti (v. § 3.4).
3.3.3. Lampade a vapori di sodio
In queste si utilizza la proprietà del vapore di sodio di emettere alla lunghezza d'onda di 589 nm, che è vicina alla lunghezza d'onda di massima visibilità.
Poiché il sodio alla temperatura ordinaria è solido, all'avviamento è necessario che
il metallo passi allo stato aeriforme prima che possa emettere. Ciò si ottiene introducendo nel tubo di scarica del neo, nel quale all'inizio avviene la scarica. Dopo
qualche minuto, quando la temperatura si innalza abbastanza e il sodio passa allo
stato di vapore, esso partecipa all'emissione con la sua caratteristica luce gialla. Il
tubo della scarica è racchiuso entro un involucro tubolare di protezione. Per limitare le dispersioni di calore, tra i due tubi è praticato il vuoto.
La caratteristica più notevole di queste lampade è che esse emettono una luce gialla
quasi perfettamente monocromatica (si tratta di due righe molto vicine, a λ =
589 nm e λ = 589,6 nm, dalle colorazioni praticamente non distinguibili). Questa
caratteristica rende tali lampade inutilizzabili per l'illuminazione di ambienti interni
di soggiorno e per tutte le applicazioni nelle quali è importante la distinzione dei
colori. Le lampade al sodio possono essere usate invece per l'illuminazione di nodi
ferroviari, autostrade etc.
Se si fa crescere la pressione dei vapori di sodio nel tubo di scarica, si ottiene uno
spettro di emissione non più a righe ma a bande o continuo, che dà una sensazione
cromatica più accettabile mentre, contemporaneamente, il rendimento luminoso si
abbassa. La temperatura del tubo di scarica deve essere più alta che nel tubo a bassa pressione: il tubo è realizzato con uno speciale materiale ceramico trasparente e
resistente alla pressione, all'alta temperatura e all'azione chimica del sodio.
3. SORGENTI DI LUCE
35
3.3.4. Lampade allo xeno
La scarica elettrica ad arco in atmosfera di xeno consente di ottenere spettri di
emissione che riproducono con buona approssimazione, nel campo della luce visibile, quello della radiazione solare. Ne consegue una resa dei colori fedele, cosicché le lampade allo xeno sono ben impiegabili per l'illuminazione degli ambienti interni ed esterni urbani e anche per proiezioni e riprese fotografiche e cinematografiche.
Le lampade sono costituite da un tubo di quarzo contenente il gas e gli elettrodi.
Le temperature raggiunte nel gas ionizzato sono molto alte e bisogna prendere adatte precauzioni per proteggere l'involucro di quarzo dall'eccessivo riscaldamento.
A questo scopo le lampade di maggiore potenza sono completate da un sistema di
raffreddamento ad acqua.
Alcuni tipi richiedono l'alimentazione in corrente continua; tutti richiedono un dispositivo (accenditore) che all'avviamento applica tra i due elettrodi una elevata
tensione alternata di alta frequenza che inizia la ionizzazione del gas e innesca l'arco.
3.3.5. Tubi ad alta tensione
Sono tubi molto sottili e lunghi, usati soprattutto per insegne e decorazioni. Possono essere riempiti di varii gas, a seconda del colore della luce che si vuole ottenere. Vanno alimentati con tensione alternata, di valore proporzionale alla lunghezza del tubo (≈400 V/m). Anche in queste lampade il colore della luce emessa
dal gas può essere modificato con l'uso di sostanze fluorescenti applicate sulla superficie interna del tubo. Il rendimento luminoso di queste sorgenti è modesto
(<10 lm/W).
3.4. Lampade fluorescenti
3.4.1. La fluorescenza
Alcune sostanze hanno la proprietà di assorbire le radiazioni elettromagnetiche di
piccola lunghezza d'onda e di riemettere l'energia relativa sotto forma di radiazioni
di lunghezza d'onda maggiore. Il fenomeno è detto fluorescenza; l'emissione cessa
entro un tempo molto breve (≈10-8 s) dalla cessazione della radiazione eccitatrice.
Un fenomeno simile e spesso coesistente con la fluorescenza è quello della luminescenza o fosforescenza, che invece si prolunga di più nel tempo.
Nella tecnica dell'illuminazione si utilizza la fluorescenza di alcune sostanze, dette
fosfòri, generalmente costituiti da tungstati, fosfati, silicati, etc. di Ca, Mg, Zn.
Queste sostanze sono sensibili all'eccitazione da radiazioni UV e sono impiegate
nei tubi a scarica in vapori di Hg, le cui principali lunghezze d'onda di emissione nel
funzionamento a bassa pressione sono di ≈254 nm e ≈185 nm. I fosfori, colpiti
36
APPUNTI DI FISICA TECNICA: FOTOMETRIA
dalla radiazione UV del mercurio, la assorbono e successivamente la riemettono
con una lunghezza d'onda compresa nel campo della radiazione visibile.
Il colore della luce risultante varia con la natura dei fosfori e anche secondo la natura di particolari sostanze (attivatori) disperse in tracce nei sali fluorescenti. L'effetto risultante è la trasformazione in luce della radiazione UV emessa dal mercurio. Il rendimento luminoso delle lampade fluorescenti risulta generalmente molto
elevato (70 – 80 lm/W).
3.4.2. Lampade fluorescenti tubolari
Generalmente i tubi sono riempiti di argo e vi è aggiunta una piccola quantità di
mercurio. La presenza dell'argo ha lo scopo di facilitare l'innesco della scarica all'accensione.
Il colore della luce emessa, come detto, dipende dalle sostanze di cui è rivestito
internamente il tubo. Si va dalla luce bianco-azzurra (temperatura di colore
≈6500 K) sino alla luce di colore bianco-caldo (temperatura di colore ≈3000 K),
che più si avvicina alla luce emessa dalle lampade a incandescenza ed è più gradevole nell'uso negli ambienti interni.
Caratteristica comune delle lampade tubolari è la bassa luminanza della superficie
emittente (4000 – 7000 cd/m2). Tale caratteristica talvolta rende possibile l'uso di
queste sorgenti senza che sia necessario schermarle alla vista diretta per evitare
l'abbagliamento, come invece si deve fare con lampade di altro tipo.
Ordinariamente l'alimentazione di questa lampade è fatta attraverso un induttore
che serve da stabilizzatore; è presente anche un dispositivo di avviamento che funziona con la ionizzazione del gas per effetto termoelettronico. Vi sono però dei tipi
di lampade fluorescenti e anche dei particolari reattori che eliminano la necessità di
un separato avviatore, creando in varii modi una sovrattensione tra gli elettrodi all'avviamento. Generalmente con tali sistemi si ottiene un'accensione istantanea della
lampada, ma si ha una certa dissipazione di energia elettrica, superiore a quella che
si verifica nel sistema con reattore e starter.
3.4.3. Lampade fluorescenti a bulbo
Simili nel principio di funzionamento alle lampade tubolari, se ne distinguono perché l'emissione primaria avviene in un tubo a vapori di mercurio ad alta pressione
che, come visto, ha uno spettro d'emissione continuo o a bande, ma contiene molta
radiazione UV e quasi niente rosso. La conversione della radiazione UV in radiazione visibile è compiuta anche qui da adatte sostanze che ricoprono la superficie
interna del bulbo. Lo spettro d'emissione risultante è ancora fortemente discontinuo, ma comprende delle bande ben disperse in tutto lo spettro visibile, cosicché
l'effetto cromatico è accettabile. Il rendimento luminoso è alto, da 40 a 60 lm/W,
considerando anche le perdite nell'alimentatore.
3. SORGENTI DI LUCE
37
3.4.4. Lampade a luce miscelata
Sono simili alle lampade fluorescenti a bulbo viste al precedente § 3.4.3, ma all'interno del bulbo è aggiunto un filamento di tungsteno collegato in serie al tubo a
scarica, che, emettendo per incandescenza col suo spettro continuo ricco di radiazioni di grande lunghezza d'onda, dà un utile contributo alla produzione di flusso
luminoso e migliora la resa dei colori. Il filamento stesso fa da resistenza zavorra,
cosicché per queste lampade non c'è bisogno di un reattore stabilizzatore. Valori
del rendimento luminoso intermedii tra quelli delle lampade fluorescenti e delle
lampade a incandescenza.
3.5. Lampade a combustione
Sul fenomeno dell'emissione luminosa prodotta dalla combustione si basarono tutte
le sorgenti artificiali di luce usate in passato, finché non entrarono in uso le lampade elettriche a filamento incandescente (T. A. Edison, 1879). Sulla combustione
si fonda il funzionamento delle torce, delle lucerne a olio, delle candele, delle lampade a gas e ad acetilene. In esse si utilizza direttamente la luminosità dei gas caldi
costituenti la fiamma, ma soprattutto la luminosità delle particelle solide incandescenti presenti nella fiamma: queste hanno un'emissione termica vicina a quella al
corpo nero di pari temperatura e spesso possono essere assimilate, per questo riguardo, a corpi grigi.
Le sorgenti a combustione hanno la caratteristica di avere un rendimento luminoso
molto basso poiché una gran parte dell'energia chimica spesa si perde con l'allontanamento dei fumi caldi, col riscaldamento convettivo dell'aria circostante e anche
per incompleta combustione: insomma, solo una piccola parte dell'energia spesa si
traduce in un'emissione di energia radiante. Oltre a ciò, poiché la temperatura dei
corpi emittenti non è mai molto alta, la massima parte dell'energia irradiata è costituita da radiazioni non visibili (cfr. legge di Planck, legge di Wien) ed è perduta
nei riguardi dello scopo per il quale è usata la sorgente.
Per migliorare la composizione spettrale dell'energia irradiata si può usare la reticella Auer (1885), dispositivo che ha dato ottimi risultati nelle lampade a gas illuminante, a petrolio, a propano, etc. È una reticella di cotone che viene posta intorno alla fiamma, così da por tarsi ad alta temperatura e carbonizzare. Essa è impregnata di una adatta miscela di sostanze (ossidi di torio e di cerio) che ha una emissività integrale molto bassa, ma una alta emissività spettrale nel campo della radiazione visibile. Per data temperatura la reticella ha perciò un'emittanza integrale minore di quella del corpo nero; ciò fa sì che, dovendo l'e nergia emessa sempre bilanciare a regime l'energia assorbita, la temperatura di equilibrio della reticella sale
rispetto a quella che un corpo nero raggiungerebbe. Quanto all'energia irradiata
(∝ ∆[T 4]), questa, specialmente nel campo della radiazione visibile, aumenta ri-
38
APPUNTI DI FISICA TECNICA: FOTOMETRIA
spetto a quella dispersa per convezione (∝ ∆T). Con l'aumento della temperatura si
ottiene anche un aumento della temperatura di colore della luce emessa.
Attualmente l'interesse per le sorgenti di luce a combustione è limitato ad alcune
sorgenti portatili e a pochi altri casi. Per il resto tali sorgenti sono cadute in disuso
a causa della grande comodità d'uso e dell'ottimo rendimento che sono proprii delle
sorgenti elettriche.
39
4. ILLUMINAZIONE DEGLI AMBIENTI CHIUSI
4.1. Requisiti dell'impianto di illuminazione
4.1.1. Illuminamento
La prima condizione che un impianto di illuminazione deve soddisfare è che sulle
superficie da osservare venga realizzato un illuminamento medio sufficiente per
una visione abbastanza chiara in relazione all'attività da svolgere. In particolare si
prende in considerazione l'illuminamento della zona di lavoro (spesso è un piano di
lavoro), cioè della regione dello spazio verso la quale l'operatore rivolge lo sguardo per osservare gli oggetti, gli strumenti o le carte con cui svolge la sua attività.
Si è trovato che il valore soddisfacente dell'illuminamento me- Ampiezze angolari dei minimi particolari da distindio nella zona di lavoro dipende guere nel compiere alcune attività.
Lavoro d'orologeria
1'
dalle dimensioni angolari degli
Disegno
tecnico
1'
20"
oggetti o dei loro particolari miRicamo a mano
1' 50"
nimi che devono essere distinti
dall'operatore durante l'attività.
Montaggio di pezzi meccanici
2' 20"
Qualche esempio di valori tipici
Lavorazione di grossi pezzi meccanici
3'
di tali dimensioni angolari è dato
Lavorazioni di nessuna precisione
4'
nel riquadro.
Una semplice espressione dell'illuminamento minimo sul piano di lavoro, raccomandata dalla IES (Illuminating Engineering Society) inglese, è la seguente:
2 × 105
lx
(1)
rα1,5
dove r è l'albedo degli oggetti osservati, espressa in percentuale, e α è l'angolo sotto il quale sono visti
i particolari più pic- Valori di illuminamento in lux secondo la grandezza dei particocoli, espresso in mi- lari da osservare e il contrasto (AFE)
dimensioni dei
contrasto
contrasto
nuti.
contrasto alto
particolari
medio
basso
Per una indicazione
piccolissimi
2000–3000
5000–10 000 20 000–40 000
più accurata si deve
piccoli
400–800
1200–3500
4000–8000
tenere conto anche
medii
80–200
300–600
900–2000
del contrasto di lugrandi
40–90
100–250
500–900
minanza tra l'oggetto
da osservare e lo
sfondo. A questo proposito è opportuno ricordare che l'illuminamento misura la luce che incide su un dato oggetto, mentre lo stimolo che l'occhio riceve dipende
dall'illuminamento di quella parte della rètina sulla quale si forma l'immagine dell'oggetto; questo dipende dalla luminanza dell'oggetto stesso. La capacità dell'occhio di distinguere gli oggetti è legata al contrasto di luminanza tra gli oggetti stessi e lo sfondo. Il contrasto C può essere definito come:
EV =
40
APPUNTI DI FISICA TECNICA: FOTOMETRIA
L′ − L′′
Valori tipici di illuminamento in locali di diver(2)
L′′
se destinazioni
con L' e L" rispettivamente la magluci di sicurezza nei locali pubblici
5 lx
giore e la minore delle due luminan(impianto a batteria)
ze. Se l'oggetto osservato e lo
autorimesse
70 lx
sfondo sono entrambi diffondenti e
cinema e teatri (sale)
100 lx
sottoposti allo stesso illuminamenilluminamento minimo per qualsiasi la150 lx
to, le loro luminanze sono proporvoro
zionali ai rispettivi coefficienti di riattività industriale non di precisione
200 lx
flessione. Così un grande contrasto
attività industriale di precisione, uffici
300 lx
amministrativi, scuole
si avrà nella lettura di caratteri
stampati in nero su carta bianca, un
uffici tecnici, laboratori
750 lx
contrasto minore nella lettura di un
attività di grande precisione
1 klx
testo scritto a matita, un contrasto
ancora più piccolo nel caso di ricamo da eseguire su una stoffa di un certo colore con filo di colore simile, specialmente se tale colore è scuro. L'esperienza mostra che, a parità di altre condizioni, quando il contrasto tra gli oggetti osservati e lo sfondo è piccolo, è grande il valore dell'illuminamento da realizzare nel campo di lavoro per ottenere una sufficiente visibilità e condizioni di lavoro non penose.
Il valore dell'illuminamento da considerare sufficiente per eseguire un certo còmpito dipende perciò, sia dalle dimensioni angolari dei particolari che devono essere
distinti, sia dal loro contrasto di luminanza con lo sfondo. I valori di illuminamento
minimi per diverse combinazioni di dimensione degli oggetti e di contrasto di luminanza vengono proposti dagli appositi organismi normatori e talvolta adottati dagli
stati come norme ufficiali. Come esempio di tali regole si presentano qui nel quadro alcuni valori di illuminamento in lux raccomandati in Francia dall'Association
Française de l'Éclairage (AFE) per contrasto di luminanza alto, medio, basso.
Alcuni enti normatori come quello inglese IES e quello tedesco Deutscher Industrie Normenausschuss (DIN) indicano, oltre all'illuminamento minimo, anche
quello ottimo, tenendo conto dell'inopportunità che l'illuminamento sia troppo
grande. Infatti, se da un lato un elevato valore di EV migliora la visibilità degli oggetti e la produttività del lavoro, dall'altra può causare una certa stanchezza visiva e
mentale che, se il lavoro è protratto nel tempo, porta a un decadimento della qualità del lavoro e del benessere del lavoratore.
In Italia delle norme sui valori di illuminamento sono contenute in vari regolamenti
di costruzione ed esercizio degli edifici civili e industriali; in prima approssimazione
o in mancanza di dati precisi la tabella nel quadro può dare qualche idea sull'illuminamento da realizzare in alcune condizioni.
C=
4. ILLUMINAZIONE DEGLI AMBIENTI CHIUSI
41
4.1.2. Illuminazione localizzata
Si è visto come il contrasto di luminanza tra l'oggetto da osservare e lo sfondo è
utile per una visione chiara dei particolari. A questo scopo è utile pure la presenza
di ombre: esse arricchiscono l'osservatore di informazioni sulle dimensioni e sulla
forma dei corpi e rendono più agevole il riconoscimento e la localizzazione di questi. Per questo motivo per le operazioni di montaggio di pezzi meccanici, ricamo e
cucito, disegno tecnico etc. spesso è utile illuminare tutto l'ambiente con un illuminamento relativamente basso con sistemi di illuminazione diffusa, limitando al
solo posto di lavoro l'elevato illuminamento necessario, che si ottiene con un apparecchio illuminante aggiuntivo posto vicino all'operatore.
Tale modo può risultare conveniente anche economicamente, poiché evita la spesa
necessaria per ottenere alti illuminamenti in tutto l'ambiente, anche là dove questi
non sono necessari. D'altra parte questa pratica, che migliora la visibilità al posto di
lavoro, può dar luogo agli inconvenienti cui si accenna al paragrafo seguente.
4.1.3. Abbagliamento
Se la luminanza del campo di lavoro è molto più alta della luminanza del resto dell'ambiente (pareti, pavimento e quanto altro entra nel campo visivo dell'operatore),
può verificarsi un affaticamento dell'operatore quando tale situazione duri molto
nel tempo.
Il caso più semplice è quello di una sorgente di luce che sia direttamente visibile
dall'osservatore durante il suo lavoro. Si parla allora di abbagliamento diretto. Per
evitarlo si cerca di schermare adeguatamente le lampade, cosicché la luce raggiunga l'operatore dopo riflessione o per trasparenza diffusa. Il problema si pone
soprattutto con le lampade a incandescenza, il cui filamento ha un'alta luminanza; è
meno grave con le lampade a bulbo traslucido e ancora meno con le lampade fluorescenti tubolari, che hanno una bassa luminanza. In ogni modo è bene evitare che
vi siano sorgenti di luce visibili dall'operatore entro un cono di semiapertura ≈30°
intorno al suo asse visivo.
Capita però frequentemente che, mentre la sorgente luminosa non è direttamente
visibile, è visibile il suo riflesso su una superficie speculare o lucida posta vicino all'asse ottico dell'operatore: è il caso dell'abbagliamento indiretto. Questo si verifica
quando si usa una lampada da tavolo su una scrivania lucida, quando lo schermo
convesso di un calcolatore riflette la luce di una finestra o di una sorgente di luce
posta al soffitto e in altri casi analoghi. L'abbagliamento indiretto ha effetti simili a
quelli dell'abbagliamento diretto, ma talvolta la sua eliminazione può essere più difficile.
Simili condizioni di fatica sono prodotte da un eccessivo contrasto di luminanza tra
il piano di lavoro e l'ambiente circostante, quando si effettui l'illuminazione concentrata del posto di lavoro (§ 4.1.2), poiché allora l'operatore, ogni volta che distoglie lo sguardo dal suo lavoro, deve operare un adattamento dell'occhio alle diverse
42
APPUNTI DI FISICA TECNICA: FOTOMETRIA
condizioni di luce. Per evitare questo effetto, in generale meno grave dell'abbagliamento, si dovrebbe limitare il contrasto di luminanza al valore di 2 – 3, equivalente a un rapporto massimo tra le luminanze di 3 – 4.
4.1.4. Colore della luce
Gli stimoli visivi raccolti dall'occhio, e tra questi quelli che danno origine alla sensazione cromatica, sono sottoposti a un processo mentale inconscio di elaborazione. Il prodotto di tale processo psichico, che è detto rappresentazione o anche
fantasma, è il risultato, sia delle informazioni raccolte dall'occhio, sia di altre informazioni contemporaneamente acquisite da altri organi di senso, sia, infine, del
ricordo di percezioni sensorie precedenti.
Tale processo di elaborazione degli stimoli visivi ci permette, tra l'altro, di usare
per l'illuminazione artificiale sorgenti emittenti radiazioni di composizioni spettrali
molto diverse. Se soggiorniamo in un ambiente illuminato da una sorgente la cui
curva dell'emittanza spettrale ε(λ) si discosti da quella della luce solare (p. es. un
fuoco o una lampada a incandescenza), le sensazioni cromatiche raccolte dall'occhio vengono mentalmente modificate (si potrebbe dire che vengono tarate) in
modo tale da compensare la colorazione della sorgente di luce. Perciò entro certi
limiti qualsiasi sorgente, purché non manchi del tutto di grandi porzioni dello spettro visibile, può essere considerata bianca per i normali usi di illuminazione (1).
D'altra parte una sorgente di composizione spettrale simile a quella naturale produce un'illuminazione più riposante e gradevole ed è quindi più conveniente per gli
ambienti dove si debba soggiornare a lungo. Perciò la migliore sorgente di luce
avrà nel campo tra 380 e 780 nm una curva di emittanza spettrale non molto diversa da quella di un corpo nero con una temperatura di colore di circa 5000 –
6000 K.
Ciò vale per grandi valori di illuminamento (oltre ≈500 lux) mentre per bassi valori
di illuminamento risulta più gradevole una temperatura di colore inferiore, cioè una
luce più rossastra.
4.2. Illuminamento prodotto da una sorgente puntiforme
Il calcolo dell'illuminamento in un punto generico del piano di lavoro, quando siano
stabiliti il numero, la natura e la disposizione delle sorgenti di luce (calcolo di verifica), è un passo fondamentale nella pratica della tecnica dell'illuminazione. Il caso
più semplice che può presentarsi è quello di una sola sorgente puntiforme S posta a
distanza r dal generico elemento di area dA, di cui si vuol calcolare l'illuminamento.
1
) Questo stesso processo psichico di correzione dei colori rilevati dall'occhio è la causa del disagio
che si prova quando in uno stesso ambiente sono presenti contemporaneamente sorgenti luminose
aventi temperature di colore molto diverse.
4. ILLUMINAZIONE DEGLI AMBIENTI CHIUSI
43
Detta IV l'intensità luminosa della sorgente nella direzione dell'area dA e detto dΩ
l'angolo solido sotto il quale l'area dA è vista dalla sorgente S, si ha la seguente
espressione dell'illuminamento EV su dA:
d Φ V I V d Ω I V d A cos α I V cos α
EV =
=
=
=
(1)
dA
dA
r2 d A
r2
dove α è l'angolo formato dalla normale alla superficie dA con la retta congiungente dA con la
sorgente S. Se la superficie dA fosse posta perpendicolarmente al raggio uscente da S, si avrebbe
il valore massimo dell'illuminamento:
I
EV = V2 .
(2)
r
Per un'area A di estensione finita, se questa è abbastanza piccola perché IV, α, r possano considerarsi
poco variabili da un punto all'altro di essa, si può Illuminamento prodotto su dA
dalla sorgente S.
porre approssimativamente:
I cos α
EV = V 2 .
(3)
r
dove EV, IV, α, r sono i rispettivi valori medi; in generale invece sarà necessario applicare la (1) punto per punto o, se si vuole
fare il calcolo in modo approssimato, suddividere l'area A in porzioni, per ciascuna
delle quali si ritenga di potere scrivere la
(3) con sufficiente approssimazione.
Nel caso che siano presenti più sorgenti
concentrate, poiché l'illuminamento prodotto in un punto è la somma degli illuminamenti prodotti dalle singole sorgenti, per
ciascuno dei punti considerati si calcola EV
come somma dei termini come (3) corri- A tratto intero: curve di uguale illumispondenti alle singole sorgenti di luce pre- namento su un'area illuminata da due
senti. Questo è un metodo di calcolo utiliz- sorgenti. Linee punteggiate per le singole
sorgenti.
zabile in fase di verifica, cioè quando si sia
stabilita una certa distribuzione di sorgenti
nell'ambiente e si voglia calcolare il conseguente illuminamento in alcuni punti
scelti, ad esempio per verificare l'uniformità dell'illuminamento sul piano di lavoro.
A questo scopo, una volta calcolato il valore di EV in un numero sufficiente di
punti, spesso è utile rappresentare graficamente i risultati tracciando delle curve di
uguale illuminamento (curve isolux), che permettono di farsi visivamente un'idea
degli effetti del dato sistema di sorgenti.
44
APPUNTI DI FISICA TECNICA: FOTOMETRIA
4.3. Illuminamento prodotto da una sorgente estesa
Una sorgente non puntiforme può essere una sorgente lineare, cioè con una dimensione (la lunghezza) molto maggiore delle altre due, o una sorgente estesa almeno
in due direzioni dello spazio. Il calcolo è condotto in modo concettualmente uguale
a quello del § 4.2, considerando la sorgente di luce suddivisa in elementi di lunghezza o di area infinitesima, ciascuno dei quali può essere trattato come una sorgente puntiforme, di cui si conosce la superficie fotometrica di emissione. L'effetto
prodotto dall'intera sorgente luminosa è ottenuto integrando a tutta la lunghezza o
a tutta la superficie della sorgente, secondo il caso.
La sorgente lineare può costituire un buon modello di una lampada fluorescente
tubolare. Poiché il tubo ha la stessa luminanza in tutti i suoi punti e
si comporta come una sorgente
lambertiana, la superficie fotometrica di solito assume forme molto
semplici. D'altra parte, ben di rado
una sorgente è installata senza un
apparecchio illuminante che lo
contenga e ne modifichi il solido
fotometrico d'emissione nel modo
1. Sorgente posta al soffitto; superficie illuminata al
desiderato.
pavimento.
Invece il modello della sorgente
estesa su un piano, lambertiana e di luminanza uniforme, è adeguato a rappresentare le caratteristiche degli apparecchi illuminanti collocati al soffitto, nei quali la luce
delle sorgenti (per lo più tubi fluorescenti) è dispersa da uno schermo di vetro smerigliato o di materiale plastico avente la superficie formata a piccole bugne o diversamente lavorata in modo che risulti diffondente. Apparecchi illuminanti di questo
tipo sono molto comuni nei locali chiusi diversi dalle abitazioni, dove è una buona
caratteristica la loro bassa luminanza: delle grandi porzioni della superficie del soffitto costituiscono esse stesse le sorgenti di luce; talvolta l'intero soffitto è reso luminoso in questo modo.
Per il calcolo dell'illuminamento in un punto (per esempio, un punto del piano di
lavoro) vale ancora la (1) del § 4.2, però espressa in forma infinitesima con riferimento a un elemento di superficie emittente:
dI
d EV = 2V cos α.
(1)
r
L'illuminamento in un punto si ottiene integrando a tutta la superficie S della sorgente:
cos α
EV = ∫ 2 d I V .
(2)
S r
4. ILLUMINAZIONE DEGLI AMBIENTI CHIUSI
45
In molti casi pratici la forma e la disposizione spaziale delle superficie emittenti sono tali che il calcolo dell'integrale (2)
può essere fatto senza troppe difficoltà. Per agevolarlo si possono usare
dei diagrammi come quelli riassunti
qui nelle figure (Zijl). L'illuminamento EV in un punto o quello medio su
una superficie o su una linea viene espresso in funzione del flusso luminoso Φ emesso dalla sorgente (anch'essa supposta puntiforme o estesa
su una superficie o su una linea ret- 2. Sorgente verticale; superficie illuminata al pata), di una dimensione lineare h al vimento.
quadrato e di un fattore adimensionale f che viene fornito dai diagrammi per i diversi casi considerati.
La figura 1 si riferisce al caso di una stanza rettangolare di altezza h con una sorgente posta al soffitto e permette di calcolare l'illuminamento direttamente prodotto:
- nel punto N se l'intero soffitto costituisce la sorgente di luce;
- sull'intero pavimento (valore
medio) se la sorgente è puntiforme e si trova in A;
- sul lato MN (valore medio) se
la sorgente è distribuita lungo
lo spigolo AD (p. es. lampada
tubolare fluorescente).
Valgono le seguenti relazioni:
Φ ABCD = fh 2 E N ;
(3)
Φ A = fh E MNPQ ;
(4)
2
3. Sorgente lineare posta lungo uno spigolo al soffitto.
Φ AD = fh 2 E MN ;
(5)
dove EN, EMNPQ, EMN sono i valori (o i valori medii) dell'illuminamento EV nel punto N, sulla superficie MNPQ o sul
segmento MN e ΦA, ΦDA, ΦABCD il flusso luminoso emesso rispettivamente da una
sorgente puntiforme posta in A, da una sorgente lineare (tubo fluorescente) disposta lungo AD o da una sorgente rettangolare ABCD. Il simbolo h indica la distanza
della sorgente dal piano illuminato, come detto; f viene letto sul diagramma 1.
La figura 2 permette di calcolare il valore di EV in un punto N, determinato da una
superficie emittente rettangolare ABQM; dà inoltre il valore di f nella relazione che
lega il flusso emesso da una lampada tubolare AM e l'illuminamento medio sul segmento NP. Valgono le seguenti relazioni:
APPUNTI DI FISICA TECNICA: FOTOMETRIA
46
Φ ABQM = fh 2 E N ;
(6)
Φ AM = fh 2 E NP .
(7)
La figura 3 riguarda il caso di una
lampada tubolare AB parallela alla
superficie illuminata rettangolare
MNPQ. Vale la relazione:
Φ AB = fh 2 E MNPQ .
(8)
La figura 4 infine mette in relazione flusso Φ e illuminamento EV 4. Sorgente rettangolare parallela alla superficie illuminata (soffitto luminoso).
nel caso che la sorgente e la superficie illuminata siano facce opposte di un parallelepipedo (p. es. soffitto e pavimento). Vale la relazione:
Φ ABCD = fh 2 E MNPQ .
(9)
Le relazioni da (3) a (9) assieme alle curve che danno h per i diversi casi permettono di risolvere in modo relativamente agevole un gran numero di problemi, cioè
quelli nei quali la sorgente e la superficie illuminata possono essere validamente
rappresentate con le forme semplici indicate nelle figure.
4.4. Metodo del flusso totale
I procedimenti indicati ai §§ 4.2 e 4.3 consentono, quando siano note le caratteristiche della sorgente, estesa o concentrata, di calcolare l'illuminamento diretto su
una superficie, cioè l'illuminamento prodotto da quella parte del flusso luminoso,
che viene direttamente intercettata dal piano di lavoro. In verità la rimanente parte
del flusso emesso, che incide sulle pareti, sul pavimento, etc., essendo rinviata da
queste superficie per riflessione (di solito diffusa), viene a cadere, direttamente o
dopo altre riflessioni, sul piano di lavoro, pur se attenuata per effetto dell'assorbimento che ha luogo ad ogni riflessione. Un simile processo subisce quella parte del
flusso luminoso incidente sul piano di lavoro, che da questo viene rinviata.
Per una corretta valutazione di questo altro contributo all'illuminamento si dovrebbe applicare ripetutamente la (2) del § 4.3 considerando come sorgenti, dopo la
sorgente primaria, le diverse sorgenti secondarie costituite da tutte le altre superficie presenti nell'ambiente.
Questo procedimento, se esteso alle riflessioni che hanno luogo su tutte le pareti e
sui corpi presenti e a un grande numero di successivi rinvii, risulta piuttosto lento e
faticoso. Inoltre esso è solo apparentemente capace di dare un risultato preciso: infatti il calcolo si basa su ipotesi e schemi (coefficienti di riflessione diffusa perfettamente noti, uniformi su ciascuna superficie e costanti nel tempo; superficie riflettenti perfettamente lambertiane) che sono in realtà veri solo approssimativamente.
D'altra parte, la natura del problema non è tale da richiedere un'alta precisione del
4. ILLUMINAZIONE DEGLI AMBIENTI CHIUSI
47
risultato: una differenza dell'illuminamento di un ambiente del 10% in più o in meno influisce ben poco sul benessere visivo ed è difficilmente apprezzabile senza
strumenti di misura.
Perciò si usa seguire per la fase di progetto il metodo del flusso totale. Questo si
propone di mettere in relazione il flusso luminoso Φ0 emesso dalla sorgente (o
dalle sorgenti) e il flusso luminoso utile ΦU, cioè quello che viene a incidere, direttamente o dopo riflessioni, sulla superficie che interessa illuminare (il piano di
lavoro). Il metodo non dà alcuna notizia sull'uniformità della distribuzione del flusso sul piano di lavoro, anzi si suppone in partenza che una tale uniformità ci sia;
un'eventuale verifica di tale ipotesi deve essere fatta con altre considerazioni.
Supponendo assegnato l'illuminamento medio EV sul piano di lavoro avente area S,
il flusso utile deve essere:
Φ U = EV S .
(1)
Nel calcolo di progetto il valore di EV è un dato del problema, come si è visto al
§ 4.1.1, una volta che sia nota la destinazione del locale.
Quanto alla superficie S, questa viene ordinariamente detta l'area del piano di lavoro, ma nella sua
valutazione deve farsi attenzione: spesso in un ambiente, dove si realizza una illuminazione generale,
sono ubicati diversi posti di lavoro (tavoli, scrivanie, banchi) che vengono a intercettare solo una parte
del flusso luminoso cadente dall'alto, mentre il resto va a incidere sul pavimento; non di meno si deve
prendere come Φ U tutto il flusso che arriva al piano di lavoro ideale, costituito di solito dal piano orizzontale posto all'altezza di 80 cm dal pavimento e di area pari alla superficie in pianta del locale.
Da quanto detto ai paragrafi precedenti è chiaro come, una volta che siano noti il
flusso luminoso Φ0 emesso dalla sorgente o dalle sorgenti, la forma della superficie
fotometrica di ciascun apparecchio illuminante, le dimensioni del locale, la posizione in esso della sorgente (o delle sorgenti, supposte tutte uguali), l'altezza del piano
di lavoro, nonché i valori della albedo relativi al soffitto e alle pareti, è possibile
calcolare l'illuminamento nei vari punti del piano di lavoro e quindi il valore del
flusso utile ΦU. Il rapporto:
Φ
u= U
(2)
Φ0
viene detto coefficiente di utilizzazione.
Si è osservato che il coefficiente di utilizzazione u calcolato per un caso è valido
anche in tutti i casi geometricamente e fotometricamente simili. Le variabili da considerare per questa similitudine sono:
- la forma della superficie fotometrica degli apparecchi illuminanti;
- la forma del locale;
- l'albedo delle superfici delimitanti l'ambiente (pareti, soffitto...);
- la posizione degli apparecchi illuminanti all'interno del locale.
La forma della superficie fotometrica di un apparecchio illuminante viene individuata mediante l'una o l'altra delle classificazioni elaborate dai vari enti normatori
48
APPUNTI DI FISICA TECNICA: FOTOMETRIA
nazionali. Quanto alla forma del locale, questa è descritta sinteticamente dall'indice
del locale i, parametro adimensionale che spesso è definito come:
La Lu
i=
(3)
H (La + Lu )
con:
La = larghezza del locale;
Lu = lunghezza del locale;
H = altezza utile, che è l'altezza delle sorgenti luminose sul piano di lavoro se il
flusso che esse emettono è diretto prevalentemente verso il basso (illuminazione
diretta); se invece il flusso luminoso è inviato prevalentemente verso l'alto per essere riflesso verso il basso dal soffitto (illuminazione diffusa), allora l'altezza utile
è l'altezza del soffitto sul piano di lavoro. Qualunque sia l'altezza e l'orientamento
degli apparecchi illuminanti, si assume poi che questi siano uniformemente distribuiti su tutta la pianta del locale e che conseguentemente sul piano di lavoro si abbia un illuminamento abbastanza uniforme.
Accettando la validità della similitudine, è possibile limitarsi a eseguire una volta
per tutte il calcolo del coefficiente di utilizzazione per un numero adeguato di
combinazioni dei vari parametri sopra individuati (superficie fotometrica di emissione delle sorgenti, albedo del soffitto e delle pareti, indice del locale) e riportare i
risultati in forma di tabelle. Disponendo di queste poi, per risolvere il generico problema che si presenti, basterà individuare nelle tabelle il caso che meglio lo rappresenti e leggere in corrispondenza il valore di u. Noto ΦU = EV S e noto u, si può
calcolare il valore del flusso luminoso che deve essere emesso dalle sorgenti da installare:
Φ
Φ0 = U .
(4)
u
Durante la vita delle lampade il flusso luminoso emesso va diminuendo col tempo
rispetto al valore iniziale (v. § 3.2 per le lampade a incandescenza, ma il fenomeno
si verifica anche per le lampade a scarica). Inoltre della polvere si va depositando
sui corpi trasparenti e sulle superficie riflettenti degli apparecchi illuminanti: questo
è un altro motivo di diminuzione del Φ0 rispetto al valore che si ha con l'impianto
appena installato. Anche la polvere che va ricoprendo le pareti del locale fa diminuire la albedo di queste con l'andar del tempo. Per tenere conto di tutto ciò, il flusso
luminoso che le lampade devono emettere si calcola incrementando il valore di Φ0,
trovato come sopra detto, moltiplicandolo per il fattore di deprezzamento, che è
almeno pari a 1,3 e può arrivare a 1,7 secondo le attività che si svolgono nell'ambiente, le caratteristiche degli apparecchi illuminanti e delle pareti e la cura che verrà prevedibilmente posta nella manutenzione dell'impianto d'illuminazione. In certi
casi il coefficiente u dato dalle tabelle pubblicate tiene già conto del fattore di deprezzamento.
4. ILLUMINAZIONE DEGLI AMBIENTI CHIUSI
49
Varii autori, pur seguendo in sostanza questa stessa impostazione basata sulla similitudine, adottano diverse definizioni dell'indice del locale e diversi modi per tener conto della riflettanza delle pareti e della forma della superficie fotometrica
delle sorgenti. Non si danno altri particolari su tali metodi, che concettualmente
seguono tutti più o meno da vicino l'impostazione cui sopra si è accennato.
BIBLIOGRAFIA
I. BARDUCCI: Fotometria e Colorimetria. ESA, Roma, 1982.
M. COLUMBA, G. LO GIUDICE: Esercizi ed esercitazioni di Fisica Tecnica. Denaro,
Palermo, 1964.
G. MONCADA LO GIUDICE, A. DE LIETO VOLLARO: Illuminotecnica. Masson ESA,
Milano, 1993.
G. PAROLINI, M. PARIBENI: Tecnica dell'illuminazione. UTET, Torino, 1977.
A. SELLERIO: Fisica Tecnica. Vol. II. Pezzino, Palermo, 1951.
50
APPUNTI DI FISICA TECNICA: FOTOMETRIA
INDICE ANALITICO
Abbagliamento: 41
Accenditore: 35
Accomodazione: 3
Acuità visiva: 4
AFE: 40
Albedo: 16, 39, 47
Bastoncelli: 6
Bianco: 5, 24, 42
Brillanza: 4
Candela: 10, 11
Colore: 4, 24, 25, 35, 42
Coni: 6
Contrasto: 39
Corpo nero: 11, 24, 25, 37, 42
Deprezzamento, fattore di -: 48
DIN: 40
Durata media delle lampade: 27, 48
Fattore di forma: 45
Fluorescenza: 2, 34, 35
Flusso luminoso: 9, 11, 21, 25, 45, 47
Footcandle: 15
Footlambert: 13
Fosfòri: 34, 36
Fotometrica, superficie: 11, 15, 20, 23, 47
Fotometro: 18
Fotopica, visione: 6, 7, 14, 25
Hefner, lampada campione di -: 11
IES: 39
Illuminamento: 4, 14, 39, 41, 42, 44
Indice del locale: 48
Innesco della scarica: 29, 31, 34
Intensità dell'emittanza: 11
Intensità luminosa: 10, 18
Intensità media sferica: 11
Iodio: 28
Ionizzazione: 29, 32, 34
Lambert (unità di misura): 13
Lambert, legge di -: 12, 13, 16, 22
Lampade a luce miscelata: 37
Lampade fluorescenti: 24, 35, 36, 41
Luce solare: 25
Lumen: 9, 11
Luminanza: 5, 13, 20, 26, 36, 42
Lunghezza d'onda: 1, 5, 7, 9
Lux: 15
Luxometro: 17
Mercurio, lampade a vapori di -: 33
Nit: 13
Occhio: 2
Onde elettromagnetiche: 1
Paschen, legge di -: 30, 34
Percezione: 4
Persistenza delle immagini: 4
Phot: 15
Piano di lavoro: 39, 41, 42, 44
Planck, legge di -: 26
Puntiforme, sorgente -: 10, 42
Purezza colorimetrica: 5
Purkinje, fenomeno di -: 8
Radianza: 13
Rendimento luminoso: 25, 28, 33
Reticella Auer: 37
Rètina: 3, 6
Richardson-Fermi, effetto: 32
Rifasamento: 32, 34
Rifrazione, indice di -: 1
Saturazione: 4
Scarica, lampade a -: 29, 35
Scotopica, visione: 6, 10
Secondaria, sorgente: 16
Sodio, lampade a vapori di -: 24, 33, 34
Sorgenti a combustione: 37
Sorgenti a incandescenza: 26, 28
Starter: 32
Stilb: 13
Temperatura di colore: 24, 25, 42
Tinta: 4, 24
Ulbricht, sfera di: 21
Utilizzazione, coefficiente di -: 47
Visibilità, curve normali di -: 7, 9, 17
Wien, legge di -: 24, 26, 37
Wolframio: 26
Xeno, lampade allo -: 35
Zavorra: 30, 34
Zijl, diagrammi di -: 45