Alessandro Farini: Dispense di Illuminotecnica per le scienze della visione
Capitolo 1 Radiazione elettromagnetica e occhio
In questo capitolo prendiamo in considerazione alcune grandezze
fondamentali riguardanti l’illuminazione e alcuni concetti legati
alla visione umana che possono risultare utili per chi deve
occuparsi di aspetti ergonomici.
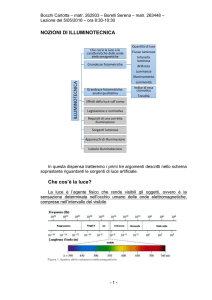
1.1 Lo spettro elettromagnetico
La radiazione visibile è solo una piccola parte dello spettro
elettromagnetico. Quando utilizziamo una qualunque sorgente
luminosa generalmente siamo esposti, oltre alle radiazioni visibili,
anche ad altre radiazioni, come l’ultravioletto e l’infrarosso, che
possono essere assorbite dai mezzi oculari, anche se non sono in
grado di provocare la sensazione visiva. Alcuni dei parametri che
permettono di distinguere tra loro le varie radiazioni
elettromagnetiche sono la lunghezza d’onda λ (Fig.1.1) e la
frequenza ν.
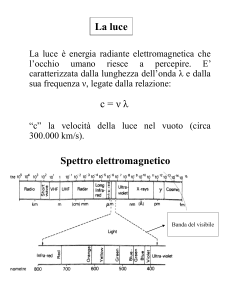
Fig.1.1 Definizione di lunghezza d’onda
La lunghezza d’onda λ e la frequenza ν di una radiazione
elettromagnetica sono grandezze legate tra loro, dato che
possiamo scrivere che, nel vuoto:
# !" = c
dove con c abbiamo indicato la velocità della radiazione nel vuoto
(circa 300.000 Kilometri al secondo). Questa formula ci dice che
radiazioni di lunghezza d’onda più grande hanno frequenza
minore rispetto a radiazioni di lunghezza d’onda più corta.
Se poi ricordiamo la formula di Planck, che ci fornisce l’energia di
un quanto (in pratica un “pacchetto”) di radiazione
elettromagnetica:
E = h!
ne segue che:
c
E=h
!
Abbiamo quindi che l’energia di una radiazione è inversamente
proporzionale alla sua lunghezza d'onda λ; più corta è la
lunghezza d’onda di una radiazione, e maggiore sarà il suo
Istituto Nazionale di Ottica Applicata-CNR
Alessandro Farini: Dispense di Illuminotecnica per le scienze della visione
contributo energetico. E’ necessario dedicare molta attenzione alla
radiazione UV, che, avendo lunghezza d’onda minore rispetto al
visibile presenta di conseguenza un contenuto energetico
maggiore.
1.2 Grandezze radiometriche e fotometriche
Quando si ha a che fare con una grandezza fisica da esaminare in
maniera quantitativa ci si deve per prima cosa chiedere quali siano
le grandezze e le metodiche di misura da poter applicare.
E' esperienza comune che la radiazione luminosa trasporti energia,
infatti essa è in grado di riscaldare i corpi con cui arriva in
contatto, producendo un aumento dell'energia cinetica degli atomi.
Considereremo ora lo studio del trasporto di questa energia da un
duplice punto di vista, quello della radiometria e quello, più
direttamente correlato con la visione umana, della fotometria. La
radiometria è la misura della radiazione elettromagnetica avente
una frequenza compresa tra i 3x1011 fino ai 3 x1016 Hz. Questo vuol
dire prendere in considerazione la radiazione avente lunghezza
d'onda compresa tra i 10 nm e i 1000 micron, appartenente alle
1
0,9
RISPOSTA FOTOPICA
RISPOSTA SCOTOPICA
0,8
RISPOSTA RELATIVA
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0
380
400
420
440
460
480
500
520
540
560
580
600
620
640
660
680
700
720
740
760
780
LUNGHEZZA D'ONDA (nm)
Fig.1.2 Curve di sensibilità dell’occhio umano in visione fotopica e scotopica
regioni dette dell'ultravioletto, del visibile e dell'infrarosso.
La fotometria studia l’effetto della radiazione nella visione umana.
Essa si occupa quindi della radiazione all'interno dell'intervallo di
lunghezza d’onda compresa tra 380 e 780 nm, intervallo di
sensibilità del sistema visivo. L’occhio umano non è sensibile in
maniera
identica
alle
radiazioni
comprese
all’interno
dell’intervallo 380-780 nm: la sensibilità è molto grande nella zona
del giallo-verde, mentre assume valori bassi nel blu e nel rosso.
Tali valori sono rappresentati dalla funzione V(λ) (Fig.1.2) che
misura l’efficienza visuale a varie lunghezze d'onda nel caso di
luminosità diurna (visione fotopica). Essa è normalizzata al
Istituto Nazionale di Ottica Applicata-CNR
Alessandro Farini: Dispense di Illuminotecnica per le scienze della visione
massimo valore V(λ)=1 relativo alla lunghezza d'onda di 555,02
nm. Questa funzione, basata su un campione di circa 200 persone,
è stata internazionalmente accettata, anche se recentemente vi è
molta discussione sulla sua effettiva correttezza. Una differente
funzione V’(λ) misura l’efficienza dell'occhio nel caso di un livello
di luce inferiore, tipico della visione notturna. In queste condizioni
(visione scotopica) il valore 1 si ha per la lunghezza d’onda di 507
nm. Lo spostamento del massimo di sensibilità, dovuto all'utilizzo,
da parte dell'occhio, prima di coni e poi di bastoncelli, è
denominato effetto Purkinije. I bastoncelli, che funzionano in
condizioni di bassa visibilità, vedono meglio il blu di quello che
fanno i coni, i quali possono vedere luce profondamente rossa,
luce che per i bastoncelli appare nera. Se si hanno due pezzi di
carta colorata rossa e blu, con il primo più luminoso del secondo in
condizioni di buona luminosità, passando all'oscurità l'effetto si
inverte.
Come vedremo le grandezze radiometriche e fotometriche sono
assai simili e anche i simboli usati sono talvolta uguali. Si ricorre
quindi, quando possa esservi ambiguità, ad una “e” sottoscritta
per le grandezze radiometriche e ad una “v” per le grandezze
fotometriche.
Grandezze radiometriche: misurano grandezze relative a tutte le
radiazioni elettromagnetiche. Grandezze fotometriche: misurano
grandezze relative alla radiazione visibile (380-780 nm) pesandole
secondo la curva di sensibilità dell’occhio umano V(λ).
Nel fare le misure radiometriche e fotometriche immagineremo di
avere a disposizione un ricevitore integrale, da cui sia possibile
ricavare l’energia assorbita dal corpo. In questo senso la prima
grandezza radiometrica che possiamo definire è l'energia totale (o
raggiante) Q che corrisponde all'energia che arriva
complessivamente sul ricevitore e che si misura in Joule.
L’equivalente grandezza fotometrica è l’energia luminosa (talvolta
chiamata quantità di luce).
Il flusso raggiante Φ è dato dal rapporto tra l'energia totale Q e il
tempo necessario al corpo per ricevere una tale energia. Il flusso
raggiante ha le dimensioni di una potenza e si misura in Watt (W).
dQ
"=
dt
L’equivalente fotometrico è il flusso luminoso che corrisponde alla
luce che viene emessa da una sorgente in tutto lo spazio nell’unità
di tempo (Fig.1.3). Per mettere in connessione le grandezze
fotometriche e quelle!radiometriche si definisce il lumen (lm) (unità
fotometrica del flusso luminoso) in modo tale che 1 Watt di
radiazione emesso a 555,02 nm produca un flusso luminoso di 683
Istituto Nazionale di Ottica Applicata-CNR
Alessandro Farini: Dispense di Illuminotecnica per le scienze della visione
Lumen. Un Watt di radiazione emesso a lunghezze d’onda diverse
produrrà meno di 683 Lumen, dato che la sensibilità del nostro
occhio è massima a 555,02 nm.
Quesito: si ha una lampada che emette 2 Watt di radiazione a 555 nm e 3
W a 820 nm. Quanti Lumen vengono emessi da questa lampada?
Risposta: i due Watt emessi a 555 producono ciascuno 683 Lm. Quindi
683X2=1366. Invece i tre Watt emessi a 820 nm producono 0 Lumen,
poiché la sensibilità dell’occhio umano a quella lunghezza d’onda è zero. I
Lumen prodotti in totale sono quindi 1366.
Se definiamo un fattore di conversione KM=683 lm/W allora
possiamo passare dal flusso energetico al flusso luminoso
moltiplicando per la sensibilità dell’occhio umano e per il fattore
di conversione:
780 nm
#v = KM
" # e (! )V (! )d!
380 nm
Si moltiplicano i Watt emessi spettralmente per la sensibilità
dell’occhio tenendo conto del fattore di conversione. Nel caso della
visione scotopica il fattore di conversione è K’M=1700 lm/W a 507
nm, infatti i bastoncelli sono molto più sensibili alla luce rispetto ai
coni.
Fig.1.3 Rappresentazione schematica del flusso luminoso
Il Lumen non è l’unità di misura fondamentale per il sistema
internazionale (SI). Infatti l’unità di misura fondamentale in campo
fotometrico è la Candela (Cd) che permette di misurare l’Intensità
Luminosa Iv. Possiamo definire l’Intensità luminosa come il flusso
luminoso per unità di angolo solido1 in una certa direzione
d" v
Iv =
d!
1
L'angolo solido corrisponde all'apertura di un cono, e lo si misura in termini di rapporto tra l'area della
porzione di superficie intercettata su una sfera con centro nel vertice del cono e il quadrato del raggio
della sfera stessa. La porzione di area che sottende uno steradiante (sr) corrisponde a 1/4π della
superficie della sfera stessa.
Istituto Nazionale di Ottica Applicata-CNR
Alessandro Farini: Dispense di Illuminotecnica per le scienze della visione
(Se al posto delle grandezze fotometriche sostituiamo le grandezza
radiometriche otteniamo l’intensità radiante Ie). La Candela è
definita come l’intensità luminosa, in una data direzione, di una
sorgente che emette radiazione monocromatica di frequenza
540.1012 Hertz e che ha un’intensità radiante in quella direzione di
1/683 Watt/Steradiante. La definizione appare complessa, ma solo
perché deriva direttamente dalla direzione del Lumen [NIST] (la
radiazione di 540.1012 Hertz è quella che coincide nel vuoto ai 555
nm del picco di sensibilità dell’occhio umano). Questa definizione
del 1979 ha sostituito le precedenti definizioni basate
sull’emissione dei corpi neri.
Un’altra grandezza di rilevante importanza è l’illuminamento E
che corrisponde al flusso luminoso che arriva su una unità di area:
d!
E=
dA
La sua unità di misura sono i Lux, che corrispondono quindi ai
Lm/m2.
Fig.1.4 Definizioni della Candela e del Lux
Sull’illuminamento è necessario fare alcune considerazioni di tipo
geometrico. Consideriamo una sorgente puntiforme isotropa (cioè
che emette allo stesso modo in tutte le direzioni) che emette un
flusso luminoso Φ. Se prendiamo una superficie di area unitaria a
una distanza r1 avremo che l’illuminamento su tale superficie sarà
"
E1 =
4!r12
mentre se spostiamo la superficie unitaria a una distanza r2
avremo un illuminamento uguale a
"
E2 =
4!r22
Se a questo punto dividiamo tra loro le due equazioni appena
trovate, tenendo conto che il flusso è lo stesso, otteniamo
Istituto Nazionale di Ottica Applicata-CNR
Alessandro Farini: Dispense di Illuminotecnica per le scienze della visione
E1 r22
=
(*)
E2 r12
da cui si evince che l’illuminamento è proporzionale all’inverso del
quadrato della distanza dalla sorgente. Per questa ragione
raddoppiare la distanza di una superficie da una sorgente equivale
a ridurre a un quarto l’illuminamento.
E1 r22
=
L’equazione
viene chiamata legge dell’inverso del
E2 r12
quadrato e vale a rigore per le sorgenti puntiformi.
Quesito: un libro si trova a 1 metro da una sorgente. L’illuminamento
misurato sul libro è di 90 Lux. Se spostiamo il libro a 3 metri dalla
sorgente, quale sarà l’illuminamento sul libro stesso.
Risposta: E’ possibile risolvere l’esercizio inserendo i dati nell’equazione
(*). Più semplicemente, dato che la distanza è aumentata tre volte
l’illuminamento dovrà diventare un nono e quindi sarà di 10 Lux.
Come grandezza radiometrica, l'irraggiamento (o irradianza) E è il
rapporto tra il flusso raggiante che arriva su una certa superficie e
la superficie stessa e si misura in Watt/m2.
La luminanza L caratterizza invece l'emissione di una sorgente
estesa in una certa direzione. Essa è data dal rapporto tra il flusso
luminoso Φ emesso da un elemento S di superficie di una sorgente
di luce estesa entro un elemento di angolo solido Ω intorno alla
direzione data e il prodotto dell’angolo solido Ω con l’area
apparente della sorgente in quella direzione secondo la formula
d 2"
L=
d#dS cos $
in cui θ è l'angolo formato tra la direzione in cui si va ad
investigare la radiazione e la normale alla superficie emittente.
L’unità di misura della luminanza sono le Cd/m2, anche detta Nit.
! la luminanza di una superficie a riflessione
Quando si considera
diffusa, essa è proporzionale all'illuminamento ed al grado di
riflessione della superficie.
Un argomento di ricerca di grande interesse tutt’ora è la relazione
tra la luminanza e la brillanza, che corrisponde alla sensazione
soggettiva associata alla percezione dell’intensità di un fasci
luminoso. Tale relazione non è necessariamente lineare,
soprattutto nelle zone di bassa o molto alta luminanza.
Legge del coseno e area apparente
Danni oculari
Istituto Nazionale di Ottica Applicata-CNR