1.Il modello elettrico del modulo
La caratteristica I(V) di yuna calla PV è:
I(V) = Isc-Io[exp(V/(VT))-1]= Isc-Io[exp(V/VT)-1]=
con VT=n.0,026V a T=273 K (n =1÷4) coefficiente del diodo
IL
IL
Rs
a)
IL
Rs
? 0,6 V
Rs
? 0,6 V
? 0,6 V
Diodo by -pass
I Isc
b)
0,6 V 0
Modulo PV
+
Mod. PV c) V
ON
Mod. PV
OFF
V
V oc
+
I
Simbolo
del modulo PV
(incluso
diodo by -pass)
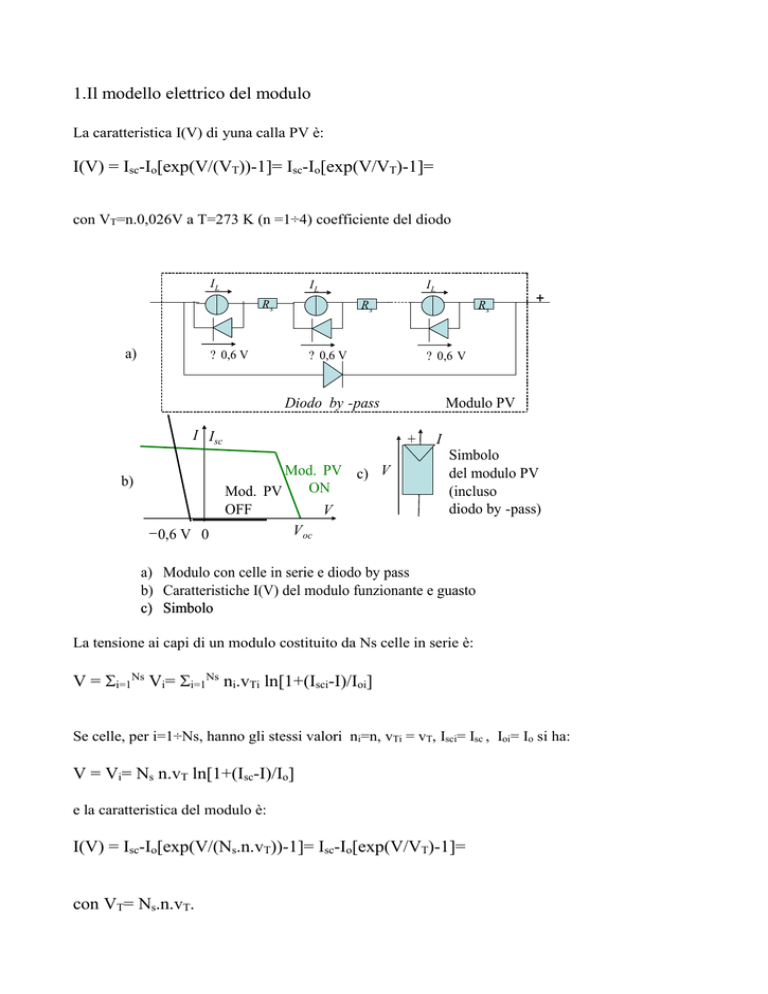
a) Modulo con celle in serie e diodo by pass
b) Caratteristiche I(V) del modulo funzionante e guasto
c) Simbolo
La tensione ai capi di un modulo costituito da Ns celle in serie è:
V = i=1Ns Vi= i=1Ns ni.vTi ln[1+(Isci-I)/Ioi]
Se celle, per i=1÷Ns, hanno gli stessi valori ni=n, vTi = vT, Isci= Isc , Ioi= Io si ha:
V = Vi= Ns n.vT ln[1+(Isc-I)/Io]
e la caratteristica del modulo è:
I(V) = Isc-Io[exp(V/(Ns.n.vT))-1]= Isc-Io[exp(V/VT)-1]=
con VT= Ns.n.vT.
Nel caso di un modulo con Nc =Ns.Np celle identiche, di cui Np in parallelo per ogni blocco, si ha:
I(V) = NpIsc1- Np Io1[exp(V/(Ns.n.vT))-1]
ciascuna con corrente di corto circuito Isc1 e corrente di saturazione Io1.
Per un modulo generico, con il modello a diodo, si ha:
I(V) = Isc- Io[exp(V/(VT))-1]
in cui Isc= NpIsc1, Io= Np Io1 e VT=Ns.n.vT .
Prendendo come riferimento i valori nelle condizioni STC (Go =1 kWh/m2, To=25oC) la corrente
di corto circuito Isc, la tensione a vuotoVoc e la tensione termica VT , nelle condizioni di
funzionamento (G, Tc) valgono (con espressioni analoghe a quelle della singola cella):
Isc = Isc(G,Tc) = IscoG [1+I (Tc-To)]
Voc = Voc (G,Tc) = Voco + VTolnG+V(Tc-To)
VT =VT (G,Tc) = VTo(Tc+273)/298 = Ns.n.vTo(Tc+273)/298
ove Isco e Voco sono la corrente in corto circuito e la tensione a vuoto nelle condizioni STC, I è il
coefficiente di temperatura (positivo) della Isc e V il coefficiente (negativo) di Voc (Fig.5.6.)
VTo è ricavabile anche dal punto di massima potenza (IMo, VMo) del modulo nelle condizioni STC:
VTo ≈ (VMo-Voco)/ln(1-IMo/Isco)
Quest’espressione permette, in particolare, di calcolare il coefficiente diodo n in quanto V To=
0,026.n Ns.
2. Ottimizzazione del funzionamento su carico resistivo
Per massimizzare il rendimento energetico del modulo è necessario farlo funzionare nel punto di
massima potenza (Maximum Power Point: MPP) la cui tensione è:
VM= Voc-VTln(1+VM/VT)
Se voc=Voc/VT >10 si può utilizzare l’espressione approssimata di FF:
FF= (voc-ln(voc +0,72))/(1+ voc),
con errori minori dello 0,01% (Tabella I Cap.La potenza massima è:
PM= Isc.Voc.FF
dove i valori sono calcolati nelle effettive condizioni operative.
MPP è caratterizzabile dalla resistenza di massimo trasferimento (RM=VM/IM) che dipende dalle
condizioni ambientali mentre il carico (resistenza R L) è generalmente predeterminato. È quindi
necessario introdurre un “trasformatore” dei fattori elettrici che permetta al modulo di “vedere “
sempre la resistenza ottima RM.
Il convertitore DC/DC è il dispositivo elettrico che permette questa trasformazione; se I,V e IL,VL
sono rispettivamente i fattori elettrici in ingresso ed in uscita si ha nel caso ideale (assenza di
dissipazione di potenza nel DC/DC) I.V = IL.VL e, in particolare V2/R=VL2/RL.
Se il DC/DC è basato su un modulatore a larghezza di impulso (Pulse Width Modulator: PWM)
dalla sua analisi si ha:
V/VL = (1-d)/d e quindi R= RL[d/(1-d)]2
dove d è il duty cycle del PWM; con un opportuno valore di d si ottiene la trasformazione dei
fattori elettrici rappresentati dai punti PM (cerchietto grigio) e PRL (cerchietto vuoto) della
caratteristica, a iperbole, del convertitore DC/DC (Fig. 5.7.b).
IV=IMVM
+
con MPPT
senza MPPT
I
V
R
PWM
Cuk
PM
VL
RL
I
PRL
R
RL
Principio
di funzionamento del
V=VL(1-d)/d
convertitore
DC/DC
d duty cycle
del PWM
(PulseCuk:
Width
VL = V·d/(1 d); da cui R= RL(1 d)/d
Modulator)
d (duty cycle):
R = 0 DC/DC
per d = 0a rapporto
R = ∞ per
d=1
a) Convertitore
variabile
V
b) Caratteristica con punto
di lavoro variabile
a) Resistore variabile (Conv. DC/DC e RL)
3. Modelli per la stima della potenza massima
La stima della potenza massima PM (G,Tc) nelle condizioni operative (G,Tc) è il primo passo per la
valutazione della resa energetica del modulo. Per questo si possono utilizzare le espressioni del
modello elettrico a diodo con i dati del costruttore in una delle seguenti forme:
A) PM (G,Tc) =
B) PM (G,Tc) =
C) PM (G,Tc) =
D) PM (G,Tc) =
Isc(G,To).Voc(G,To) ).FF(G,To)[1+(Tc-To)]
Isc(G,Tc).Voc(G,Tc) ).FF(G,Tc)
IM(G,To).VM(G,To).[1+(Tc-To)]
IM(G,Tc).VM(G,Tc)
dove [%/oC] è il coefficiente di temperatura della potenza massima.
Le espressioni A) e B) sono valide solo se lo è la formula approssimata per il calcolo di FF. Le
espressioni B) e D) permettono il confronto con le misure in campo.
Le espressioni sono state utilizzate in una simulazione con un modulo al silicio cristallino (c-Si) ed
uno al silicio amorfo (a-Si) per irradiazioni G=200÷1250 W/m2 e temperature ambiente
Ta=10÷35oC; nel primo caso si sono utilizzati i quattro metodi mentre per il silicio amorfo non è
stato possibile utilizzare l’espressione approssimata di FF. In Tabella 5-II sono riportati i risultati di
alcune simulazione: i valori medi (a) e gli scarti dei diversi metodi (b).
G(W/m2)
200
800
1250
Modulo c-Si
Ta(oC)
10
25
35
13,4 12,5
59,1 55,1 52,5
84,8 80,5
Modulo a-Si
Ta(oC)
10
25
35
7,6
7,1
46,0 43,9 42,5
75,8 73,5
Tabella 5-IIa Esempi di simulazione di potenze massime in diverse condizioni ambientali
Media
Scarto%
A-B c-Si
50,71
1,56
C-D c-Si
51,56
0,09
C-D a-Si
42,35
1,09
Tabella 5-IIb Scarti delle simulazioni
Le precedenti espressioni sono tutte basate sul modello a diodo che, sperimentalmente, è
stato verificato non essere sufficientemente preciso per un’ampia gamma di condizioni
ambientali reali.
Si presentano perciò tre modelli che esprimono la massima potenza erogabile nelle condizioni
ambientali (G, Tc): il primo è un modello della corrente e tensione nel punto di massima potenza, il
secondo si basa esclusivamente su considerazioni energetiche, il terzo è un ibrido dei due
precedenti.
Il modello di Heydenreich /2/
Il modello quantifica le potenze in gioco nel modulo dovute a: un generatore di corrente/tensione e
due dissipatori di potenza rispettivamente di tipo serie e parallelo.
La corrente e la tensione sono modellate con generatori proporzionali rispettivamente alla
radiazione G (in analogia alla corrente Isc del modello a diodo), e a lnG (in analogia alla Voc del
modello a diodo). La potenza generata dal modulo è quindi la somma di tre contributi:
PM =aG.lnG+bln2G+c G2
per cui la potenza massima nelle condizioni ambientali (G,Tc) è espressa da:
PM (G,Tc) = [aG ln(G+1) + bG2+cln²(G+1)](1+(Tc-To) =PM(G,25)(1+(Tc-To)
dove i parametri, a,b, c sono misurati per diversi valori di G e Tc=To mentre per si potrebbe
utilizzare una singola misura ad una particolare temperatura Tc o il dato di targa. Il modello è
semplice in quanto richiede solo tre parametri, per le condizioni STC.
Il modello Friesen/3/
È un ibrido dei precedenti modelli; MPP è definito da:
IM = Imo.G.[1+IM (Tc-To)]
VM =Vmo+C0.lnG +C1.ln2G+VM.(Tc-To)
IM e VM sono i coefficienti di corrente e temperatura in MPP nelle condizioni G=1 kW/m2 e
To=25oC.
La potenza massima nelle condizioni (G,Tc) è:
PM(G,Tc)=IMVM= Imo.G [Vmo+C0.lnG +C1.ln2G+VM.(Tc-To)] .[1+IM (Tc-To)]
e nelle condizioni (G,To):
PM(G,To)=IMoG(VMo+C0lnG +C1ln2G)= PmoG+C0. IMo GlnG + C1IMo G ln2G
che richiede solo la determinazioni di C0 e C1 se si hanno i dati di targa di IMo, VMo, IM, VM,.
Nelle condizioni operative si ha:
PM(G,Tc)=IMVM= [PM(G,2To) +VM. IMoG Tc-To)] .[1+IM.(Tc-To)]
E’ proposta anche l’espressione della temperatura della cella:
Tc=T+1,25.(NOST-20)G+Ta
con T ≈ 2oC sovratemperatura della cella rispetto al retro del modulo (NOST: Nominal Operating
Specific Temperature).
Ad es. per il modulo Sunpower STM210 F le misure hanno dato:
IMo=5,2 A; VMo= 39,5 V; IM=-1,21.10-4/oC; VM= -0,181V/oC; C0= -1,52V; C1= -1,57V e NOST
= 42.7oC
La Tabella 5-III riassume le caratteristiche dei quattro metodi a cui si rimanda per il calcolo delle
espressioni della potenza massima
Modelli
Espressione
diodo King
Heydenreich
si
si
PM(G,To)[1+(Tc-To)]
PM(G,Tc)
si
si
Tabella 5-III Applicabilità die metodi di stima della potenza
Friesen
si
Per valutare l’effetto della temperatura ambiente e della irradiazione G sul funzionamento del
modulo si è definito il parametro NOCT (Nominal Operating Cell Temperature).
NOCT è la temperatura della cella più calda di un modulo a circuito aperto (cioè la situazione
termicamente peggiore) nelle condizioni normalizzate di G=0,800 kW/m2, temperatura ambiente di
20 °C e velocità del vento di 1 m/s.
Per una generica condizione si ha:
Tc (G,Ta) = 1,25.(NOCT-20)G+Ta
Per cui si può calcolare la potenza massima PM(G,Ta) = PM(G,Tc) utilizzando la precedente
relazione.