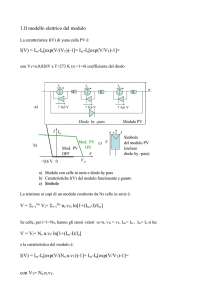
STIMA DELLA POTENZA DISPONIBILE DA UN MODULO FOTOVOLTAICO
La stima della potenza massima PM (G,Tc) è il primo passo per la valutazione della resa energetica
del modulo. Per questo si possono utilizzare le espressioni del modello elettrico a diodo con i dati
del costruttore in una delle seguenti forme:
A) PM (G,Tm) =
B) PM (G,Tm) =
C) PM (G,Tm) =
D) PM (G,Tm) =
Isc(G,To).Voc(G,To) ).FF(G,To)[1+(Tm-To)]
Isc(G,Tm).Voc(G,Tm) ).FF(G,Tm)
IM(G,To).VM(G,To).[1+(Tm-To)]
IM(G,Tm).VM(G,Tm)
dove [%/oC] è il coefficiente di temperatura della potenza massima.
Le espressioni A) e B) sono valide solo se lo è la formula approssimata per il calcolo di FF, ma
utilizzano i dati di targa del modulo, sempre disponibili. L’espressione C) richiede la risoluzione di
un’equazione trascendente e la D) richiede informazioni generalmente non disponibili.
ESERCITAZIONE 1)
Modello a un diodo (One Diode Model) (Green):
A) con dati nelle condizion STC:
PM(G,Tm) = IscoG.( Voco + VTolnG) FF(G,To) [1+(Tm-To)]
e VTo ≈ (VMo-Voco)/ln(1-IMo/Isco);
se voco=Voco/VT >10 si può utilizzare l’espressione approssimata di FF:
FF(G,To)= (voc-ln(voc +0,72))/(1+ voc),
B) con dati nelle condizioni (G,Tm):
PM(G,Tm) = IscoG.(1+(Tm-To))Voc(G,Tm) FF(G,Tm)
Tm = Ta+(NOCT-20)G/800
VTo ≈ (VMo-Voco)/ln(1-IMo/Isco)
Voc(G,Tm)=(Voco + VTolnG)(1+(Tm-To))
VT(Tm) ≈ VTo(273+Tm)/298 ;
voc(Tm)= Voc(G,Tm)/ VT(Tm) per voc( Tm >5 si può utilizzare l’espressione approssimata di FF
con un errore dell’1%:
FF(G,Tm)= [voc(Tm)-ln(voc(Tm) +0,72)]/(1+ voc(Tm)),
C) Ha il vantaggio che non è necessario il calcolo approssimato di FF, ma i deve calcolare, con la
corrispondente equazione, VM(G,To) e quindi IM(G,To).
Parametri da utilizzare, per il confronto dei modelli con i dati sperimentali di ISAAC
Module
Code
Pm [W]
Im [A]
Vm [V]
Isc [A]
Voc [V]
FF
[%]
γ
[%/°C]
[%/°C]
[%/°C]
Sharp NA-851WQ
Data Sheet
misurati
85,0
86.91
1,74
1.814
49,0
47.9
2,11
2.238
63,8
62.939
63,3
61.7
-0,24
-0.3307
0,07
-0,30
ESERCITAZIONE 2) (non ancora definita)
Il modello a diodo non è sufficientemente preciso per un’ampia gamma di condizioni
ambientali reali.
Si presentano perciò due modelli che esprimono la massima potenza erogabile nelle condizioni
ambientali (G, Tc): il primo è un modello della corrente e tensione nel punto di massima potenza, il
secondo si basa esclusivamente su considerazioni energetiche, il terzo è un ibrido dei due
precedenti.
Il modello di Heydenreich
Il modello quantifica le potenze in gioco nel modulo dovute a: un generatore di corrente/tensione e
due dissipatori di potenza rispettivamente di tipo serie e parallelo.
La corrente e la tensione sono modellate con generatori proporzionali rispettivamente alla
radiazione G (in analogia alla corrente Isc del modello a diodo), e a lnG (in analogia alla V oc del
modello a diodo). La potenza generata dal modulo è quindi la somma di tre contributi:
PM =aG.lnG+bln2G+c G2
per cui la potenza massima nelle condizioni ambientali (G,Tc) è espressa da:
PM (G,Tc) = [aG ln(G+1) + bG2+cln²(G+1)](1+(Tc-To) =PM(G,25)(1+(Tc-To)
dove i parametri, a,b, c sono misurati per diversi valori di G e Tc=To mentre per si potrebbe
utilizzare una singola misura ad una particolare temperatura Tc o il dato di targa. Il modello è
semplice in quanto richiede solo tre parametri, per le condizioni STC.
Il modello ISAAC
È un ibrido dei precedenti modelli; MPP è definito da:
IM = Imo.G.[1+IM (Tc-To)]
VM =Vmo+C0.lnG +C1.ln2G+VM.(Tc-To)
IM e VM sono i coefficienti di corrente e temperatura in MPP nelle condizioni G=1 kW/m2 e
To=25oC.
La potenza massima nelle condizioni (G,Tc) è:
PM(G,Tc)=IMVM= Imo.G [Vmo+C0.lnG +C1.ln2G+VM.(Tc-To)] .[1+IM (Tc-To)]
e nelle condizioni (G,To):
PM(G,To)=IMoG(VMo+C0lnG +C1ln2G)= PmoG+C0. IMo GlnG + C1IMo G ln2G
che richiede solo la determinazioni di C0 e C1 se si hanno i dati di targa di IMo, VMo, IM, VM,.
Nelle condizioni operative si ha:
PM(G,Tc)=IMVM= [PM(G,2To) +VM. IMoG Tc-To)] .[1+IM.(Tc-To)]