5. Misure sui moduli

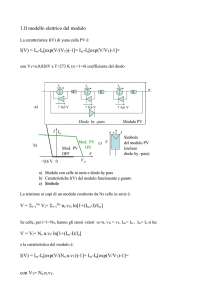
1. Modello elettrico del modulo
La tensione ai capi di un modulo costituito da Ns celle in serie è:
V = i=1Ns Vi= i=1Ns ni.vTi ln[1+(Isci-I)/Ioi]
dove si è utilizzato il modello a diodo.
Se celle, per i=1÷Ns, hanno gli stessi valori ni=n, vTi = vT, Isci= Isc , Ioi= Io si ha:
V = Vi= Ns n.vT ln[1+(Isc-I)/Io]
e la caratteristica del modulo è:
I(V) = Isc-Io[exp(V/(Ns.n.vT))-1]= Isc-Io[exp(V/VT)-1]=
con VT= Ns.n.vT.
Nel caso di un modulo con Nc =Ns.Np celle identiche, di cui Np in parallelo per ogni
blocco, si ha:
I(V) = NpIsc1- Np Io1[exp(V/(Ns.n.vT))-1]
ciascuna con corrente di corto circuito Isc1 e corrente di saturazione Io1.
Per un modulo generico, con il modello a diodo, si ha:
I(V) = Isc- Io[exp(V/(VT))-1]
in cui Isc= NpIsc1, Io= Np Io1 e VT=Ns.n.vT .
Prendendo come riferimento i valori nelle condizioni STC (Go =1 kWh/m2,
To=25oC) la corrente di corto circuito Isc, la tensione a vuotoVoc e la tensione termica
VT , nelle condizioni di funzionamento (G, Tc) valgono (con espressioni analoghe a
quelle della singola cella):
Isc = Isc(G,Tc) = IscoG [1+I (Tc-To)]
Voc = Voc (G,Tc) = Voco + VTolnG+V(Tc-To)
VT =VT (G,Tc) = VTo(Tc+273)/298 = Ns.n.vTo(Tc+273)/298
ove Isco e Voco sono la corrente in corto circuito e la tensione a vuoto nelle condizioni
STC, I è il coefficiente di temperatura (positivo) della Isc e V il coefficiente
(negativo) di Voc (Fig.5.6.)
VTo è ricavabile anche dal punto di massima potenza (IMo, VMo) del modulo nelle
condizioni STC:
VT ≈ (VMo-Voco)/ln(1-IMo/Isco)
Quest’espressione permette, in particolare, di calcolare il coefficiente diodo n in
quanto VTo= vTo .n.Ns = 0,026.n Ns.
2. Modelli per la stima della potenza massima
La stima della potenza massima PM (G,Tc) nelle condizioni operative (G,Tc) è il
primo passo per la valutazione della resa energetica del modulo. Per questo si
possono utilizzare le espressioni del modello elettrico a diodo con i dati del
costruttore in una delle seguenti forme:
A) PM (G,Tc) =
B) PM (G,Tc) =
C) PM (G,Tc) =
D) PM (G,Tc) =
Isc(G,To).Voc(G,To) ).FF(G,To)[1+(Tc-To)]
Isc(G,Tc).Voc(G,Tc) ).FF(G,Tc)
IM(G,To).VM(G,To).[1+(Tc-To)]
IM(G,Tc).VM(G,Tc)
dove  [%/oC] è il coefficiente di temperatura della potenza massima.
Le espressioni A) e B) sono valide solo se lo è la formula approssimata per il calcolo
di FF. Le espressioni B) e D) permettono il confronto con le misure in campo.
Le espressioni sono state utilizzate in una simulazione con un modulo al silicio
cristallino (c-Si) ed uno al silicio amorfo (a-Si) per irradiazioni G=200÷1250 W/m2 e
temperature ambiente Ta=10÷35oC; nel primo caso si sono utilizzati i quattro metodi
mentre per il silicio amorfo non è stato possibile utilizzare l’espressione approssimata
di FF. In Tabella 5-II sono riportati i risultati di alcune simulazione: i valori medi (a)
e gli scarti dei diversi metodi (b).
G(W/m2)
200
800
1250
Modulo c-Si
Modulo a-Si
o
Ta( C)
Ta(oC)
10
25
35
10
25
35
13,4 12,5
7,6 7,1
59,1 55,1 52,5 46,0 43,9 42,5
84,8 80,5
75,8 73,5
Tabella 5-IIa Esempi di simulazione di potenze massime in diverse condizioni
ambientali
A-B c-Si
C-D c-Si
Media Scarto%
50,71
1,56
51,56
0,09
C-D a-Si
42,35
1,09
Tabella 5-IIb Scarti delle simulazioni
Le precedenti espressioni sono tutte basate sul modello a diodo che,
sperimentalmente, è stato verificato non essere sufficientemente preciso per
un’ampia gamma di condizioni ambientali reali, ma è una prima
approssimazione per formule sperimentalmente più collaudate. Infatti:
PM (G,Tc) = Isc(G,To).Voc(G,To) ).FF(G,To)[1+(Tc-To)]=
= IscoG. (Voco+VTolnG) FF(G,To)[1+(Tc-To)]=
= (PMoG+PMoGlnG)[1+(Tc-To)]
dove PMo e  sono valori in condizioni STC, PMo può essere calcolato dai
parametri SCT oppure determinato sperimentalmente.
Si presentano ora tre modelli della massima potenza nelle condizioni
ambientali (G, Tc) che come si vedrà aggiungono termini correttivi al risultato
precedente “teorico”: il primo è un modello della corrente e tensione nel punto
di massima potenza, il secondo si basa esclusivamente su considerazioni
energetiche, il terzo è un ibrido dei due precedenti.
Il modello di Heydenreich /2/
Il modello quantifica le potenze in gioco nel modulo dovute a: un generatore di
corrente/tensione e due dissipatori di potenza rispettivamente di tipo serie e parallelo.
La corrente e la tensione sono modellate con generatori proporzionali rispettivamente
alla radiazione G (in analogia alla corrente Isc del modello a diodo), e a lnG (in
analogia alla Voc del modello a diodo). La potenza generata dal modulo è quindi la
somma di tre contributi:
PM =aG.lnG+bln2G+c G2
per cui la potenza massima nelle condizioni ambientali (G,Tc) è espressa da:
PM (G,Tc) = [aG ln(G+1) + bG2+cln²(G+1)](1+(Tc-To) =PM(G,25)(1+(Tc-To)
dove i parametri, a,b, c sono misurati per diversi valori di G e Tc=To mentre per  si
potrebbe utilizzare una singola misura ad una particolare temperatura Tc o il dato di
targa. Il modello è semplice in quanto richiede solo tre parametri, per le condizioni
STC.
Il modello Friesen/3/
È un ibrido dei precedenti modelli; MPP è definito da:
IM = Imo.G.[1+IM (Tc-To)]
VM =Vmo+C0.lnG +C1.ln2G+VM.(Tc-To)

IM e VM sono i coefficienti di corrente e temperatura in MPP nelle condizioni G=1
kW/m2 e To=25oC.
La potenza massima nelle condizioni (G,Tc) è:
PM(G,Tc)=IMVM= Imo.G [Vmo+C0.lnG +C1.ln2G+VM.(Tc-To)] .[1+IM (Tc-To)]
e nelle condizioni (G,To):
PM(G,To)=IMoG(VMo+C0lnG +C1ln2G)= PmoG+C0. IMo GlnG + C1IMo G ln2G
che richiede solo la determinazioni di C0 e C1 se si hanno i dati di targa di IMo, VMo,
IM, VM,.
Nelle condizioni operative si ha:
PM(G,Tc)=IMVM= [PM(G,2To) +VM. IMoG Tc-To)] .[1+IM.(Tc-To)]
E’ proposta anche l’espressione della temperatura della cella:
Tc=T+1,25.(NOST-20)G+Ta
con T ≈ 2oC sovratemperatura della cella rispetto al retro del modulo (NOST:
Nominal Operating Specific Temperature).
Ad es. per il modulo Sunpower STM210 F le misure hanno dato:
IMo=5,2 A; VMo= 39,5 V; IM=-1,21.10-4/oC; VM= -0,181V/oC; C0= -1,52V; C1= 1,57V e NOST = 42.7oC
La Tabella 5-III riassume le caratteristiche dei quattro metodi a cui si rimanda per il
calcolo delle espressioni della potenza massima
Espressione
diodo Heydenreich
Fries
en
si
si
PM(G,To)[1+(TcTo)]
PM(G,Tc)
si
si
Tabella 5-III Applicabilità die metodi di stima della potenza
Per valutare l’effetto della temperatura ambiente e della irradiazione G sul
funzionamento del modulo si è definito il parametro NOCT (Nominal Operating Cell
Temperature).
NOCT è la temperatura della cella più calda di un modulo a circuito aperto (cioè la
situazione termicamente peggiore) nelle condizioni normalizzate di G=0,800 kW/m2,
temperatura ambiente di 20 °C e velocità del vento di 1 m/s.
Per una generica condizione si ha:
Tc (G,Ta) = 1,25.(NOCT-20)G+Ta
Per cui si può calcolare la potenza massima PM(G,Ta) = PM(G,Tc) utilizzando la
precedente relazione.
3.Stima della resa energetica di un modulo
La produzione annua E(kWh/y) di un modulo è:
E(kWh/y) = hPm(h) h con 0<h<8760
con Pm(h) potenza oraria media misurata all’ora h (metodo diretto).
Questo metodo richiede la misura continua del punto di massima potenza (MPP).
Se si dispone di un modello della potenza massima PM(G,Ta) è sufficiente monitorare
lo stato delle condizioni ambientali più significative (G,Ta); stime più raffinate
possono tener conto anche della velocità del vento.
Sono stati proposti due metodi:
a) Il metodo indiretto o della serie temporale si basa sul modello (o stima) della
potenza
massima PM(G,Ta) funzione dello stato ambientale per cui:
E(kWh/y) =  h PM(G(h),Ta(h)) h
dove (G(h),Ta(h)) è lo stato ambientale all’ora h.
b) Il metodo statistico o delle matrici /4/ si basa sul numero medio statistico
N(G,Ta) degli eventi annuali di ogni stato ambientale (G,Ta):
E (kWh/y) =  GTa PM(G,Ta) N(G,Ta) = PM.N
Dove PM = PM(G,Ta) è la matrice che decodifica il modello e N = N(G,Ta) la
matrice degli eventi, da cui uno dei nomi del metodo.
Il metodo diretto ha il vantaggio di una misura esatta, ma richiede la disponibilità del
modulo e dello strumento di misura per l’intero periodo di misura; gli altri due
metodi richiedono il modello PM(G,Ta) della potenza disponibile.
Il metodo indiretto richiede la misura dello stato ambientale per l’intero periodo di
misura mentre il metodo statistico richiede la conoscenza statistica dello stato
ambientale.
In Fig. 5.10. si riporta un esempio del metodo delle matrici /4/: la matrice della
potenza massima PM(G,Ta), rilevata statisticamente, è filtrata dalle misure meno
significative per ottenere la matrice P’(G,Ta) per valori compresi ad es. fra 5 < Ta
(°C) < 40 e 50 < G (W/m2) < 1000
Per il calcolo del rendimento effettivo si richiede poi la misura o la stima l’energia
annuale dell’irradiazione solare:
H(kWh/anno.m2)=  h G(h) h
che corrisponde alle ore efficaci annuali; il rendimento effettivo è:
eff%= 100.E/(H.Am) dove Am è l’area efficace del modulo PV.
È molto utile disporre di una stima di prima approssimazione della potenzialità di
produzione dei moduli fotovoltaici in funzione della localizzazione, orientazione,
inclinazione, tipologia e tecnologia. Uno strumento informatico è il sito del Joint
Research Center (JRC): http://re.jrc.ec.europa.eu/pvgis/ che si basa su un GIS
(Geographical Information System) e da tutte le informazioni in funzione dei predetti
parametri.
4.Comportamento termico
La temperatura del modulo è determinante per la sua efficienza. Per valutarla si
definisce il modello termico del modulo fotovoltaico (Fig. 5.9a) dove:
- Pt è la potenza termica dissipata nel modulo;
- TAf è la temperatura ambiente alla superficie frontale (esposta al sole);
- TAr è la temperatura ambiente alla superficie posteriore ( retro; non esposta al sole);
- Rmf e Rmr sono le resistenze termiche del modulo verso la superficie frontale e
posteriore;
- RCf e RRf sono le resistenze termiche rispettivamente di convezione e radiazione
della superficie frontale;
- RCr e RRr sono le resistenze termiche rispettivamente di convezione e radiazione
della superficie posteriore;
- Tm è la temperatura media del modulo da determinare ( a rigore si dovrebbe
considerare la temperatura della cella termicamente più sollecitata).
Rmf e Rmr sono costituite a loro volta dalle resistenze degli strati di EVA e,
rispettivamente, del vetro frontale e del supporto (Teflar o altro) posteriore.
Tm è data dall’espressione, con l’analogia elettrica del modello termico (Fig. 5.8b):
Tm= Pt.RfRr/(Rf+ Rr) + TAr.Rf/(Rf+ Rr) + TAf.Rr/(Rf+ Rr)
dove: Rr=Rmr+ RCrRRr/(RCr+ RRr) e Rf=Rmf+ RCfRRf/(RCf+ RRf)
Per i calcoli ci si riferisce ad un modulo di 1m2 per cui Pt ≈ G (1-) se si tiene conto
anche della potenza dissipata dalla carpenteria che regge il modulo. La ventilazione
della superficie posteriore è la sola variabile su cui si può intervenire per limitare la
temperatura del modulo.
Esiste una semplice relazione, di prima approssimazione, fra la resistenza termica
complessiva e NOCT:
NOCT=(1-) RfRr/(Rf+ Rr)
5. Misure sui moduli
Le misure, necessarie alla certificazione, sono elettriche, meccaniche, termiche, ecc.
sono effettuate in laboratorio. Altre sono effettuate all’esterno anche sul luogo di
produzione (Fig.5.11).
Le misure in laboratorio prevedono:
1) la curva I-V con simulatore solare (Fig.5.8) seguendo le norme STC,
analogamente a quanto richiesto per le celle;
2) la temperatura della cella nelle condizioni prescritte per il parametro NOCT;
3) le prove di isolamento tra i terminali del modulo e la cornice oppure verso un
telaio di riferimento: la corrente di fuga non deve superare 50 A e la
resistenza di isolamento deve essere maggiore di 50 M. La tensione di prova
dipende dal tipo di modulo e sistema;
4) l’esposizione prolungata alla luce per moduli in silicio amorfo (norme CEI 8212) con irraggiamento di 800-1000 W/m2 fino a stabilizzazione della potenza
prodotta. La riduzione della resa non deve superare il 10%
Le misure all’esterno hanno come scopo:
1) la misura della produzione nelle condizioni atmosferiche (funzionamento in
campo) e della temperatura del modulo con rilevazione contemporanea
dell’irradiazione solare (con piranometro, possibilmente selettivo), della
temperatura ambiente, della velocità del vento e dell’umidità. Sono le misure
che permettono di valutare l’effettiva resa energetica di un modulo fotovoltaico;
2) la rilevazione di difetti visibili e di riduzione delle caratteristiche di isolamento
con prove di esposizione per un totale di 60 kWh/m2.
Esistono strumenti commerciali in grado determinare il punto di massima potenza
(Maximum Power Point, MPP) dotati anche di pacchetti software di elaborazione per
il calcolo dell’energia prodotta in un determinato periodo, sono gli inseguitori del
MPP chiamati Maximum Power Point Tracker (MPPT)
Per eseguire queste misure lo strumento deve essere dotato di un resistore, per
dissipare la potenza generata, e di un convertitore DC/DC per la determinazione di
MPP (ad es. MPPT3000, www.isaac.supsi.ch).
A causa della fondamentale influenza delle condizioni meteorologiche sulla
produzione fotovoltaica è molto utile poter confrontare la produzione di più moduli
fotovoltaici nello stesso istante e nella stessa localizzazione. A questo scopo si
possono usare tanti strumenti MPPT quanti sono i moduli da confrontare oppure
sistemi di comparazione per moduli fotovoltaici (Fig.5.11).
6 Ottimizzazione delle prestazioni del modulo
E’ essenziale che il modulo funzioni nel suo punto di massima potenza cioè su una
resistenza pari a (Fig. 1):
RM=VM/IM = R(VM)
Se la resistenza di carico è R ≠ RM si deve utilizzare un convertitore DC/DC che,
supposto ideale, ha rendimento energetico unitario ed è caratterizzabile dal solo
rapporto di trasformazione fra la tensione d’ingresso e quella d’uscita k=Vi/Vu=
Iu/Ii. Eguagliando le potenze nel punto di massima potenza si ha:
RuIuM2=PM=IM.V(IM) e semplificando
Iu = (PM / Ru)1/2 e kott=Iu/IM
Iu
I
V
DC/DC
k=V/Vu
Vu
Vu
Ru
M
P
P
T
2
2
V=k.Vu; I=Iu/k; R(V)= k2Ru; R(VM)= kM2Ru
ISC
IM
Iu
V2
R
I
PM
1
M
P
P
T
1
V1
Fig. 1
Per la ricerca di MPP si eguagliano le potenze per un generico valore di k:
RuIu2=I.V(I)
Il valore di I è ottenuto dall’equazione trascendente:
I =V(I)/Ru.k
con V(I)= VTo.ln(I/Isc+(1-I/Isc)exp(Voc/VTo).
Per trovare il punto di massima potenza basta a partire da ko=1 e massimizzare I(k) ad
esempio per successive approssimazioni.
Si pone k1= ko +k e si aumenta (o diminuisce) fino al massimo di I, per migliorare
l’approssimazione si cambia segno all’incremento e lo si dimezza in valore asoluto.
6.1 Moduli in serie
I moduli sono normalmente collegati in serie per avere la necessaria tensione
d’uscita, ma possono non funzionare nelle stesse condizioni (ad es. per
ombreggiamenti temporanei). Per evitare di ridurre eccessivamente le prestazioni è
stato proposto un metodo che collega ogni modulo ad un suo DC/DC (Fig. 6.11.b).
Si abbiano Q moduli in serie funzionanti ciascuno nel loro punto di massima potenza
(PiM=IiMViM, i=1÷Q), che i DC/DC siano tutti ideali e che alimentino un carico di
resistenza R percorso dalla corrente Iu. Si ha:
iPiM = RIu2
Da cui:
Iu =iPiM)/ R)1/2
e quindi i fattori di conversione valgono: kiM=Iu/IiM.
I fattori di trasformazione devono essere determinati dai rispettivi MPPT in modo da
massimizzare la corrente sul carico.
Data l’illuminazione di ogni modulo, R e specifici valori di ki, si ha:
RuIu2 =i IiV(Ii) = Iui IiV(Ii)/ki) e quindi Iu = = [i IiV(Ii)/ki]/Ru
da cui si ricava Iu .
Iterazioni
Si parte da valori iniziali di ki (ad es. ki=1); si incrementano successivamente i ki
calcolando ogni volta Iu; se questa aumenta si conferma il valore dell’incremento e si
passa al successivi ki. Altrimenti gli si cambia il segno e si calcola il nuovo solo
valore passando quindi al successivo ki. Si itera fino a raggiungere il massimo valore
di Iu.
7. Moduli a concentrazione
Questi moduli (Fig. 6.12b) concentrano la radiazione sulla cella per risparmiare
materiale semiconduttore, ma, in generale, hanno alcuni inconvenienti come la
necessità di raffreddamento e dell’inseguimento solare.
Il parametro distintivo dei moduli a concentrazione è il fattore di concentrazione. Si
hanno diversi modi di rappresentare la concentrazione:
- fattore di concentrazione solare (costante solare): kc (Fig. 2.a);
- fattore di concentrazione d’area: ka (Fig. 2.b));
- numero di soli; tiene conto dell’effettiva radiazione ad esempio tiene conto della
radiazione diffusa e dell’albedo.
I sistemi a concentrazione si suddividono in:
1) statici senza raffreddamento se ka<5;
2) statici con raffreddamento se ka< 20;
2) a inseguimento senza raffreddamento artificiale se ka<50;
3) a inseguimento con raffreddamento se ka>50.
In pratica non si supera il valore di ka=100.
T
dTS
a)
Radiazione incidente: G (kW/m2)
Area incidente: A

S
2RS
b)
Fig. 2
La costante solare si calcola eguagliando la potenza emessa dal sole (PS=Gs.4RS2) a
quella distribuita sull’area di una sfera avente per raggio la distanza terra-sole (dTS):
G.4dTS)2 = PS= Gs.RS)2
dove G è la radiazione sulla terra nella direzione dei raggi solari. La costante solare è
quindi:
kc=G/GS= (2RS/dTS)2/4= (sin)2 /4
Poiché  = 0,53° (Fig. 2.a) la costante solare è kc ≈ 4(1/)2 = 46.748 che rappresenta
il limite della concentrazione. Per il concentratore lineare (a grondaia) kc =1/(sin) e
il suo valore limite è kc ≈ (1/) = 218. In pratica questi valori devono essere scalati di
un fattore di almeno 4.
Il fattore di concentrazione d’area è ka=A/Am (A area della lente, Am area del
modulo). Con lenti convergenti il fattore di concentrazione dipende dall’indice di
rifrazione n della lente kan2 rappresentato dal rapporto di area ka (Fig. 6.13b).
7.1. Analisi del funzionamento del modulo a concentrazione
La maggiore irradiazione rispetto al caso di modulo senza concentrazione produce un
aumento di Isc, Voc e FF e quindi un aumento del rendimento.
Per una valutazione quantitativa di prima approssimazione si considera lo schema di
principio di un modulo (Fig. 6.13.c) con superficie captante dell’energia solare di
area A e con superficie delle celle fotovoltaiche di area Am. Se G è la radiazione sulla
superficie A la potenza Psc prodotta dal modulo senza concentrazione è:
Psc = Pu(G).A= (G) G.A
dove Pu(.) è la potenza per unità di superficie prodotta dal modulo.
La radiazione sul materiale attivo è G’= kaG e quindi la potenza Pcc prodotta dal
modulo a concentrazione è:

Pcc= Pu(G’)Am = Pu(kaG) Am = (kaG) G’ Am = (kaG) G A =(kaG)/ (G) .Psc
I vantaggi del modulo a concentrazione sono quindi:
a) un rendimento maggiore rispetto a quello di un modulo senza concentrazione,
anche se realizzato con lo stesso materiale;
b) area è ridotta di un fattore ka rispetto all’area captante;
c) convenienza ad usare materiali fotovoltaici più costosi se più efficienti.
Per contro si hanno alcuni svantaggi:
- un maggior riscaldamento delle celle;
- maggiori perdite per dissipazione elettrica;
- necessità d’inseguimento solare per alti valori dei fattori di concentrazione.
Esempio
Si considera un modulo costituito da Nc celle in serie e con le seguenti
caratteristiche:
Pmo Vmo
W
80
Imo Voco Isco 
V
A
V
A %/oC
17,2 4,65 21,6 5,28 -0,4
NOCT Nc
o
C
47
n.
celle
36
VTo
V
2,05
Da questo modulo si ipotizza di realizzare moduli a concentrazione con fattore di
concentrazione ka = 1÷36 e quindi con Nc’=Nc/ka. La radiazione prima della
concentrazione è G =200÷1200 W/m2 e la temperatura ambiente è Ta=10÷35oC.
Si suppone che esista un sistema di ventilazione o di raffreddamento che non
modifichi la temperatura della cella.
Per il calcolo della potenza disponibile si utilizza il modello ad un diodo.
Indicando con un apice (’) le grandezze del modulo a concentrazione si ha:
G’=G.ka; Isco’=Isco; Voco’= Voco/ka; VTo’=VTo/ka; ’= 
PM (G’,Tc) = IscoG’. [Voco’ + VTo’ ln(G’)] FF(G’,To)[1+’(Tc-To)]
e quindi con Voc= Voc(G,ka;To )= Voco+VToln(ka.G) la potenza disponibile è:
PCC= PM(G’,Tc) = PM(G,ka,Ta)= Isco.G.Voc FF(Voc)[1+g(Tc-To)]
G
Ta
Tc
1
W/m2 oC
oC
W
200
10 16,75 13,39
400
10
23,5 28,74
600
20 40,25 42,43
800
20
47 56,96
1000
25 58,75 69,40
1200
30
70,5 80,49
PM(G,Tc,ka)
4
12
18
36
W
W
W
W
16,13 18,33 19,15 20,56
34,12 38,44 40,04 42,80
49,99 56,06 58,32 62,19
66,79 74,67 77,60 82,62
81,08 90,44 93,91 99,88
93,76 104,40 108,35 115,12