finestra temporale della cosmic box – modalita

L’ESITO DI UN TEST DEL CHI QUADRO PER LA VERIFICA DI UN’IPOTESI
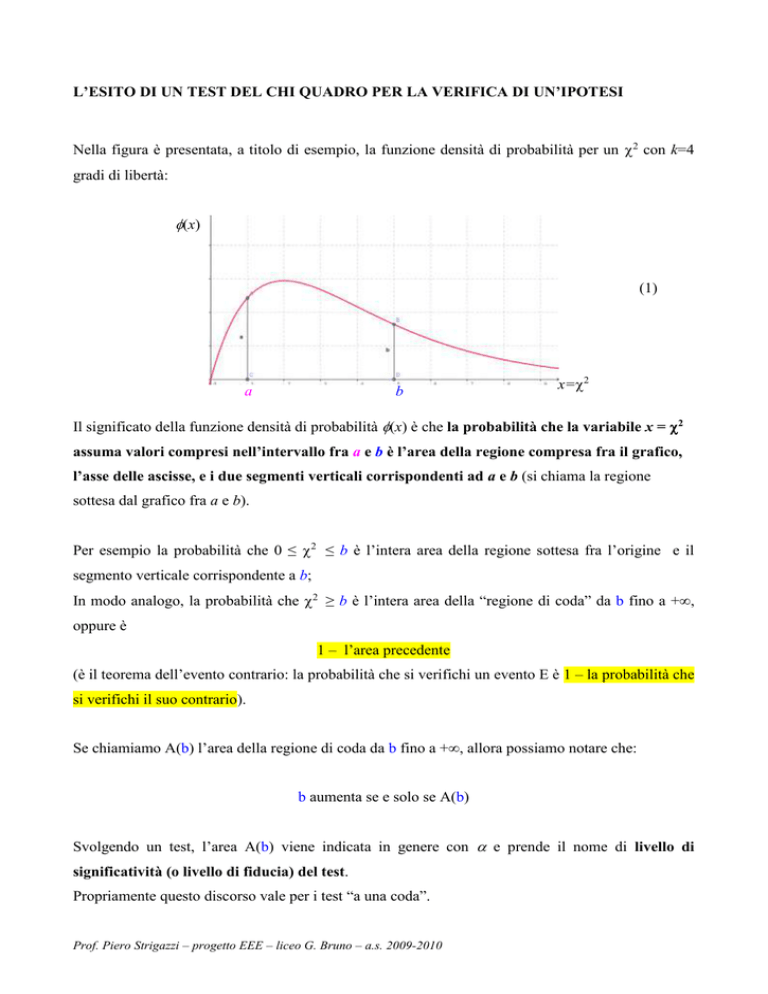
Nella figura è presentata, a titolo di esempio, la funzione densità di probabilità per un 2 con k=4
gradi di libertà:
(x)
(1)
a
b
x=2
Il significato della funzione densità di probabilità (x) è che la probabilità che la variabile x = 2
assuma valori compresi nell’intervallo fra a e b è l’area della regione compresa fra il grafico,
l’asse delle ascisse, e i due segmenti verticali corrispondenti ad a e b (si chiama la regione
sottesa dal grafico fra a e b).
Per esempio la probabilità che 0 ≤ 2 ≤ b è l’intera area della regione sottesa fra l’origine e il
segmento verticale corrispondente a b;
In modo analogo, la probabilità che 2 ≥ b è l’intera area della “regione di coda” da b fino a +∞,
oppure è
1 – l’area precedente
(è il teorema dell’evento contrario: la probabilità che si verifichi un evento E è 1 – la probabilità che
si verifichi il suo contrario).
Se chiamiamo A(b) l’area della regione di coda da b fino a +∞, allora possiamo notare che:
b aumenta se e solo se A(b)
Svolgendo un test, l’area A(b) viene indicata in genere con  e prende il nome di livello di
significatività (o livello di fiducia) del test.
Propriamente questo discorso vale per i test “a una coda”.
Prof. Piero Strigazzi – progetto EEE – liceo G. Bruno – a.s. 2009-2010
Il corrispondente valore b – che è un valore assunto dalla variabile 2 – è chiamato 2 critico (2crit)
relativamente al livello di significatività .
Il test di verifica di un’ipotesi (chiamata in genere “ipotesi nulla” e indicata con H0) consiste nel:
1) definire il livello di significatività del test (definire );
2) determinare il valore di 2crit; per questo scopo bisogna conoscere il numero di gradi di
libertà del 2 e poi usare le tabelle che vengono proposte;
3) calcolare, mediante i dati sperimentali, una quantità che sia corretto chiamare 2;
4) confrontare il calcolo ottenuto con il 2crit.
Qual è l’esito del test?
Il livello di significatività  per un test a una coda è la probabilità che i valori assunti dal 2 siano
maggiori o uguali a 2crit.
Dato che la quantità che viene calcolata mediante i dati sperimentali corrisponde a un modo per
indicare la dispersione degli stessi dati sperimentali rispetto ai valori teorici attesi, è ovvio che “il
miglior risultato” sembra essere 2 = 0, cioè non c’è nessuna dispersione: i dati sperimentali
coincidono sempre con quelli teorici.
Questo significa che l’esito di un test a una coda è positivo (cioè l’ipotesi nulla è da accettare),
se il 2 è minore del 2crit.
Poiché è poco probabile che situazioni del genere 2 = 0 possano accadere, se non perché i dati
sperimentali vengono artefatti, esiste la possibilità di svolgere il test “a due code”: la regione di
significatività non si trova più solo a destra, ma anche a sinistra (proprio come succede nel grafico
n.1).
2 crit sinistra
2 crit destra
Prof. Piero Strigazzi – progetto EEE – liceo G. Bruno – a.s. 2009-2010
Cioè la significatività del test è “suddivisa” fra valori troppo piccoli del 2 e valori troppo grandi del
2 : esistono due 2crit, uno a sinistra e uno a destra.
Questo significa che l’esito di un test a due code è positivo (cioè l’ipotesi nulla è da accettare),
se il 2 è compreso fra 2crit sinistrae2crit destra.
Nella tabella successiva ho riportato i valori critici presi dal testo del prof. Garfagnini, “Appunti alle
lezioni del corso di Esperimentazioni I B”, edizione 1993, CLU:
Prof. Piero Strigazzi – progetto EEE – liceo G. Bruno – a.s. 2009-2010
In questa tabella vengono presentati tre casi di :  = 0,10;  = 0,05;  = 0,01 per gradi di libertà
(DF) fino a 30.
Per ogni caso sono tabulati i valori del 2crit (a destra = limite a destra; a sinistra = limite a sinistra).
Alcune osservazioni:
1) il 2crit sinistra è sempre (ovviamente) minore del 2crit destra ….!
2) Il 2crit sinistra diminuisce diminuendo il livello di significatività , mentre il 2crit destra aumenta
diminuendo  (il confronto va fatto a DF costante): questo significa che la regione di
“accettazione” dell’ipotesi nulla, per cui 2 è compreso fra 2crit sinistrae2crit destra si allarga
diminuendo .
Questo significa che, aumentando il livello di significatività del test, è sempre meno
probabile che il valore calcolato del 2 possa essere al di fuori della regione di accettazione.
Quindi diminuire  significa rendere migliore l’esito del test
3) A qualunque livello di significatività e a qualunque numero di gradi di libertà, il valore del
2crit sinistraè sempre minore del numero di gradi di libertà, mentre il valore del2crit destra
è sempre maggiore del numero di gradi di libertà.
Questo è sensato, perché il numero di gradi di libertà è il valore più probabile del 2 (è il suo
valore medio!), quindi è plausibile che esso appartenga alla regione di accettazione!
4) Le tabelle riportano questi valori critici relativamente a “piccoli” : infatti se
considerassimo  = 0,8 vorrebbe dire che, in caso di esito positivo del test, la probabilità che
il 2 calcolato fosse al di fuori della regione di accettanza è 80%, quindi il fatto di avere
ottenuto quel risultato fa accettare l’ipotesi nulla con una sicurezza del 20%....
5) L’esito del test di verifica dell’ipotesi non è mai dato con certezza: l’ipotesi nulla viene
accettata (se l’esito è positivo) oppure rifiutata (se l’esito è negativo) a quel livello di
significatività che è stato considerato. Altrimenti detto, se l’ipotesi nulla viene scartata al
livello di significatività del 5%, c’è comunque la probabilità del 5% di aver scartato
un’affermazione vera!
Viceversa, se l’ipotesi nulla viene accettata al livello di significatività del 5%, c’è
comunque la probabilità del 5% di aver accettato un’affermazione falsa!
Prof. Piero Strigazzi – progetto EEE – liceo G. Bruno – a.s. 2009-2010