Soluzione es

RISOLUZIONE: Compito del 20 Luglio 2006
Reti in fibra ottica e Complementi di reti in fibra ottica
Soluzione es.1
C  1550nm
f  200GHz
RB = 10 Gbit/s
modulazione esterna
L = 60 Km
@ BER = 10-9
PSENS = -21 dBm
PTX = 2 dBm
 dB 
 Km 
 ( )  0.2  2.3  10 5 (  1550) 2 
 RX  4dB
2 D  1313nm
 CD  3
S  0.086
ps
nm  Km
2
L
LMAX
  3dB
BER  10 11
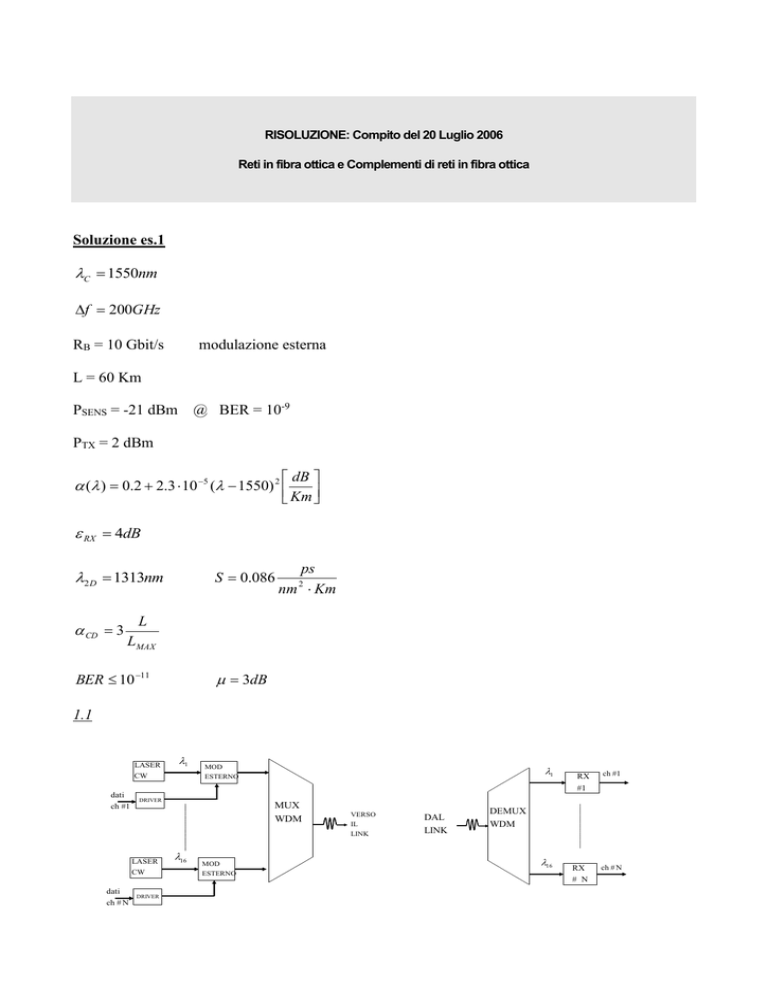
1.1
LASER
CW
dati
1
MOD
ESTERNO
DRIVER
1
MUX
WDM
ch #1
VERSO
IL
LINK
LASER
CW
dati
ch # N
DRIVER
16
MOD
ESTERNO
DAL
LINK
RX
#1
ch #1
RX
# N
ch # N
DEMUX
WDM
16
1.2
BER =
1
erfcPSENS 
2
Bisogna calcolare la sensitività a BER = 10-11, dato che non la si possiede e che la si può ottenere
conoscendo la sensitività a BER = 10-9  -25 dBm (valore fornito dall’esercizio).
 
 BER10
PSENS
PSENS
9

BER10 9
BER10
11

4.25
1
 535mW 
 2.1
10
 BER10

11

4.75
 8.9W  PSENS
535
BER101 1
 20.5dB m
1.3
Per il calcolo del numero di canali è opportuno valutare quale sia la lunghezza d’onda presente tra i
vari canali(essa si ottiene sapevo quanto vale, in frequenza, la spaziatura tra i vari canali)
PTX  Att    PSENS
f  200GHz 
  1.6nm
Att  PTX  PSENS  
Naturalmente nel calcolo interviene anche l’attenuazione introdotta dal filtro demultiplexer
 MAX L  PTX  PSENS     RX
 MAX 
2  20.5  4  3
 0.2583
60
 N  1 
2
0.2  2.3  10 5 
  (1.6)   0.2583
 2 

Alla fine, dopo le opportune sostituzioni si giunge a:
N 1
 31.47
2

N = 62
1.4
In questo caso invece bisogna prestare attenzione al fatto che deve essere considerata sia
l’attenuazione che la dispersione cromatica
 MAX L   CD  PTX  PSENS     RX
 MAX 
1
LMAX
1
 0.2583
LMAX
 10 DMAX  ( RB ) 2
E’ necessario notare che i canali sono centrati intorno a 1550 nm, mentre la fibra utilizzata ha uno
zero di dispersione situato alla lunghezza d’onda λNZ= 1313 nm.
DMAX  S  N  1313 


 N 1
 N 1
 0.0861550  
    1313  20.382  0.1376  

 2 
 2 


1
LMAX
 N 1
 0.0204  1.4  10 4  

 2 
 N 1
4  N  1 
0.2  5.9  10  
  0.0204  1.4  10  
  0.2583
 2 
 2 
2
5
 N 1
Pongo 
= X
 2 
5.9  10 5  X 2  1.4  10 4  X  0.0379
X 2  2.4  X  642.4  0
X 1, 2  1.2 
1.22  642.4  1.2  25.37 
 N 1

  24.17
 2 
N = 48
1)  26.57
2) 24.17
Soluzione es.3
Dati
RB = 40 Gbit/s
Nch = 32
f  100GHz
(PTX)TOT = 19 dBm 
PTX  19  10 log 10 (32)  3.95dBm
LTOT = 1200 Km
  0.3dB / Km
F = 6.5 dB
Bott = 100 GHz   = 2.5  OSNRpen = 1.7 dB
 = 2 dB
 PATH  2dB
3.1
BER  10-12  OSNRop  14.4 dB
Dato che il sistema è una sistema ottico multi-tratta, il corretto valore di OSNR sarà:
OSNR  OSNRop + OSNRpen + μ +  PATH
 OSNR  20.1 dB
A questo punto si utilizza la formula che esprime l’OSNR alla fine di una catena amplificata:
Psignal -  SPAN – 10 log10 NSPAN – FEDFA|dB – PBASE|dB  OSNR|dB
Si sostituiscono i parametri conosciuti:
PTX –  SPAN -10log(M) – F – PBASE  20.1 dB
3.95 – 0.3
1200
–10log(M) – 6.5 +52.9  20.1 dB
M
E otteniamo
36
+ log(M)  3.025 dB 
M
f ( M )  3.025
M
f(M)
20
3.1
21
3.03
22
2.97
 M = 22  LSPAN  54.5 Km
3.2
Si utilizza la formula che vale per D ≠ 0 delle sorgenti a spettro stretto:
D = 16
LMAX 
1
10  16  40  10 3 
2
 3.9 Km
Utilizzando una fibra con dispersione D = 16 ps/nm/km a 1550 nm, si ottiene una distanza massima
raggiungibile, inferiore rispetto a quella necessaria.
LMAX << LTOT  IL SISTEMA NON FUNZIONA
3.3
Il valore del compensatore deve portare a zero la dispersione accumulata su una tratta, dunque:
DCOMP = - LSPAN * D = - 54.5 * 16 = - 872
ps
nm
3.4
Non è ragionevole ipotizzare che sia trascurabile il valore della dispersion slope S in un sistema di
questo tipo, in quanto:
-il sistema è di tipo WDM e dunque occupa un intervallo di lunghezze d’onda ampio
-la lunghezza complessiva è molto elevata (1200 Km)