Dalla giunzione pn in silicio cristallino alla cella fotovoltaica
3.1.
Il silicio intrinseco
Il silicio non drogato (intrinseco) possiede elettroni e lacune nelle bande di conduzione e
rispettivamente di valenza; è utile calcolare le loro concentrazioni n0 e p0, rispettivamente:
n0= Ne(E)f(E)dE per E>Ec da cui n0 = NC.exp[-(Ec-EF)/kT]
p0= Nh(E)[1-f(E)]dE per E<Ev da cui p0 = NV.exp[-(EF-Ev)/kT]
dove:
Ne(E) (E-Ec)1/2 ,
Nh(E) (Ev-E)1/2
sono le densità volumetriche del numero dei possibili stati (livelli energetici) degli elettroni e delle
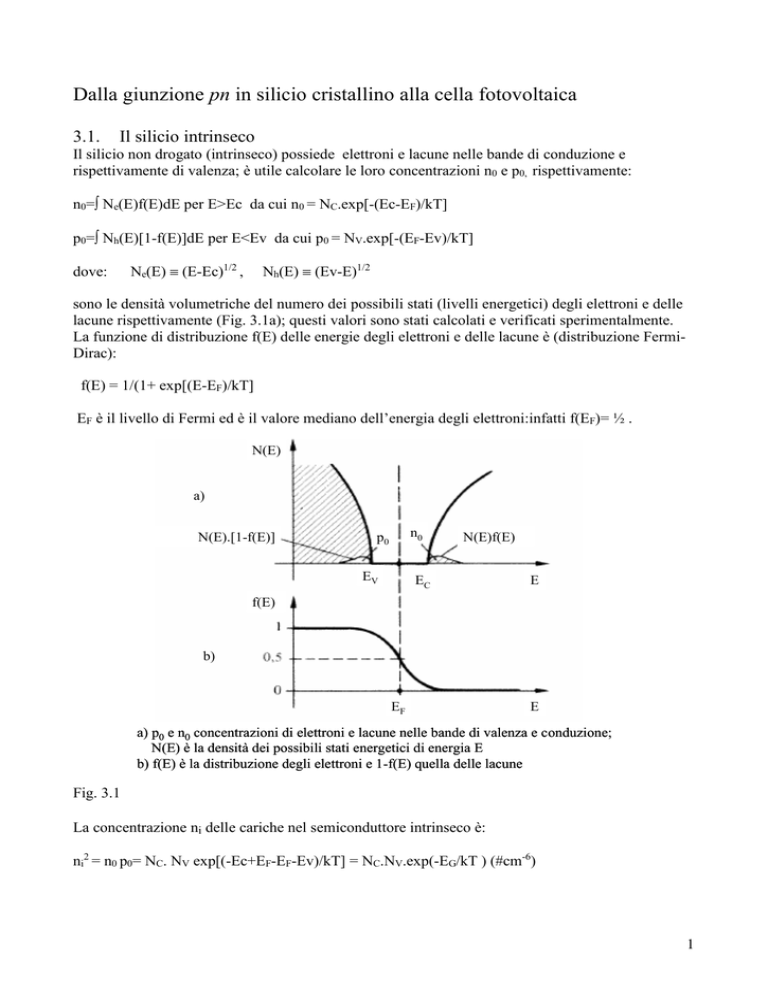
lacune rispettivamente (Fig. 3.1a); questi valori sono stati calcolati e verificati sperimentalmente.
La funzione di distribuzione f(E) delle energie degli elettroni e delle lacune è (distribuzione FermiDirac):
f(E) = 1/(1+ exp[(E-EF)/kT]
EF è il livello di Fermi ed è il valore mediano dell’energia degli elettroni:infatti f(EF)= ½ .
N(E)
a)
N(E).[1-f(E)]
n0
p0
EV
N(E)f(E)
EC
E
f(E)
b)
EF
E
a) p0 e n0 concentrazioni di elettroni e lacune nelle bande di valenza e conduzione;
N(E) è la densità dei possibili stati energetici di energia E
b) f(E) è la distribuzione degli elettroni e 1-f(E) quella delle lacune
Fig. 3.1
La concentrazione ni delle cariche nel semiconduttore intrinseco è:
ni2 = n0 p0= NC. NV exp[(-Ec+EF-EF-Ev)/kT] = NC.NV.exp(-EG/kT ) (#cm-6)
1
e dove NC e NV sono rispettivamente le densità degli stati nelle bande di conduzione e di
valenza e alla temperatura ambiente. Per il silicio NC ≈ 3.1019 (#cm-3) e NV ≈ 1019 (#cm-3);
per cui ni ≈ 1,5.1010 #cm-3 mentre la densità atomica è dell’ordine di N ≈ 1022 (#cm-3).
3.2.
Il silicio drogato
Il silicio, elemento del IV gruppo, (Tabella 3.I), ha caratteristiche intermedie fra quelle dei metalli
(conduttori di elettroni) e gli isolanti (non conduttori). Nei primi (vedi Fig. 2.1.) le bande di
valenza e di conduzione si sovrappongono, nei secondi sono talmente distanziate che è impossibile,
con valori non eccessivi di energia, spostare un elettrone dalla banda di valenza a quella di
conduzione.
Se nel cristallo di silicio si sostituiscono alcuni atomi con un elemento (impurità interstiziale) del V
gruppo (con un elettrone in eccesso nella banda di valenza, ad esempio fosforo , P) si ottiene il
silicio drogato n; se invece si sostituiscono alcuni atomi con un elemento del III gruppo (con un
elettrone in difetto nella banda di valenza, ad esempio boro, B) si ottiene il silicio drogato p.
Gruppo 1
Periodo
1
1
H
3
2
Li
11
3
Na
19
4
K
37
5
Rb
55
6
Cs
87
7
Fr
2
3
4
5
6
7
8
9
10 11 12 13 14 15 16 17 18
2
He
4
5 6 7 8 9 10
Be
B C N O F Ne
12
13 14 15 16 17 18
Mg
Al Si P S Cl Ar
20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36
Ca Sc Ti V Cr Mn Fe Co Ni Cu Zn Ga Ge As Se Br Kr
38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54
Sr Y Zr Nb Mo Tc Ru Rh Pd Ag Cd In Sn Sb Te I Xe
56 57 * 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86
Ba La Hf Ta W Re Os Ir Pt Au Hg Tl Pb Bi Po At Rn
88 89 * 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118
Ra Ac * Rf Db Sg Bh Hs Mt Ds Rg Uub Uut Uuq Uup Uuh Uus Uuo
58
Ce
90
** Attinidi
Th
* Lantanidi
59
Pr
91
Pa
60
Nd
92
U
61
Pm
93
Np
62
Sm
94
Pu
63 64
Eu Gd
95 96
Am Cm
65
Tb
97
Bk
66
Dy
98
Cf
67
Ho
99
Es
68
Er
100
Fm
69
Tm
101
Md
70
Yb
102
No
71
Lu
103
Lr
Tabella 3.I- Il sistema periodico degli elementi
Nel silicio drogato n, il numero degli elettroni nella banda di conduzione aumenta. Infatti l’energia
necessaria al salto di banda è minore di quella necessaria nel caso di semiconduttore intrinseco
(Fig.3.2.a) per cui la distribuzione di probabilità della loro energia si modifica e il livello di Fermi
(EFn) si avvicina a quello della banda di conduzione (vedi Fig. 3.2.b), l’opposto capita nel caso di
2
drogaggio p, in questo caso il livello di Fermi (EFp) si avvicina a quello della banda di valenza (vedi
Fig. 3.2.c).
i
Funzione di distribuzione dell’ energia degli elettroni per
un semiconduttore: intrinseco (i), drogato (n) e drogato (p)
Fig. 3.2
La funzione di distribuzione fi(E) (i n o p, rispettivamente per drogaggio n o p) nei materiali
drogati, è quindi:
fi(E) = 1/(1+ exp[(E-EFi)/kT] exp[(EFi -E)/kT ] per (E- EFi)/kT >>1.
Sia ND la concentrazione degli atomi droganti donatori e NA quella degli atomi droganti accettori; si
dimostra che l’ energia minima delle bande di conduzione e e quella massima delle bande di
valenza sono rispettivamente:
EC = EFn+kT. ln (NC/ND)
e
EV = EFp- kT.ln (NV/NA)
Al crescere di ND diminuisce la differenza EC-EFn e quindi aumenta la facilita di passaggio
di un elettrone alla banda di conduzione. Inoltre in ogni punto del silicio drogato le
concentrazioni n degli elettroni e quelle delle lacune p sono legate dalla relazione:
n.p=ni2
Per il silicio drogato n è n ≈ ND e per quello drogato p è p ≈ NA.
3.3.
Dalla giunzione pn alla cella fotovoltaica
La giunzione pn è costituita da una fetta di silicio (Fig. 3.3) suddivisa in una parte drogata n (zona
N) e l’altra drogata p (zona P) in cui si ha rispettivamente un esubero di cariche mobili (elettroni e
rispettivamente lacune). Le zone P ed N sono terminate da contatti metallici la cui polarità è
definita in base al tipo di funzionamento.
Le concentrazioni delle zone drogate producono anzitutto la diffusione delle cariche maggioritarie
di ogni zona: in tal modo rimangono, nelle corrispondenti zone, gli ioni dei droganti che
costituiscono la carica fissa. Questa crea un campo elettrico che arresta il processo di dislocazione
delle cariche mobili (in particolare gli elettroni).
3
Si raggiunge una situazione di equilibrio termodinamico in cui, per ogni tipo di carica, la diffusione
dovuta al gradiente di concentrazione delle cariche è compensato da un uguale flusso cariche per
deriva.
Drogante P ionizzato
Cariche fisse
Zona di svuotamento
(o d carica spaziale)
E
B–
ne
usio
– (diff
P
)
Drogante N ionizzato
Cariche fisse
P+
e
e – (deriva)
equilibrio
termodinamico
N
giunzione pn
Potenziale elettrico
La giunzione pn al silicio cristallino
Fig. 3.3
L’asimmetria della giunzione pn favorisce quindi lo spostamento degli elettroni dalla zona P alla
zona N (e viceversa per le lacune). Il campo elettrico E che arresta lo spostamento delle cariche in
una situazione di equilibrio termodinamico produce un potenziale elettrico 0.
Si esaminano le configurazioni tipiche (Fig. 3.4):
a) giunzione non polarizzata (Fig. 3.4a);
b) giunzione polarizzata direttamente (Fig. 3.4b);
c) giunzione illuminata ed alimentante un carico elettrico (Fig. 3.4c).
La cella fotovoltaica è un diodo pn al silicio, molto largo e sottile. Se la giunzione è illuminata il
campo E trasferisce elettroni e lacune, generate dai fotoni, dalla giunzione a un carico elettrico.
o
eo
P
a)
N
E
EF=EFn=EFp
EG
P
N
a1)
o
I
P
E N
e(o –V)
eV
b)
b1)
EFn
P
N
EG
V
EFp
o
e(o –V)
I
P
c)
E N
eV
c1)
Fig. 3.4
R
EFn
P
N
EG
EFp
V
Stuttura e livelli energetici della giunzione pn di una cella fotovoltaica
4
Giunzione non polarizzata (Fig.3.4a)
Questa configurazione può avere, indifferentemente, i contatti aperti o chiusi in quanto non si ha
alcuna generazione o assorbimento di potenza.
Sia EG la banda proibita del semiconduttore, EC e EV i livelli energetici di conduzione e di valenza,
NC e NV la densità degli stati di conduzione e di valenza; NA e ND le concentrazioni dei droganti,
EFn e EFp i livelli di Fermi nelle rispettive zone P e N.
Poiché la giunzione non è polarizzata (Fig. 3.4.a1) il livello di Fermi è costante in tutta la giunzione:
EF ≈ ½(Ec+Ev) = EFn= EFp:
e poiché EC - EFn= kT.ln(NC/ND) e
EFp- EV = kT.ln(NV/NA)
il potenziale elettrico 0 puo’ essere facilmente dedotto dalla Fig.3.4.a1:
e0 = EG-(EC-EFn)-(EFp-EV)= EG - kT.ln (NC/ND)- kT.ln (NV/NA)= EG - kT.ln (NCNV/NAND)
o anche 0= kT/e.ln(NA.ND/ni2) = VT.ln(NA.ND/ni2),
come ordine di grandezza è 0 ≈ 0,5÷ 0,9 V.
È possibile approssimare la distribuzione delle cariche elettriche con andamento rettangolare e la
transizione delle concentrazioni con uno scalino (modello a svuotamento) (Fig. 3.5); la giunzione è
costituita dalle zone:
-
di svuotamento (o di carica spaziale), di larghezza W, in cui le cariche elettriche (di
ionizzazione) sono dovute ai droganti polarizzati, ma carica totale nulla;
neutre con carica spaziale nulla e costituita dalle due parti della giunzione separate dalla
zona di svuotamento.
Zona di svuotamento
P
Q-+ Q+=0
N
Dati: EG, NA, ND,
eND
+
lp
ln
_
-eNA
0 =VTln(NAND/ni2)
0 =VTln(NAND/NCNV)+EG/e
0
Emax =
[(2e0)/(1/NA+1/ND)]1/2
E(x)
dE/dx=x
Q= eNDln= - eNAlp
0=(e/2(NAlp2+NDln2)
d/dx = - E(x)
(x)
0
W= lp+ln=
(2/e)0(1/NA+1/ND)
W
Fig. 3.5
lp
ln
5
Le equazioni dell’elettrostatica (date le concentrazioni NA e ND dei droganti) permettono di
calcolare le cariche di ionizzazione +/-Q e il campo elettrico Emax, che, integrato, dà il potenziale 0
delle dimensioni della zona di svuotamento (lp+ln=W) attorno alla transizione a scalino. Le
espressioni di calcolo sono riassunte in Fig. 3.5. e, in particolare, si ha:
0=(e/2)(NAlp2+NDln2)
Il modello a svuotamento è particolarmente utile per determinare le dimensioni della zona di
svuotamento. In particolare permette di affermare che le cariche maggioritarie al limite della zona
di svuotamento (o di transizione, giunzione fisica) hanno concentrazione:
nn0 ≈ ND e rispettivamente pp0 ≈ NA
ln(p); ln(n)
La Fig. 3.6.a rappresenta (in scala logaritmica e con le transizioni approssimate da segmenti di retta)
l’andamento della concentrazione n degli elettroni e delle lacune p in funzione della posizione nella
giunzione.
W
pp0
nn0
Giunzione:
a) non polarizzata
pn0
np0
ln(p); ln(n)
x
pp0
W
nn0
np0
pn1
np1
b) polarizzata direttamente
pn0
x
ln(p); ln(n)
Le
Fig. 3.6
pp0
Ln
W
Ge
nn0
Gn c) illuminata
pn0
x
np0
Le
Ln
Le cariche minoritarie, al limite della zona di svuotamento, hanno concentrazione:
pn0 ≈ ni2/ND = pp0exp(-0/VT) e rispettivamente np0 ≈ ni2/NA= nn0exp(-0/VT)
in quanto ni2/ NA.ND = exp(-0/VT)
6
Giunzione polarizzata direttamente (Fig.3.6.b)
La tensione V è applicata alla giunzione pn, con la polarità positiva al contatto della zona P, cioè
con verso opposto a 0: il suo effetto è una corrente nella giunzione dalla zona P alla zona N. La
valutazione di prima approssimazione ipotizza che la larghezza della zona di svuotamento non si
modifichi e che nella zona neutra la caduta di tensione e il campo elettrico siano entrambi nulli.
Siano pn1 e np1 le concentrazioni al limite della zona di transizione; i loro valori si ottengono
tenendo ponendo 0-V al posto del potenziale:
pn1 ≈ pp0exp(-(0-V)/VT) = pp0exp(-(0/VT) exp(V/VT) = pn0 exp(V/VT)
e rispettivamente
np1 ≈ np0exp(-(0-V)/VT) = np0exp(-(0/VT) exp(V/VT) = np0 exp(V/VT)
La polarizzazione modifica, in modo esponenziale, la concentrazione delle cariche minoritarie al
limite della zona di svuotamento, producendo un gradiente di concentrazione nella zona neutra che
produce la corrente nella giunzione.
Le cariche minoritarie nella zona neutra N si muovono, con l’ipotesi fatta, per diffusione e la
corrente all’ascissa x a partire dal limite della zona di svuotamento è:
Jh (x) = -eDh dp(x)/dx
Poiché la concentrazione delle cariche minoritarie è superiore a quella d’equilibrio si ha
ricombinazione. L’equazione di continuità per il flusso delle cariche minoritarie nella zona N è:
dJh(x)/dx = -e (pn(x)-pn0)/h = -e pn(x)/h
dove h è il tempo di vita delle lacune. Tenendo conto dell’espressione di Jh(x) si ha l’equazione
differenziale del II ordine:
Dh d2pn(x)/dx2= pn(x)/h
E definendo la lunghezza di diffusione Lh2=Dhh si ha:
d2pn(x)/dx2= pn(x)/Lh2
Integrando con le condizioni iniziali: p(0) = pn0exp(V/VT) e p()=pn0 e con V, la tensione applicata
alla giunzione pn, si ottiene:
pn(x)= pn0 + pn0[exp(V/VT)-1] exp(-x/Lh).
Analogamente per gli elettroni nella zona neutra P, dopo aver cambiato segno alla coordinata x, si
ha:
np(x)= np0 + np0[exp(V/VT)-1] exp(-x/Lh)
La corrente totale è ottenuta considerando i valori delle due correnti di diffusione ai bordi della zona
di svuotamento, nella quale è possibile trascurare la ricombinazione (W<< Lh e W<<Le):
J =Je(0)+Jh(0)= e(Denp0/Le+Dhpn0/Lh) [exp(V/VT)-1] =J0 [exp(V/VT)-1]
7
Jo è la densità di corrente di saturazione che dipende dal semiconduttore e dal drogaggio:
J0 = e ni2[De/(LeNA)+ Dh/(LhND)]
e un suo valore di prima approssimazione è:
Jo= 1,5 .108 exp(-EG/kT) mA/cm2
da cui segue che Jo diminuisce al crescere della banda proibita EG.
La giunzione illuminata (la cella fotovoltaica)(Fig.3.6.c)
Se la giunzione è illuminata e chiusa su un resistore di resistenza R l’energia dei fotoni libera
cariche elettriche che vengono separate, se si trovano nella zona in cui è efficace il potenziale , e
fornite al carico elettrico (Fig. 3.4c1). Si fa l’ipotesi, per un calcolo di prima approssimazione, che
la generazione delle coppie e-h avvenga uniformemente in tutto lo spessore della giunzione con un
flusso di G [#/(cm3.s)] (elettroni o lacune).
La concentrazione delle lacune nella zona N è data ancora dall’equazione di continuità, includendo
il contributo del flusso fotonico assorbito:
dJh(x)/dx = eG - e(pn(x)-pno),
ma la corrente vale:
Jh(x) = - eDh.dpn(x)/dx,
per cui:
Dh.d2pn(x)/dx2= pn(x)/h – G
da cui d2pn (x)/dx2 = pn(x)/Lh2 - G/Dh
Integrando con le condizioni iniziali: p(0) = pn0exp(V/VT) (V, in prima approssimazione, è anche
la tensione sul carico) e p() = Gh (la concentrazione delle cariche prodotte è proporzionale al
loro tempo di vita!), si ha:
pn(x)= pn0 + Gh+ [pn0(exp(V/VT)-1) - Gh] exp(-x/Lh)
e la corrente è:
Jh(x) = - eDhdpn(x)/dx = eDhpn0[exp(V/VT)-1]exp(-x/Lh)/Lh – eG.Lh exp(-x/Lh)
e quindi, al limite della zona di svuotamento:
Jh(0) = eDhpn0[exp(V/VT)-1]/Lh - eGLh
Analoghe espressioni valgono per la corrente prodotta dagli elettroni.
La Fig. 3.6.c rappresenta l’andamento delle concentrazioni nella giunzione illuminata in corto
circuito con le ipotesi semplificative fatte. In particolare è utile per la verifica del verso della
8
corrente: infatti le correnti di diffusione hanno verso opposto a quello della corrente della
giunzione polarizzata direttamente non illuminata (Fig. 3.6b).
Il funzionamento della giunzione illuminata, in corto circuito e in circuito aperto, è riassunto dalla
Fig. 3.7.
o
I
P
E N
eo
EFn = EFp
N
P
EG
a1)
b1)
o
I
P
E N
eVoc= o = EG
EFn
P
N
EFp
Voc
a2)
b2)
Giunzione fotovoltaica in corto circuito e a circuito aperto:
configurazioni (a) e andamento delle bande energetiche (b)
Fig. 3.7.
La corrente totale, come nel caso di polarizzazione diretta è:
J = Jh(0)- Je(0) = J0 [exp(V/VT)-1] – eG(Lh+Le)
Il secondo termine rappresenta la corrente fotovoltaica prodotta nella giunzione in corrispondenza
delle zone di carica spaziale quasi nulla. Si osservi che solo le zone a distanza inferiore alla
lunghezza di diffusione dalla zona di svuotamento sono efficaci per la generazione della corrente
elettrica. La zona efficace è costituita anche dalla zona di svuotamento, di larghezza W, per cui:
JL = e.G (Le+W+Lh) (mA/cm2)
In pratica la cella non lavora in corto circuito; la concentrazione ai bordi della zona di svuotamento
è funzione della tensione in uscita alla cella e quindi superiore ai valori intrinseci np0 e pn0
(ipotizzati sopra) ma la corrente ha sempre verso opposto a quello della giunzione non illuminata.
Riassumendo soltanto le cariche generate in un ristretto volume attorno alla superficie di contatto
delle zone drogate contribuiscono alla corrente effettivamente disponibile. In Fig. 3.8a è mostrata
la sezione trasversale di una cella le cui zone P e N hanno rispettivamente gli spessori Wp e Wn che
9
possono anche essere inferiori alle lunghezze di diffusione degli elettroni e delle lacune Le e Lh
rispettivamente.
superficie con possibilità di ricombinazione
a)
superficie con possibilità di ricombinazione
b)
Caratteristica I(V) della giunzione fotovoltaica con la convenzione degli
utilizzatori
Fig. 3.8
Se V è la tensione ai capi della giunzione illuminata, la corrente totale è la somma di JL (prodotta
dalla radiazione solare e comprensiva di tutte le perdite) di quella propria della giunzione Jpn (in
opposizione a JL) per cui (Fig. 3.9.b):
J= Jpn -JL -= Jo(exp(V/VT)-1)- JL
Il verso opposto fra JL e Jpn si giustifica con il fatto che il diodo costituito dalla giunzione (non
illuminata) e sottoposto alla tensione V, è un carico per il generatore di corrente fotovoltaica.
Dall’espressione di J [mA/cm2]si ricavano le relazioni dei parametri fondamentali della cella
fotovoltaica:
a) la corrente di corto circuito: Jsc= JL
b) la tensione a vuoto: Voc = VT ln(1+ JL/Jo) = VT ln(1+ Jsc/Jo)
la cui caratteristica j(V), con la convenzione dei generatori, è:
J= Jsc- Jo(exp(V/VT)-1) = Jsc[1-(exp(V/VT)-1)/(exp(Voc/VT)-1)]
La seconda espressione è particolarmente utile perché i suoi parametri, come si vedrà, possono
essere determinati con semplici misure.
10












