esercitazione

Corso di Laurea Specialistica in Biologia Sanitaria, Universita' di Padova
C.I. di Metodi statistici per la Biologia, Informatica e Laboratorio di Informatica (Mod. B)
Docente: Dr. Stefania Bortoluzzi
Materiale del corso: http://telethon.bio.unipd.it/bioinfo/Didattica_2006/HomeStatBioinfo.html
VI ESERCITAZIONE
Analisi di dati "caso-controllo" per l'associazione fenotipo-genotipo.
Metodi:
Programmi:
Tabelle di contingenza, test del chi quadro.
EXCEL e SPSS.
Gli studi “caso-controllo” sono uno dei principali strumenti per l’epidemiologia analitica. In uno
studio “caso-controllo” un gruppo di individui con una determinata patologia viene comparato con
un gruppo di individui sani per determinare quali specifici fattori possano causare la malattia. E’
auspicabile che tutti gli individui considerati facciano parte dalla medesima popolazione. Il sistema
“caso-controllo” permette ad esempio di investigare le relazioni tra il consumo di alcool e il cancro
alla faringe oppure tra il consumo di grassi saturi e il cancro al colon. Gli studi “caso-controllo”
sono particolarmente utili per studiare le cause di malattie rare in una specifica popolazione,
piuttosto che per studiare malattie comuni con molte cause.
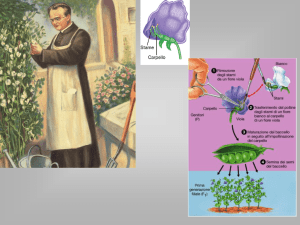
In questa esercitazione prenderemo in considerazione l’utilizzo di uno schema analitico di tipo
“caso-controllo” per lo studio dell’associazione tra un genotipo ed un fenotipo, in particolare tra un
polimorfismo del recettore alfa degli estrogeni (ER-) e il cancro al seno a Taiwan. La regione
genomica corrispondente al gene ER- e’ stata sequenziata in 189 pazienti ricoverate per cancro
alla mammella e 177 donne sane. E’ stato cosi’ evidenziato un sito polimorfo (SNPs), per il quale si
vuole verificare se le frequenze dei diversi alleli nel gruppo dei pazienti sono diverse da quelle nel
gruppo dei controlli sani. Il fine ultimo e’ quello di capire se la caratterizzazione di questo
polimorfismo del gene ER- possa avere un valore predittivo e/o prognostico riguardo allo sviluppo
del tumore.
DATI

190 donne con diagnosi di cancro alla mammella (eta’ media 46 anni)(casi);

177 donne sane (eta’ media 45 anni)(controlli);

in totale, 734 sequenze delle regioni trascritte del gene ER-;

dati riguardanti la storia familiare di 180 casi.
1
Scaricare il file di excel con la tabella originale contenente i dati sperimentali;
GENOTIPI
ER-Alpha
00
01
11
Exon 1, codon 10
(TCT->TCC)
TCT/TCT
TCT/TCC
TCC/TCC
CASI
95
77
18
CONTROLLI
69
73
35
CASI con storia
familiare
12
1
4
CASI senza storia
familiare
76
70
17
Utilizzando Excel:
2
Calcolare i totali per i casi, i controlli e gli alleli;
3
Calcolare le numerosita’ dei due alleli:
ad es. N(0) = n(00)*2 + n(01)
ottenendo una tabella di contingenza dei valori osservati:
Casi
Allele 1
Allele 0
N1 casi
N0 casi
Controlli N1 contr.
4
N0 contr.
Calcolare i totali marginali della tabella secondo lo schema seguente:
Allele 1
Allele 0
Totali
N1 casi
N0 casi
Ncasi = N0 casi + N1 casi
Controlli N1 contr.
N0 contr.
Ncontr = N1 contr. + N0 contr.
Totali
N0
N0 + N1 o Ncasi + Ncontr
Casi
N1
Ovvero:
Allele 1
Allele 0
Totali
Casi
A
B
AB
Controlli
C
D
CD
Totali
AC
BD
ABCD
5
Display grafico dei dati con un istogramma.
6
Interpretazione descrittiva dei risultati. Le frequenze alleliche dei casi e dei controlli
sono diverse ?
7
Calcolare la tabella dei valori attesi nell’ipotesi di indipendenza, utilizzando i totali
marginali:
Allele 1
Allele 0
Totali
= AC *AB / ABCD
= BD * AB / ABCD
AB
Controlli = AC *CD / ABCD
= BD * CD / ABCD
CD
BD
ABCD
Casi
Totali
AC
8
Per stabilire se le variabili sono indipendenti, cioè se i profili di riga (ovvero i profili di
colonna) sono tutti simili fra loro è possibile utilizzare il test del chi quadrato di
indipendenza.
9
Preparare il file per SPSS. I dati sono di tipo categoriale, definire le categorie
casi/controlli e allele 1/allele 0 con i valori numerici 1 e 2 (ad esempio A = casi/allele 1
 1/1, C = controlli/allele 1  2/1).
10
Copiare ed incollare i dati in SPSS.
Utilizzando SPSS:
11
Eseguire l’analisi descrittiva per tavole di contingenza selezionando il test del chi
quadrato e il coefficiente di contingenza. Calcolare anche frequenze e percentuali.
12
Interpretare i risultati tentando di rispondere alle seguenti domande:
-
Quali sono le deviazioni osservate ?
-
L’ipotesi di indipendenza viene confermata o rigettata ( = 0.05)?
-
Quale e’ la significativita’ del dato ?
13
Ripetere l’analisi (dal punto 3 al punto 13) per la classificazione “casi con storia
familiare” e “casi senza storia familiare”.
14
CONSEGNARE UNA RELAZIONE CONTENENTE:
-
Riassunto dei contenuti dell’esercitazione (massimo 150 parole).
-
Risposte ai punti in grassetto.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
VADEMECUM
La metodologia delle tabelle di contingenza e’ una tecnica semplice per esaminare relazioni tra
variabili categoriali (nominali o ordinali).
Questa procedura permette di testare l’indipendenza tra le variabili e di misurare l’entita’ di
eventuali associazioni osservate, nonche’ della affidabilita’ dei dati presi nel loro complesso.
Il test del chi quadrato su una tabella di contingenza misura la discrepanza tra i conteggi di cella
osservati e quelli attesi quando righe e colonne non siano correlate (ipotesi di indipendenza). Questo
test restituisce la probabilita’ di osservare per caso valori uguali o piu’ estremi di quelli
dell’esperimento, se le variabili prese in considerazione non sono correlate.
Il test del chi quadrato permette solo di escludere oppure ipotizzare una relazione di dipendenza,
percio’ sono state sviluppate altre misure (Symmetric measures) per quantificare l’affidabilita’ delle
relazioni osservate attraverso indici di associazione.
Contingency coefficient:
C
2
N  2