1)Introduzione

INDICE :
1-Introduzione………………………………………………………………...pag 2
Schema della presentazione…………………………………………………...pag 2
2-Il problema CP forte:
2.1-Il termine θ…………………………………………………………......pag 3
2.2-I settori θ……………………………………………………………….pag 5
2.3-I limiti su θ…………………………………………………………… .pag 7
3-Può la QCD risolvere il problema CP stesso?................................................pag 9
4-La ricerca di soluzioni oltre QCD: il meccanismo di Peccei-Quinn…….....pag 12
5-Gli Assioni:
5.1-Breve rassegna sui modelli assionici…………………………………...pag 14
5.2-Restrizioni sulla massa dell’assione……………………………………pag 15
6-Esperimento PVLAS(Polarizzazione del Vuoto con LASer):
6.1-Motivazioni……………………………………………………………..pag 16
6.2-Accoppiamento degli assioni con il campo elettromagnetico e effetti su un
raggio laser……………………………………………………………………pag 18
6.3-Apparato e risultati……………………………………………………...pag 24
7-Commento dei risultati da PVLAS e conclusioni…………………………..pag 27
8-Bibliografia………………………………………………………………....pag 29
1
1-INTRODUZIONE:
Sono trascorsi almeno trenta anni da quando l’assione fu introdotto nella fisica delle
particelle,come possibile soluzione del problema C P forte. Mentre all’origine la
fisica dell’assione era considerata in modo predominante entro un contesto della
cromodinamica quantistica (QCD),attualmente l’attenzione si è concentrata
sull’astrofisica. Ben presto si è realizzato che l’assione poteva essere un candidato
interessante per la materia oscura sia galattica(alone) sia extragalattica(cosmologica).
Allo stesso tempo,dopo un rapido sviluppo negli anni ottanta,i teorici della QCD
hanno perso interesse verso questo argomento. La ragione è ovvia:il progresso nel
comprendere la struttura del vuoto della QDC era piuttosto lento e l’impressione
prevalente era che “niente altro dovesse accadere”.
Il nostro scopo è quello di argomentare quanto vi sia di interessante nella struttura
complicata del vuoto,obiettivo sostenuto dall’esperimento PVLAS sulla birifrangenza
del vuoto,fenomeno che richiederebbe gli assioni per una spiegazione teorica.
Da non dimenticare il sostanziale progresso che è stato raggiunto in anni
recenti,ottenuto principalmente dalla supersimmetria e dalla teoria delle brane che
sancisce come fondamentale l’esistenza dell’assione.
Cominciamo con il comprendere le motivazioni e la necessità della sua introduzione,
per poi concentrarci sui dettagli dell’esperimento.
SCHEMA DELLA PRESENTAZIONE:
Cap 2: Viene introdotto il problema da risolvere, quello dell’osservazione
sperimentale della simmetria CP nelle interazioni forti, non riscontrabile teoricamente
nella Lagrangiana della QCD che presenta un termine della forma E·B, il cui
coefficiente di proporzionalità è detto angolo di vuoto θ. Si discute come questo
termine non possa essere reso automaticamente nullo. Si presenta come conseguenza
un contributo al momento di dipolo elettrico del neutrone, sperimentalmente vicino
allo zero: questo comporta limitazioni rigide sul valore di θ che deve essere, pertanto,
nullo o comunque molto piccolo.
Cap 3: Si prova a ricercare un meccanismo che forzi dinamicamente il valore di θ a
zero, operando sempre nell’ambito della QCD, cioè senza invocare nuova fisica. Si
percorrono diverse strade: l’effetto dello schermo di colore o una trasformazione
chirale valida presupponendo che la massa di almeno un quark sia nulla,ma ognuna di
queste soluzioni risulta insoddisfacente se non inconsistente.
Cap 4:Dai risultati del capitolo precedente si arriva alla necessità di un nuovo
meccanismo; la prima possibilità è quella introdotta da Peccei [n] e Quinn che hanno
ipotizzato la presenza nella Lagrangiana del modello Standard di una simmetria
globale chirale che viene spontaneamente rotta. Questo prevede l’esistenza di un
nuovo (pseudo)bosone di Goldstone che permette di far rilassare θ a zero.
Cap 5:Viene presentato sommariamente il primo modello assionico, quello di
Weingberg e Wilczek, in cui la scala di rottura della simmetria di Peccei-Quinn è
2
ancora legata a quella elettrodebole, cosa che risulta inconsistente con i dati
sperimentali. Si passa poi ai due modelli accettati, quello KSVZ e quello ZDFS, in
cui le due rotture(della simmetria di PQ e elettrodebole) vengono separate e
avvengono a scale energetiche diverse: si basano entrambi sulla stessa simmetria di
PQ ma l’assione viene introdotto con modalità diverse, comportando delle differenze,
anche se non enormi, tra i due valori della massa e della costante di accoppiamento
dell’assione, che descrivono completamente tale particella. Nella seconda parte
vengono riportati i limiti nella massa dell’assione da considerazioni astrofisiche.
Cap 6:Seguendo il lavoro di Maiani,Petronzio e Zavattini viene presentato il processo
di accoppiamento del campo assionico a due fotoni(processo Primakoff). Si
considera in particolare il caso di raggi laser polarizzati linearmente in presenza di un
campo magnetico esterno costante. Si descrive il cambio di polarizzazione del
raggio,che diviene polarizzato ellitticamente,valutando l’ellitticità e e l’angolo α(L)
che il semiasse maggiore dell’ellisse forma con la direzione del campo magnetico.
Con le basi teoriche necessarie, sviluppate particolarmente nella sessione 6.2, si
affronta la descrizione delle motivazioni all’origine delle ricerche dell’esperimento
PVLAS:si descrive l’apparato e si riportano i risultati.
Cap 7:Si commentano i risultati dell’esperimento PVLAS(Polarizzazione del Vuoto
con LASer)confrontando i limiti ricavati sulla massa e sulla costante di
accoppiamento dell’assione con i risultati emersi da altri esperimenti.
Si conclude presentando le ricerche future per far luce ulteriore sul problema.
2-IL PROBLEMA CP FORTE:
2.1-IL TERMINE θ:
Dopo la scoperta della libertà asintotica in QCD nel 1973,per breve tempo si credette
che la QCD avesse le stesse “scontate” leggi di conservazione del suo più semplice
predecessore,la QED: proprio per questo motivo la scoperta che in essa la
conservazione P e T non è naturale fu una sorpresa shockante. Procediamo per
gradi:è da riconoscere che uno dei principali vantaggi della teoria di colore di gauge
delle interazioni forti è che molte delle simmetrie osservate (P,T,C e conservazione
del sapore) sembrano seguire automaticamente come conseguenza del principio di
gauge e della rinormalizzabilità . Come conseguenza di ciò le teorie di gauge delle
interazioni deboli e forti si mescolano esattamente e effetti come violazione di parità
e processi con cambiamento di sapore si calcolano essere fortunatamente piccoli,e gli
effetti di rinormalizzazione potenzialmente dannosi sembrano essere sotto controllo.
Questo quadro della situazione piuttosto allettante è,comunque,basato sull’aver
trascurato tutte le possibili interazioni della forma:
Lθ = θ
G aμν G̃
32 π2
a
μν
= θ Tr(GμνG̃ μν ) ~Ea·Ba con a=1…..dimGruppo
32 π2
Dove Gμν è il tensore di forza e G̃ μν il suo duale, scritti nella forma di matrici,
G̃ aμν=(1/2)εμναβGaαβ mentre E e B sono campi cromodinamici(anche se un termine del
genere è possibile porlo per la QED:in questo caso i due campi corrisponderanno a
3
quello elettrico e magnetico. Come vedremo, la possibilità di definire un termine di
accoppiamento di questa forma tra il campo dell’assione e quello elettromagnetico è
alla base dell’esperimento PVLAS).
L’ operatore GG̃ ha dimensione quattro e può essere aggiunto alla Lagrangiana
della QCD,alterandone la simmetria. Riconoscendo infatti la sua struttura,della forma
E ·B e tenendo conto che per
C (coniugazione di carica): E
-E
P (inversione spaziale o parità): E
T (inversione temporale): E
B
-E
+E
B
-B
B
+B
-B
Allora questa interazione rompe P e T ma conserva C. Conoscendo il teorema CPT
secondo cui,se la teoria è locale e Poincarè invariante (cioè invariante per
trasformazioni del gruppo lineare non omogeneo di Lorentz, detto di Poincarè) le
leggi della fisica sono invarianti per simmetria CPT, allora una violazione della
simmetria T deve essere compensata da una violazione della simmetria CP,
fenomeno non riscontrato sperimentalmente. E’ infatti noto che le interazioni forti
conservano CP, da cui deriva che un problema naturale è quello di stabilire i limiti
sperimentali sul parametro θ che fissa l’entità dell’interazione, chiamato ANGOLO
DI VUOTO, con un valore compreso tra 0 e 2π. Il problema da risolvere è quello che
riguarda il perché il valore di θ debba essere naturalmente piccolo (i limiti derivano
dalle conseguenze problematiche che introdurrebbe nella teoria, tra cui un valore non
nullo del momento di dipolo elettrico del neutrone,come vedremo): questo è il
problema CP forte.
Viene però spontaneo chiedersi:questo termine problematico che è stato introdotto a
priori nella Lagrangiana della QCD potrebbe essere una inutile complicazione, in
quanto il suo contributo all’ azione e quindi alle equazioni del moto potrebbe essere
nullo. Ovvero,prima di trovare una possibile soluzione al problema CP bisogna
analizzare in maniera più approfondita la natura del termine incriminato, in quanto
potremmo trovarci anche nella fortuita situazione in cui si sta cercando di risolvere un
problema che in realtà non esiste, ma che è sorto da una errata analisi. Questo non è il
nostro caso, infatti la comprensione degli effetti non perturbativi indotti dai cosiddetti
istantoni ha dimostrato che il θ termine, Lθ , è non nullo necessariamente. Vediamo il
perché.
Il termine θ può essere riscritto come
Lθ= θ∂μKμ dove Kμ è la CORRENTE DI CHERN-SIMONS definita come
Kμ = (1/16) εμνρσ Tr(Aν∂ρAσ + (2i/3) AνAρAσ)
4
Sfruttando le regole di commutazione secondo cui [Aμ,Aν]=ifabcAbμAcνTa con fabc
l’insieme delle costanti di struttura del gruppo, si può riscrivere K μ in modo
alternativo anche come Kμ =(1/(16π2)) εμναβ(Aaν∂αAaβ-(1/3)fabcAaνAbαAcβ)
La ridefinizione del θ termine in funzione di questa nuova corrente non è stato un
semplice esercizio fine a se stesso, poiché avendo scritto L θ come una derivata totale,
si potrebbe concludere che la sua azione, cioè l’integrale quadridimensionale di L θ, è
nullo e pertanto non influenza le equazioni del moto. Questo è però un risultato
ottenuto ad un livello ingenuo, presupponendo che i campi vadano piuttosto
rapidamente a zero all’infinito. Al contrario, gli istantoni hanno rivelato che la
struttura del vuoto in QCD è più complicata di quella in QED. Per istantoni si
intendono le soluzioni classiche localizzate, ad azione finita della versione euclidea
delle equazioni di campo di un certo modello: consiste nella cosiddetta
approssimazione semiclassica, non perturbabativa, dove affinché il contributo
all’integrale di cammino “Lagrangiano” ∫Dx│x(tf) exp((i2πS[x(t)])/h) sia non nullo,
x(ti)
deve avere,appunto, azione finita.
In particolare, nel nostro caso, le configurazioni di campo con condizioni al contorno
istantoniche danno origine ad un integrale non nullo
(∆Sθ)un istantone=∫d4x(Lθ)un istantone≠0
Da questo si ricava che gli effetti di violazione CP possono essere presenti nelle
interazioni forti. Bisogna soffermarci per fare una nota esplicativa della espressione
precedente;per questa motivazione una nozione chiave è rappresentata dalla carica
topologica Q di una configurazione di campo di gauge
Q=∫d4x∂μKμ=∫d3xK0(x,t) │t=+∞ = K (t=+∞)- K(t=-∞) (1) (K0 è la componente
t=-∞
normale al bordo)
Dove di solito ci si riferisce a K con il nome di numero di Pontryagin.La carica
topologica è nulla per campi di gauge perturbativi,che sono quindi detti avere una
topologia triviale. Al contrario la configurazione di campo istantonico, come in
questo caso, non ha una topologia triviale, infatti Q è non nullo, anzi in una pura
gauge per cui Aμ=UDμU+ con U=exp(iαaTa) Q è un numero relativo(Q Є Z).Proprio
per questo fine è stato scelto il coefficiente di normalizzazione (1/32π2) davanti a Lθ,
affinché il valore di Q sia un valore intero, cioè assuma valori discreti(carica
topologica multipla di una fondamentale, presa unitaria).
2.2 I SETTORI θ:
Come si è rimarcato nella precedente sessione,il valore del parametro θ può essere a
priori arbitrario:le teorie con differenti valori di θ e quindi dello stato di vuoto QCD
|θ› descrivono differenti mondi che non “comunicano” l’un l’altro. Si dice che i
mondi con differenti |θ› appartengono a diversi settori di superselezione. Per
comprendere meglio ciò e soprattutto per esplicitare il ruolo di θ nello stato di
vuoto,consideriamo la pura gluodinamica nella gauge di Hamilton A0=0 in cui la
5
Lagrangiana non dipende da A0. Questo vincolo di gauge non elimina, comunque, la
libertà, infatti sono ancora permesse trasformazioni puramente spaziali di gauge
( indipendenti dalla variabile tempo),il cui generatore può essere scritto come
G(α)=exp(i ∫d3xTrDiGi0(x)α(x) dove la traccia scorre sugli indici di colore. Tale
generatore G (α) agisce sulle componenti spaziali dei campi di gauge e si può
mostrare che tale operatore non commuta con l’operatore di carica topologica Q se le
corrispondenti trasformazioni di gauge danno origine a un valore non nullo nel lato
destro dell’equazione (1): queste ultime sono chiamate “grandi trasformazioni di
gauge”.
[G,Q] ≠0
Siccome non commutano,questo vuol dire che non possono avere una classe di
autostati comuni e pertanto un autostato di Q non può essere uno stato fisico.In
realtà,lo stato fisico è definito come una sovrapposizione degli autostati di Q :
|θ› = ∑+∞ einθ|n› dove Q|n›=n|n› .
n=-∞
Per trovare una spiegazione semplice e intuitiva, tutto questo è analogo a ciò che
succede in un solido in cui, data la struttura cristallografica con atomi in locazioni
fissate da un passo reticolare,non esiste per il sistema una simmetria continua ma
discreta, cioè [H,P] ≠0 dove P è l’operatore impulso. E’ possibile invece definire un
operatore Ta che definisce il passaggio da un sito ad un altro, Ta| n›=| n+1› e
Ta-1=| n-1› per cui [H, Ta]=0. E’possibile perciò,definire lo stato fisico di vuoto come
una combinazione lineare degli stati |n›(che mi definisce il sito n-simo) in modo che
sia un autostato sia di H che di Ta : H|θ›=E|θ› e Ta|θ›=e-iθ|θ›
Infatti dato |θ›=∑neinθ|n› allora
Ta|θ›=Ta (∑neinθ|n›)=∑n einθ Ta |n›=∑n ei(n+1-1)θ |n+1›= e
-iθ
|θ›
Ritornando al discorso QCD, nello spazio dei campi infinito dimensionale c’è una
direzione parametrizzata dalla variabile K= ∫d3x K0 che forma un cerchio chiuso.
La funzione d’onda(come funzione di K) è appunto una sovrapposizione di
Bloch(come nel caso dell’analoga sua teoria dei solidi). Il parametro θ è chiamato,
proprio per questo motivo, definendo lo stato di vuoto, l’angolo di vuoto.
In questa formulazione θ entra come una fase arbitraria e varia in un intervallo da 0 a
2π: la fisica deve essere periodica in 2π, cioè l’azione di Lθ con θ sostituito da θ+2π
non deve dare un risultato diverso. Si può mostare, inoltre, che per ogni generico
operatore  che sia gauge invariante vale la condizione ‹ θ’| |θ ›~δθ’θ da cui si ricava
che non esiste nessun operatore che possa trasformare uno stato di un mondo definito
da un θ in un altro stato di un secondo mondo, definito da un altro θ; pertanto i
differenti mondi θ sono disconnessi l’un l’altro, cioè non collegabili topologicamente
per archi.
6
2.3 LIMITI SU θ :
Prima di avventurarci a discutere i limiti sperimentali di θ bisogna non trascurare che
in una teoria completa,con i quarks,c’è un termine addizionale alla parte di
Lagrangiana CP dispari,che si origina dalle fasi immaginarie della matrice M di
massa dei quarks. Queste fasi possono essere eliminate dalla matrice di massa tramite
una trasformazione chirale dei campi dei quarks. Infatti, scrivendo una Lagrangiana
nella forma
L=L+=MψRγ0ψL+M*ψLγ0ψR dove L sta per levogiro, R per destrogiro e M è la
matrice di massa (γ5ψL =-ψL e γ5ψR=+ ψR dove γ5=i γ0γ1γ2γ3 ).
Sommando sui sapori(f sta per flavour) L=∑f (MfψRfγ0ψLf+Mf*ψLfγ0ψRf).
Tramite la trasformazione chirale ψ’L=exp(-iαL)ψL e ψ’R=exp(-iαR)ψR per cui
L’=∑Mf exp(i(αL-αR))ψRfγ0ψLf +M*fexp(i(αR-αL)ψLfγ0ψRf
Siccome Mf=|Mf|exp(iαfM) con αfM l’insieme delle fasi degli autovalori della matrice
M, scegliendo αL- αR= - αM allora si cancellano queste fasi. Comunque, a causa della
anomalia assiale, che si manifesta come una non invarianza della misura
dell’integrale di Feynman sotto le trasformazioni chirali, tali fasi appaiono davanti al
termine GG̃ nella Lagrangiana QCD come ∑fαfM. Siccome è possibile diagonalizzare
la matrice M come
M1
M=
…..
MNf
|M1|exp(iα1M)
=
…………
|MNf|exp(iαNM)
Allora il determinante è detM=∏f|M|exp(i∑f αfM ). Pertanto ∑fαfM = arg (detM).Ne
consegue che il parametro definitivo e completo che stabilisce l’ampiezza della
violazione CP in QCD è dato da θ̃=θ+arg(detM), ma, per semplicità di notazione,
nella successiva discussione si denoterà con la stessa lettera θ
il θ̃.
Il problema CP, come abbiamo già evidenziato , sorge dal bisogno di spiegare il
perché la natura scelga un valore incredibilmente piccolo di θ, invece che dell’ordine
dell’unità; la speciale scelta di θ deve essere veramente vicina a zero: questo è un
caso di un enorme aggiustamento estremamente preciso in fisica(“fine tuning”).
La necessità di un θ piccolo sorge dal fatto che il più pronunciato effetto di questo
termine è la generazione di un valore non nullo per il momento di dipolo elettrico del
neutrone(nEDM).
7
.
n
π–
in
in
p+
γ
n
Prima di tutto bisogna far notare che non è un qualcosa di fantascientifico il porre che un oggetto neutro
come il neutrone abbia un momento di dipolo
elettrico, poiché, in quanto particella non elementare,
può avere un comportamento simile alle molecole di
sostanze come l’acqua che, seppur globalmente
neutre, presentano un momento di dipolo permanente
per la particolare natura del legame atomico. Processo
analogo può verificarsi nel caso del neutrone per
fenomeni spontanei quali ad esempio la dissociazione virtuale(non può essere reale poichè
mp+mπ>mn) in un protone e in un pione π –che,assorbendo un fotone, va a ricombinarsi nuovamente con p
e restituisce il neutrone n di partenza. L’nEDM è,
quindi, tanto più intenso tanto più la distanza d tra le
particelle virtuali p+ e π- è grande(nEDM=d*e con e
la carica del protone). ………………………………
nEDM è parametrizzato dalla seguente Lagrangiana efficace:
.
LnEDM= (1/2)dnnγ0iγ5σμνnFμν~d·E dove il tensore campo del fotone è Fμν=∂μAν-∂νAμ,
n è la funzione d’onda ψ per il neutrone, mentre σμν è il prodotto antisimmetrico delle
due matrici gamma di Dirac σμν=(1/2i) [γμ,γν]. In presenza del termine θ, nEDM può
essere trovato dal seguente elemento di matrici :
.
‹n(pf) γ(k)|eJμemAμi∫d4xLθ|n(pi)›=dnn(pf)γ0γ5σμνn(pi)kμεν(k)
dove Jμem è la corrente elettromagnetica dei quarks ψfγ0γμψf , εν(k) denota il
quadrivettore di polarizzazione del fotone,mentre il momento portato dal fotone,
kμ=(pf)μ-(pi)μ è uguale alla differenza tra i momenti dello stato finale e iniziale del
neutrone. Quello che si può immediatamente osservare è che al valore di dn
contribuisce Lθ e quindi il valore stesso di θ. Il calcolo dell’elemento di matrice alla
sinistra della precedente espressione è molto difficile in QCD, ma, nonostante ciò, nel
passato sono stati sviluppati diversi metodi di calcolo, di cui si presentano i risultati:
- il risultato del modello di calcolo bag fornisce un valore dn ~ θ ·2.7·10-16 e cm
- il metodo CL(logaritmo chirale): dn ~ θ·5.2·10-16 e cm
- il metodo ChPT(di perturbazione chirale): dn ~ θ·3.3·10-16 e cm
- il calcolo più recente deriva dal metodo SR(regola di somma): d n ~ θ·2.2·10-16
e cm.
8
Tutti i precedenti risultati hanno una considerevole incertezza, di almeno il 50%, che
riflette una varietà di incertezze inerenti ai calcoli non perturbativi in QCD. Benché i
risultati differiscono per fattori anche di numerose unità, si può comunque
dedurre,senza dubbio, che tutti concordano nell’ordine di grandezza, che dn|teorico~
θ·10-16 e cm. Questo numero deve essere confrontato con i più recenti risultati
sperimentali per l’nEDM: |dn|sperimentale<6.3·10-26 e cm da cui si può ricavare un
vincolo particolarmente restrittivo per il valore di θ: |θ|·10-16 <3.6·10-26→|θ|<10-9.
Concordiamo che se il valore di θ non è proprio nullo, deve essere innaturalmente
piccolo:non c’è ,però, nessuna ragione a priori per cui i due termini in θ̃, cioè θ e
arg(detM) debbano in qualche modo compensarsi e cancellarsi a vicenda con una tale
accuratezza,di almeno una parte su 10 9. E’ necessario,pertanto, un meccanismo
dinamico che spieghi il valore sperimentale di θ , forzandolo a rilassarsi a zero.
Prima di procedere ulteriormente,bisogna,però menzionare che ci sono altri effetti
che violano la simmetria CP che sono indotti dal θ termine, anche se ,nonostante ciò,
impongono limiti meno stringenti, per cui alla resa dei conti l’effetto dominante è il
problema dell’nEDM. Comunque, per esempio, un valore non nullo di θ dà origine ad
una ampiezza non nulla per il decadimento che viola CP η→π+π – calcolata
teoricamente come A~ θ²·1.8·10². Il limite sperimentale è < 1.5·10-3 che comporta
un vincolo
| θ|<3·10-3 , che è sicuramente molto più debole dell’altro.
3 PUO’ LA QCD RISOLVERE IL PROBLEMA CP STESSO ?
Ci chiediamo se un valore piccolo di θ può emergere in un modo credibile dalla teoria
di gauge o se può essere resa in un qualche modo nulla; si possono distinguere tre
possibilità:
1)se le interazioni che rompono P e T conducono ad una rinormalizzazione infinita di
θ, diremo che l’invarianza forte P e T è innaturale;
2)se l’interazione che rompe P e T conduce ad un valore di rinormalizzazione piccolo
di θ, diremo l’invarianza naturale. In questo caso, se un valore nudo θ=0 è imposto
per ragioni di simmetria, una teoria fisicamente accettabile può emergere senza
ulteriore aggiustamento.
3)in certe classi di teorie il parametro θ è fisicamente senza significato o determinato
dinamicamente. In questo caso, se l’interazione forte conserva P e T, diremo la
conservazione automatica.
Teorie di tipo 1) sono veramente prive di attrattiva perché fisicamente inaccettabili,
quelle di tipo 2) richiedono che sia P che T siano debolmente rotte, cioè che la rottura
avvenga attraverso un accoppiamento dimensionale nella Lagrangiana nuda, o
spontaneamente. Invece, una teoria di tipo 3) richiede che la massa di alcuni quarks
sia nulla o che un nuovo genere di particelle(che chiameremo Assioni) esista.
Così, se le nostre argomentazioni sono corrette, almeno una di queste quattro
condizioni deve verificarsi:
9
1)P è debolmente rotta-questa condizione conduce ad una maggiore conoscenza delle
proprietà del neutrino
2)T è debolmente rotta
3) la massa “nuda” di qualche quarks è zero: in questo caso ci sarebbe un interessante
parallelo tra il settore dei quarks e quello dei leptoni(quark senza massa e neutrino
senza massa)
4)un assione:questo è in qualche modo la possibilità più attraente e sicuramente più
eccitante.
Tra queste quattro alternative la conservazione P e T forte è naturale nelle prime due
e automatica nelle ultime due.
Prima di introdurre il campo dell’assione, cioè prima di invocare nuova fisica oltre la
QCD, un teorico può provare un punto di vista minimalista (che è quello che
comunemente viene adottato per fronteggiare ogni nuovo problema) per cui , senza
introdurre qualcos’altro di nuovo, si chiede se la QCD possa risolvere il problema CP
stesso, con i suoi strumenti,senza il bisogno di una nuova fisica.
Come già abbiamo anticipato, un’ ovvia soluzione di questo tipo, entro la QCD,
esiste: se ci fosse uno dei quarks senza massa, ad esempio mu=0, allora tutti gli effetti
di θ sarebbero nulli. In questo caso siamo nel limite chirale ,infatti, non essendoci il
termine di massa che rompe la simmetria, questo comporta l’esistenza di una
simmetria globale ma anomala UA(1) delle rotazioni chirali del campo del quark u:
uR→uRexp(iβ) e uL→uLexp(-iβ) che può ruotare via,cioè eliminare, il termine θ.
La relazione chiave qui è l’anomalia triangolare nella divergenza della corrente
assiale
∂μJμA=(g2n/(32π²))TrGμνG̃ μν + divergenza ”innocua”+0(quando m=0)
dove n è il numero di quarks bilineari nella
corrente assiale. L’anomalia deriva dal fatto
che la quadridivergenza totale nel processo,
A
noto come anomalia triangolare,è non nulla
il che comporta una violazione della legge di
J μA
continuità.
A
Anomalia
Se qualche quark ha massa nulla, allora,eseguendo
triangolare
l’opportuna rotazione chirale,secondo l’equazione
precedente,aggiungiamo o sottraiamo alla Lagrangiana una interazione della forma
TrGμνG̃ μν.
Infatti la trasformazione chirale che si opera è δChΓ(A)=αA(x)(g2n/(32π²))TrGμνG̃ μν ,
per cui l’azione diventa
S[A]=SYM+∫[(θ+αA(x))/(32π²)]GμνG̃̃ μνdx
dove SYM è l’azione di Yang-Mills che descrive il resto degli effetti della QCD non
violanti CP. E’ possibile scegliere, pertanto, il parametro di rotazione assiale αA(x)
tale che θefficace=θ+ αA(x)=0, eliminando, così, la presenza ingombrante di θ.
Comunque mu=0 non è sostenuto da basi fenomenologiche e pertanto questo scenario
dovrebbe essere scaricato al momento; il condizionale è d’obbligo poiché la massa
10
dei quarks misurata sperimentalmente è quella vestita di gluoni, mentre quella “nuda”
è estremamente leggera e ricavabile da valutazioni algebriche , le cui stime sono
ancora minate da troppe incertezze.
Una più intricata soluzione, entro la QCD, potrebbe esistere se lo stesso
confinamento forte fosse tale da garantire uno schermo per gli effetti del termine θ:
questa questione fu sollevata inizialmente da A. Polyakov poco dopo la scoperta del
problema CP. Le sue argomentazioni erano le seguenti: il termine θ compare nella
azione S come integrale su derivate totali, cioè una quadridivergenza, che può
operare,ossia dare contributo, soltanto se ci sono componenti non nulle a lungo
raggio dei campi di gauge. Come già si è detto, nell’approssimazione semiclassica,
tali componenti sono certamente presenti:è evidente dai calcoli degli istantoni.
Comunque si può sempre ribattere che tale approssimazione perde la più importante
caratteristica della QCD,cioè il confinamento di colore, che potrebbe eliminare tali
interazioni a lungo raggio(è il cosiddetto “schermo” di colore) e rendere pertanto
l’integrale nullo. Però tale argomento è stato studiato con una conclusione negativa,
in quanto ci sono ben due effetti in QCD che dipendono da tale schermo, non solo la
conservazione/violazione CP, ma anche la pesantezza della massa del mesone η’(il
problema UA(1) ).
Anche se non si conosce precisamente come funziona il meccanismo di
confinamento, sappiamo che η’ si separa dall’ottetto dei bosoni di Goldstone(sarebbe
più corretto parlare di pseudo-bosoni di Goldstone, poiché sono particelle i cui campi
definiscono le fluttuazione tra gli stati di vuoto,da cui la loro classificazione, ma
senza massa solamente nel limite chirale. L’ottetto è formato da :π 0,π+,π-,K0,K-,K+,K̃ 0
e η )[il simbolo ~ sopra K indica la sua antiparticella].
Il mesone singoletto di sapore, η’=(1/√3)(uγ0γ5u+dγ0γ5d+sγ0γ5s) è significativamente
più pesante dell’ ottetto di sapore di Goldstone, infatti m η’~958 MeV. Come venne
mostrato da Weinberg, se η’ fosse stato un bosone di Goldstone, la sua massa sarebbe
stata vincolata dal limite m η’≤ m π√3, in notevole contraddizione con i dati
sperimentali: questo suggerisce che η’ non è privo di massa nel limite chirale, al
contrario dei bosoni dell’ottetto.
La spiegazione del contributo extra alla massa di η’ deriva da effetti non perturbativi
dovuti all’anomalia assiale correlata proprio al termine θ: storicamente,infatti, il
problema UA(1) è stato un esempio, tipico nella fisica, in cui la soluzione di alcuni
problemi ne genera altri totalmente scorrelati e inaspettati(in questo caso il problema
CP).
Per quantificare l’effetto su basi teoriche, introduciamo il correlatore della densità di
carica topologica, definito in letteratura scientifica, semplicemente come la
suscettibilità topologica
χ=-i∫d4x‹0|TQ(x)Q(0)|0› dove Q=(1/(32π²))GaμνG̃ aμν
Si dimostra che nell’approssimazione dell’espansione 1/Nc dove Nc è il numero di
colori,la massa m η’ può essere definita come: m η’2=((6 χ)/(f²π))+o(mq)+o(1/ Nc²) con
fπ= costante di decadimento del pione. Quindi, affinché la massa di η’ sia non nulla
nel limite chirale, χ deve essere non nulla nella pura gluodinamica. Una gran quantità
11
di prove teoriche sono state accumulate negli ultimi 20 anni, che mostrano come χ
nella pura Yang-Mills non si azzera: gli studi con la regola di somma in QCD
conduce a χ≈(180 MeV)4≠0. Un valore diverso da zero della suscettibilità topologica
significa, per quanto detto, che c’è una richiesta del parametro θ in questa teoria.
Infatti χ non è niente altro che la derivata seconda dell’energia del vuoto rispetto a θ
preso a θ=0. Da questo si ricava che, in quanto QCD risolve il problema U(1), non
può risolvere da sola il problema CP forte senza un aiuto dall’esterno.
4 LA RICERCA DI SOLUZIONI OLTRE LA QCD: IL MECCANISMO DI
PECCEI-QUINN:
Il primo meccanismo dinamico che permette di risolvere il problema CP forte fu
proposto da Peccei e Quinn, i quali mostrarono che se il modello Standard ammette
una simmetria globale chirale U(1), nota in letteratura come simmetria U(1)PQ
(qL→qLexp(iα) e qR→qRexp(-iα)), allora la dinamica della teoria è tale che θ è
mandato a zero dinamicamente. Ovviamente, se LSM ha una addizionale simmetria
chirale che non è rotta,non c’è mai stato il problema CP poiché è analogo ad avere
quarks senza massa in cui la trasformazione chirale può ruotare via θ. Il caso fisico
interessante da considerare è,perciò, quello in cui LSM ha tale simmetria, ma questa
viene spontaneamente rotta, per cui deve esistere nella teoria un nuovo bosone di
Goldstone, una eccitazione di spin zero e con massa nulla. Questa eccitazione è il
nostro famoso assione, il cui campo sotto tale simmetria, essendo il campo di un
bosone di Goldstone,si trasla: a(x)→a(x)+δα·vPQ ,dove vPQ è un parametro di scala
associata con la rottura, mentre δα è il parametro infinitesimo della trasformazione.
Per una normale simmetria spontaneamente rotta, il fatto che i bosoni di Goldstone
traslino sotto la simmetria, implica che la Lagrangiana effettiva che governa la
dinamica di queste particelle può solo coinvolgere le derivate di questi campi ,in
quanto per a→a’=a+cost allora ∂μa→∂μa’=∂μ(a+cost)= ∂μa per cui L è lasciata
invariata. La simmetria U(1)PQ , comunque, poiché è chirale, soffre dell’anomalia di
Adler Bell Jackiw (l’anomalia triangolare):questo comportamento particolare della
Lagrangiana della teoria è riprodotto,semplicemente,dall’avere un termine lineare nel
campo dell’assione accoppiato all’anomalia,cioè a (g²/(32π²))TrGμνG̃ μν. Da qui, se il
modello Standard è caratterizzato da una rottura spontanea della simmetria U(1)PQ,
sarà allora descritto da una Lagrangiana efficace:
Leff=LSM+θ(g²/(32π²))GaμνG̃ aμν +a(ξ/vPQ)(g²/(32π²))GaμνG̃ aμν-½∂μa∂μa+L(∂μa,ψ)
dove ξ e L(∂μa,ψ) sono quantità dipendenti dal modello e da come vengono realizzate
le trasformazioni U(1)PQ per i fermioni nella teoria.
L’esistenza dell’interazione GG̃ che rompe U(1)PQ, dovuta all’anomalia chirale,
fornisce di fatto un potenziale per il campo assionico. Non è pertanto più vero che nel
vuoto tutti i valori di ‹a› sono permessi, infatti, includendo il contributo
dell’anomalia, uno trova che il valore di aspettazione del campo dell’assione nel
vuoto è fissato essere
‹θ|a|θ›=-θ vPQ /ξ (2)
12
Il campo fisico dell’assione è, naturalmente, l’eccitazione rispetto al valore di
aspettazione nel vuoto cioè afisico=a-‹θ|a|θ›=a+θ vPQ /ξ
Così, in termini di questo campo si ha che la Lagrangiana efficace si può riscrivere
come:
Leff=LSM+L(∂μafis,ψ) -½∂μafis∂μafis+ afis(ξ/vPQ)(g²/(32π²))GaμνG̃ aμν in cui
θ(g²/(32π²))GaμνG̃ aμν +a(ξ/vPQ)(g²/(32π²))GaμνG̃ aμν= (θ+ (aξ)/(vPQ))(g²/(32π²))GaμνG̃ aμν=
= afis(ξ/vPQ)(g²/(32π²))GaμνG̃ aμν
Pertanto, la presenza dell’ulteriore simmetria U(1)PQ ha condotto a zero θ, cioè ha
eliminato “dinamicamente” il parametro θ che viola CP, sostituendolo con
l’introduzione di un campo dinamico: l’assione.
Prima di proseguire, ci si può chiedere come si ricavi il risultato dell’equazione (2):
può essere mostrato esaminando le equazioni del moto del campo dell’assione.
Ritorniamo a Leff in cui compare ancora θ e in cui abbiamo a e non afisico; le
equazioni del moto saranno quelle che soddisfano le equazioni di Eulero-Lagrange in
forma quadrivettoriale:
∂μ∂L = ∂L
→ -∂μ∂μa+∂μ∂L(∂μa,ψ) = ξ g² GaμνG̃ aμν
∂∂μa ∂μa
∂∂μa
vPQ32π²
Se non ci fosse il termine di destra,cioè il termine di anomalia, è chiaro che qualsiasi
valore costante per il campo assionico nel vuoto sarebbe permesso; comunque,
l’equazione precedente ci informa che il campo dell’assione si fissa nel vuoto al
valore dove
‹ ∂Veff › =-ξg²
‹ GaμνG̃ aμν› =0
∂a
vPQ32π²
Il valore di aspettazione della densità che viola CP GG̃ è periodica nel rilevante
parametro θ della teoria: per esempio, in una approssimazione istantonica,‹ G aμνG̃ aμν›
è proporzionale a sen(θ+‹a›ξ/ vPQ ), perciò tale valore di aspettazione nel vuoto si
annulla precisamente quando l’equazione (2) è soddisfatta.
Benché l’introduzione della simmetria spontaneamente rotta U(1) PQ risolve il
problema forte CP, necessita la presenza di un nuovo campo dinamico nella teoria,
che si colloca al di là del modello Standard:l’assione.Questa eccitazione, che è senza
massa, perché è un bosone di Goldstone, acquista una massa come conseguenza della
anomalia chirale.
Infatti
ma²= ‹ ∂²Veff › = -ξg²
∂ ‹GG̃ ›
∂a²
vPQ32π² ∂a
‹a›=-(θ vPQ)/ξ
La massa dell’assione è proporzionale alla curvatura del potenziale effettivo indotto
dall’anomalia. Si può sottolineare che, puramente su basi dimensionali, la massa
dell’assione è dell’ordine ma²~Λ4QCD/ v2PQ dove Λ4QCD rappresenta la scala di
aspettazione di ‹GG̃ ›. Se vPQ >> ΛQCD si ottiene,come prezzo per risolvere il problema
CP dinamicamente, un bosone molto leggero.
13
5 GLI ASSIONI:
5.1 BREVE RASSEGNA SUI MODELLI ASSIONICI
ASSIONE DI WEINBERG-WILCZEK
Quando i campi di Higgs sviluppano i valori di aspettazione del vuoto, il gruppo di
simmetria elettrodebole è spontaneamente rotto e ciò dà massa ai bosoni vettori
intermedi W+, W- e Z. Simultaneamente, la simmetria globale U(1)PQ è
spontaneamente rotta: questo conduce all’emergere di un bosone di Goldstone senza
massa, l’assione in questo caso. Nel modello Standard con due doppietti di Higgs
l’assione è dato dalla seguente combinazione lineare
a≡(1/v)(vφImφ0-vχImχ0)
dove φ0 e χ0 denotano le componenti neutre dei doppietti di Higgs. Inoltre
v≡(vφ²+vχ²)½ ~250 GeV e vφ e vχ sono i valori di aspettazione del vuoto di φ e χ,
rispettivamente. In tutta questa approssimazione l’assione è ancora senza massa, ma,
come abbiamo già detto, effetti della QCD non perturbativi(come gli istantoni) danno
origine ad un potenziale per l’assione: da qui acquista una massa non nulla che può
essere stimata come ma ~(fπmπ)/v ~100KeV (3)
Inoltre, come appare da questo modello, la costante di decadimento dell’assione è
1/v, perciò sia la massa dell’assione che la costante di decadimento sono legati alla
scala v di rottura della simmetria elettrodebole. Questa si rivela essere una restrizione
troppo grande, perciò tale modello WW è escluso sulle basi degli esistenti dati
sperimentali.
ASSIONE KSVZ (KOTIKOV,SHIFMAN,VAINSHTEIN,ZAKHAROV):
Se la scala di rottura della simmetria è molto più grande di quella elettrodebole,
allora, secondo l’espressione (3) l’assione è molto più leggero e la sua costante di
decadimento è molto più piccola: tale assione “invisibile” non sarebbe in conflitto
con i dati sperimentali.
Per slegare l’assione dalla scala elettrodebole, bisogna disaccoppiare i corrispondenti
campi dai quarks noti e accoppiarli a ipotetici campi fermionici moto pesanti,
portanti colore. In maggior dettaglio, si introduce un campo scalare complesso Φ
accoppiato ad un ipotetico singoletto elettrodebole, cioè un campo di quark Q nella
fondamentale rappresentazione di colore: L= ΦQRγ0QL+Hermitiana coniugata
Il modulo di Φ è assunto sviluppare un grande valore di aspettazione del vuoto f/√2,
mentre il suo argomento diventa il campo a dell’assione:
a(x)=fα(x) α(x)≡ArgΦ(x) f>>Λ
Allora l’accoppiamento a bassa energia dell’assione al campo gluonico è
L=(a/(f32π²))GaμνG̃ aμν
così che la Lagrangiana QCD dipende dalla combinazione θ+α(x). In generale si
potrebbe introdurre più di un fondamentale campo Q, allora l’accoppiamento
14
assione-gluone acquista un multiplo intero
N e la Lagrangiana diventa
μν
L’=(Na/(f32π²))Ga G̃ aμν .
Questo fattore è qualche volta indicato come l’indice dell’assione ; il minimo assione
corrisponde a N=1. In generale LQCD dipende dalla combinazione θ+Nα(x) e, come
quanto detto precedentemente,gli effetti QCD non perturbativi generano un
potenziale per θ+Nα(x) che è minimizzato al valore θ+Nα(x)VUOTO=0 per cui il
problema CP forte è risolto automaticamente.
L’ASSIONE ZDFS (ZAKHAROV,DINE,FISCHLER,SUSSKIND):
Un modo alternativo per mantenere la simmetria PQ dei due doppietti del modello
Standard ma di separare le scale di rottura PQ e elettrodebole, si estende la
Lagrangiana SM tramite l’aggiunta di un singoletto di campo SM, Σ:
L=λuQLγ0ΦuR+λdQLγ0χ*dR+H.c.+V(Φ+Φ,χ+χ,(Φ+χ)(χ+Φ),Σ+Σ,(Φ+Σ)Σ²)
Questa è invariante sotto le seguenti trasformazioni assiali:
qL→qLeiα
qR→qRe-iα
Φ→Φe2iα
χ→χe-2iα
Σ→Σe2iα
Dalla rottura spontanea di questa simmetria emerge una particella di Goldstone, un
assione, come sovrapposizione a≡(1/V)(vΦImΦ0-vχImχ0+vΣImΣ)
Dove V=(vΦ²+vχ²+vΣ²)½ e vΦ,vχ e vΣ sono i valori di aspettazione del vuoto di Φ, χ e
Σ,rispettivamente. Il valore di aspettazione del vuoto di Σ non deve essere collegato
alla scala di rottura della simmetria elettrodebole, infatti può essere grande tanto
quanto la scala GUT: se è così l’assione è leggero e piccola è la sua costante di
decadimento.
5.2 RESTRIZIONI SULLA MASSA DELL’ASSIONE
Coma già spiegato, l’assione è uno pseudo-bosone di Goldstone che acquista massa:
i limiti fenomenologici su questa dovrebbero distinguere tra i casi KSVZ e ZDFS, in
quanto nei due scenari le costanti di accoppiamento alla materia dell’assione sono
diverse. Comunque, il presente scopo è quello di riassumere brevemente gli ordini di
grandezza di tali vincoli, da cui si può concludere che gli effetti che distinguono gli
assioni dei due modelli sono difficilmente osservabili.
Assioni leggeri possono essere prodotti dalle stelle nei seguenti possibili processi:
-processo Primakoff: γ↔a conversione che avviene nel campo elettromagnetico di
un nucleo
- fotoproduzione su un elettrone: γ +e-→e-+a
-bremsstrahlung nucleone-nucleone: N+N→N+N+a
o elettrone su un nucleo:e-+(A,Z) →e-+(A,Z)+a .
Con questi processi le stelle perdono energia, trasferita agli assioni prodotti. A meno
che 1/fa, che fissa la forza di accoppiamento con la materia del campo assionico, non
sia particolarmente piccola, la produzione eccessiva di assioni condurrebbe ad una
inaccettabile perdita di energia dalle stelle:questo comporta un limite inferiore nella
costante di decadimento dell’assione fa>109 GeV.
15
E’ notevole che la cosmologia fissi un limite superiore per f a, infatti se questo è
troppo grande, si ricava che 1/fa è troppo piccolo e come risultato, durante il corso
dell’evoluzione cosmologica dell’universo, gli assioni si sarebbero dovuti
disaccoppiare presto e avrebbero dovuto oscillare coerentemente. Ci sono due
meccanismi principali attraverso cui la densità di energia accumulata in queste
oscillazioni può essere dissipata:l’espansione di Hubble dell’universo e la produzione
di particelle per mezzo degli stessi assioni.
Comunque, se fa>1012GeV nessuno di questi meccanismi risulta efficace, poiché
l’accoppiamento assionico è poco intenso, e quindi, in qualche istante di evoluzione,
tale densità di energia avrebbe dovuto superare quella critica e avrebbe fatto
ricollassare l’universo, bloccandone l’espansione.
Riassumendo, si ottengono i seguenti ordini di grandezza su fa e, conseguentemente,
su ma:
109GeV<fa<1012GeV e 10-6 eV<ma<10-3 eV
6 ESPERIMENTO PVLAS(Polarizzazione del Vuoto con LASer):
6.1 MOTIVAZIONI:
Il vuoto quantistico può essere pensato come un mezzo simile ad un gas ordinario, la
cui struttura, comunque, è normalmente invisibile, paragonabile alla trasparenza
dell’acqua di uno stagno. Per “vedere” e analizzare la sua struttura, bisogna pertanto
perturbare il mezzo, così come nello stagno bisogna lanciarvi una pietra per studiare
il comportamento dell’acqua.
Quando si studia il vuoto quantistico l’idea è di porre come mezzo perturbante un
campo elettromagnetico esterno e usare come oggetto di investigazione per analizzare
i possibili cambi nella struttura indotti dal campo un oggetto che può interagire con
esso, cioè un raggio laser. Le proprietà del vuoto quantistico sono rilevate dal cambio
da esso indotto sullo stato di polarizzazione del raggio laser inizialmente polarizzato
linearmente: questo è alla base dell’esperimento PVLAS,misurante effetti di
birifrangenza e dicroismo.
Tratteremo la birifrangenza nella sessione successiva in modo più approfondito,
associandola direttamente al campo assionico, ma è utile per ora evidenziare
solamente gli aspetti qualitativi, per una comprensione più immediata. Lo scopo è
quello di inquadrarla ancora in un ambito classico per mostrarare maggiormente il
parallelo tra vuoto della QCD e i gas. Si definisce in Elettrodinamica classica per
mezzo birifrangente un mezzo che ha le proprietà di esibire un differente indice di
rifrazione per differenti direzioni del vettore di polarizzazione del raggio che lo
attraversa. Geniale è stato l’approccio di Fresnel nello studiare questi mezzi,
introducendo come utile strumento matematico l’astratto ellissoide degli indici i cui
semiassi hanno proprio il valore degli indici di rifrazione. Il caso più comune,
tralasciando quello banale della totale isotropia(la sfera, con un unico indice in tutte
le direzioni) è quello dei cristalli detti monoassici, cioè quelli definiti da un ellissoide
di rotazione in cui è possibile definire due indici di rifrazione, quello
straordinario,l’indice relativo all’asse ottico e quello ordinario relativo a qualsiasi
asse ortogonale a quello ottico. Da questo deriva la denominazione di mezzi
birifrangenti,in quanto, dato un raggio incidente, quello trasmesso si scinde in due
16
poiché risente dell’anisotropia del mezzo e del diverso comportamento indotto dai
due indici operanti in direzioni ortogonali tra loro. Il caso di nostro interesse è quello
di alcuni gas che in condizioni ordinarie, cioè non perturbati, si comportano
otticamente in modo isotropo, ma che eccitati da un campo elettrico o magnetico si
comportano come oggetti birifrangenti:tale fenomeno è noto come effetto CottonMouton per cui la differenza tra gli indici è Δn=nSTRAO-nORDIN=CλB² cioè è un effetto
quadratico nell’intensità del campo(C è una costante, mentre λ è la lunghezza d’onda
incidente). Utilizzando la Lagrangiana della QED si ottiene anche nel caso del vuoto,
introducendo un campo B esterno intenso, una espressione analoga: sembrerebbe
spiegato l’esperimento come puro effetto elettrodinamico, se non fosse che
l’ampiezza della birifrangenza, ma anche del dicroismo, è all’incirca 10 4 volte più
intensa di quella aspettata dalla sola QED. Questo è un’ indizio che manca qualcosa,
o meglio che la QED non spiega tutto ciò che si verifica nel processo.
Quanto al dicroismo, si intende con esso il comportamento di alcuni mezzi che
assorbono in proporzioni diverse l’onda ordinaria e quella straordinaria:
l’assorbimento dipende dall’angolo che la direzione di oscillazione del campo
elettrico forma con una particolare direzione tipica della sostanza. Dato un tipico
mezzo materiale di questa categoria, se le molecole che costituiscono la sostanza
sono allungate, avremo un grande assorbimento quando il campo elettrico E
dell’onda è parallelo all’asse della molecola e uno molto minore quando è
perpendicolare a esso. Una delle due onde viene progressivamente assorbita e diffusa
e, se lo spessore è sufficiente, scompare, mentre l’altra prosegue. Pertanto, se il
raggio incidente forma
un certo angolo rispetto a tale
direzione, le sue componenti finali, avendo sorti diverse,saranno tali che una rimane pressoché inalterata, mentre l’altra
fortemente ridotta, comportando
come risultato netto una apparente rotazione del vettore campo elettrico nella sua polarizzazione inizialmente lineare.
Ebbene, dall’esperimento PVLAS(INFN, Legnaro,Italia) sono emersi sperimentalmente tali processi indotti dal vuoto: come è possibile spiegarli? E’ possibile farlo
presupponendo che tale esperimento ha avuto la possibilità di produrre e rilevare nel
suo apparato assioni che hanno interagito con il raggio laser e con il campo esterno
inducendo tali processi, interpretabili alla luce dei calcoli della sessione 6.
Un fotone interagisce con un secondo
fotone virtuale(Bext) per produrre una
particella virtuale,l’assione. La particella
allora decade in un fotone reale e in uno
virtuale : il 2° processo è detto effetto
Primakoff, dal nome del fisico che per
17
primo lo ha discusso nei primi anni della fisica dei pioni(è un processo che riguarda
anche gli assioni che, in quanto pseudoscalari, hanno molte proprietà analoghe e
quindi partecipano a processi analoghi dei pioni neutri). Il primo processo è
chiamato, invece, conseguentemente, effetto Primakoff inverso; il processo totale è
chiamato effetto di RIGENERAZIONE DEL RAGGIO. Dal momento che l’assione
ha massa, si propagherà ad una velocità minore di quella della luce, cioè del raggio
incidente e pertanto il risultato netto sarà un ritardo del fotone reale in uscita. In
PVLAS questo processo apparirà come una ellitticità dovuta alla birifrangenza.
Un fotone interagisce con un secondo
fotone virtuale (Bext) per produrre in
questo caso una particella reale,
l’assione che a questo punto si propaga
indipendentemente. L’effetto netto è,
quindi, lungo la direzione in cui avviene
il processo, una perdita di fotoni del
raggio e pertanto della sua intensità: PVLAS registra in questo processo il dicroismo
indotto dal vuoto.
Avendo a questo punto un quadro introduttivo della situazione è necessario, per una
comprensione più approfondita, trattare il problema della birifrangenza evidenziando
matematicamente il collegamento con gli assioni.
6.2ACCOPPIAMENTO DEGLI ASSIONI CON IL CAMPO ELETTROMATICO E EFFETTI SU UN RAGGIO LASER:
Gli assioni sono particelle pseudoscalari come i pioni per cui è possibile ipotizzare un
analogo accoppiamento con un campo elettromagnetico esterno, descritto dalla
Lagrangiana efficace:
L=(a/4f)FμνF̃ μν=(-a/f)(E∙B) in cui Fμν indica il tensore elettromagnetico
(Per semplificarci le cose abbiamo rinormalizzato f per non portarci dietro 1/(8π²).
L’effetto dell’interazione di queste particelle con due fotoni può essere quello di
indurre piccoli cambi nello stato di polarizzazione di un raggio laser(primo fotone)
che si propaga in un campo magnetico(secondo fotone del processo). Possono essere
ricavate severe restrizioni sulla massa e sulla costante di accoppiamento dell’assione
attraverso l’osservazione di rotazioni del piano di polarizzazione e ellitticità del
raggio.
Con la tecnologia a disposizione e per piccoli valori della massa dell’assione ma<10-4
eV si può essere sensibili a valori di f alti fino a 1010 GeV, che si confrontano
favorevolmente con i limiti che si stabiliscono per f da considerazioni astrofisiche,
con tutti i vantaggi per una possibile verifica sperimentale in laboratorio.
Le equazioni del moto si ottengono tenendo conto delle azioni di Maxwell e di KleinGordon(descrive il moto dell’assione libero), per il campo elettromagnetico e per
quello pseudoscalare rispettivamente a cui si aggiunge l’interazione definita
dall’espressione precedente. La Lagrangiana totale si compone,quindi, di:
18
L=LKG+LEM+LINT=(1/2)∂μa∂μa-a(m²/2)-(1/4)FμνF̃ μν +(1/(4f))aFμνF̃ μν dove m è il
termine di massa della particella pseudoscalare e
Fμν= Fμνext+ Fμνraggio=(∂μAνext-∂νAμext)+(∂μAνraggio-∂νAμraggio)=∂μAν-∂νAμ dove
Aμ = Aμext+ Aμraggio è il quadripotenziale totale. Fμνext rappresenta il tensore campo
esterno, che ha come componenti solo il campo magnetico costante, mentre Aμraggio è
il quadripotenziale associato all’onda luminosa, cioè al raggio laser.
Per semplicità poniamo la condizione di gauge
∙ A=0 e l’ulteriore condizione
A0=0 in quanto la propagazione è ortogonale a B. Tenendo soltanto i termini lineari
in A e a, si ottiene il sistema di equazioni accoppiate:
1) ∂μ ∂L
∂∂μa
= ∂L → □a=-m²a+(1/(4f))aFμνF̃ μν ma siccome (1/4) FμνF̃ μν =-B∙E=∂A∙B
∂a
∂t
valendo l’equazione E=- ∂A/∂t si ottiene la prima equazione del sistema :
(-1/f)B∙(∂A/∂t)+ (□+m²)a=0
2) ∂μ ∂L = ∂L con ∂L =0
∂∂μAν
∂Aν
∂Aν
→-(1/f)∂βaεβαλμ ∂λAμ =-(1/f)(∂a/∂t)
Quindi il sistema da risolvere è:
×A=-(1/f)B(∂a/∂t) →-□A-(1/f)B(∂a/∂t)=0
1)
2)
□A +(1/f)B(∂a/∂t)=0
-(1/f)B·(∂A/∂t) +(□+m²)a=0
(5)
Siccome compare la relazione B·(∂A/∂t), questo comporta che solo la componente di
A parallela a B è di interesse fisico, mentre nel caso in cui il raggio sia polarizzato
linearmente ortogonalmente a B l’effetto è nullo. I fotoni paralleli a B si mescolano al
campo assionico a; ricerchiamo delle soluzioni lineari, cioè
A\\=Ae -i(ω’t-k·x)
e
a=a0e -i(ω’t-k·x)
Queste soluzioni esistono se ω’ è scelto in modo da risolvere il sistema (5):
1)(k²-ω’²) A\\+(1/f)Ba(-iω’)=0
2)( k²-ω’²+m²)a-(1/f)B A\\(-iω’)=0 → (1/f)(-iω’)B A\\=( k²-ω’²+m²)a
→ A\\=(f/(-iω’B))( k²-ω’²+m²)a che sostituito in 1) mi restituisce
ω’4+ ω’²(-2k²-(B²/f²)- m²)+ k4 + m²k² =0
19
→ ω’²= ω±² =k²+(1/2)[m²+(B²/f²)±√ (m²+(B²/f²))²+(4B²f²) /f²] =k²+δ±
Una soluzione unica si ottiene imponendo le condizioni fisiche iniziali:
A\\(t=0,x=0)=1 e
a(t=0,x=0)=0
Infatti da A\\(x,t)=(A\\+exp(-iω+t)+A\\-exp(-iω-t))e-ik·x e
a\\(x,t)=(a+exp(-iω+t)+a-exp(-iω-t)) e-ik·x
sostituendo si ha che (-ω±²+k²)A\\± +(1/f)(-iω±)a±B=0 → a±=[( k²-ω±²)f A\\±]/(i ω±B)
con t=0 a++a-=0 →[( k²-ω+²)/(iωB)]fA++ [(k²-ω-²)/(iω-B)]fA- =0
Scegliendo
A±=(Aω±)/(k²-ω±²) → A\\=Ae-ik·x[(ω+/( k²-ω+²))exp(-iω+t)-(ω-/( k²-ω-²)) exp(-iω-t)]
A questo punto si sfrutta la 2° condizione A\\(0)=1=A[(ω+/( k²-ω+²))-(ω-/( k²-ω-²))].
La soluzione finale è A\\(x,t)= e-ik·x[( k²-ω-²)ω+exp(-iω+t)-(k²-ω+²)ω-exp(-iω-t)]/D(k)
Con D(k)= (k²-ω-²)ω+-(k²-ω+²)ω(6)
Siamo, quindi, finalmente pronti a trattare il caso più generale, quello in cui l’onda è
polarizzata linearmente ad un angolo α rispetto a B all’ingresso nella regione dove
c’è il campo, che poniamo a t=0; basta,infatti, scomporre il potenziale vettore che la
descrive nelle due sue componenti,parallela e perpendicolare a B:
A(0)=(cosαi+senαj) e-ik·x dove i e j sono i versori della direzione di B e a questa
ortogonale. Dopo un tempo t=L(L è la distanza percorsa in un tempo t, infatti
dobbiamo ricordare che stiamo operando in unità naturali per cui c=1)
A(L)=(cosαA\\(L)i+senαe-iωLj)e-ik·x (7)
cioè l’effetto si presenta solo sulla componente parallela a B con A\\(L) della forma
precedentemente calcolata.
Siccome la correzione su A\\ è piccola, è possibile approssimarla con l’utile
espressione:
A\\(L)=[1+ε(L)+iφ(L)] e-ik·x
con ε e φ quantità molto piccole. All’ordine più basso in ε e φ l’equazione (7)
rappresenta una onda che è polarizzata ellitticamente. Infatti data
A=cosα (1+ε(L)+iφ(L))i+senαj =Axi+Ayj
20
in coordinate cartesiane, è utile riscriverla scomponendola in onde sferiche
A=A+ε++A-ε- con
ε±=(i+ij)/√2 poiché si dimostra in elettrodinamica che se il rapporto A -/A+ è un
numero complesso, reiθ, allora l’onda è polarizzata ellitticamente con semiasse
maggiore ruotato rispetto l’asse x(la nostra direzione di B) di un angolo α=θ/2. Il
nostro scopo è, quindi, trovare questo angolo α.
In coordinate sferiche
A=(ε+/√2)[cosα(1+ε)+i(φ-senα)]+(ε-/√2)[cosα(1+ε)+i(φ+senα)]
C=E-/E+=[cosα(1+ε)+i(φ+senα)] [cosα(1+ε)-i(φ-senα)]/[ cos²α(1+ε)²+(φ-senα)²]
→ α’=α(L)~α- (ε(L)sen2α)/2
Il vettore potenziale descrive un’ellisse con asse maggiore ad angolo α(L) rispetto
alla direzione di B con una variazione rispetto all’inclinazione iniziale α di
polarizzazione lineare.
La figura è direttamente
riferita non al potenziale
vettore A ma al campo
elettrico del raggio (discorso analogo si estende per quello magnetico).
Sempre prendendo spunto dal caso elettrodinamico in cui l’ellitticità e, cioè il
rapporto tra il semiasse minore e quello maggiore, è (1-r)/(1+r), determiniamo prima
r, cioè il modulo del numero complesso E-/E+, sempre al 1° ordine in ε e φ:
r= cos2α+2εcos²α+isen2α(1+ε)
cos²α(1+ε)²+(φ-senα)²
→ l’eccentricità della polarizzazione ellittica sarà e~(1/2)|φ(L)|.
Siccome la rotazione netta α(L)-α dipende dal segno di α che cambia se, fissato B, si
cambia la direzione del raggio, cioè K (questo viene fatto per ottimizzare il percorso
totale dato lo spazio a disposizione, tramite riflessioni multiple), allora non è
possibile sperimentalmente accumulare l’effetto di rotazione se si fa viaggiare il
raggio laser avanti e indietro nel magnete, mentre è possibile farlo per l’effetto di
ellitticità. Quindi, anche se gli effetti sono molto piccoli, se la distanza totale da
percorrere è grande, l’ellitticità è più facilmente rilevabile.
21
Per trovare ora ε e φ nel nostro caso, bisogna fare una distinzione tra diverse
situazioni realizzabili sperimentalmente(e non), caratterizzate da variazioni lente o
rapide dei fattori di fase che compaiono nell’espressione di A\\(t,x) rispetto al fattore
di fase e -iωt della componente ortogonale non modificata.
1° caso: |ω±-ω|L<<2π le ω± sono estremamente vicine a ω, cioè l’effetto
dell’interazione del campo assionico è minimo e conseguentemente sia A\\ che φ si
propagano coerentemente a A┴ per tutto il processo. Possiamo, quindi, espandere ω±
intorno a ω: ω±² =ω²+δ± → ω± =ω√1+(δ± /ω²) ~ ω+(δ± /(2ω))
→ exp(-i ω±t)~e-iωtexp(-iδ±t/(2ω))~ e-iωt[1-(iδ±t/(2ω))-(δ±²t²/(8ω²))+(iδ±³t³/(48ω³))]
Per cui nell’espressione (6) D(k)~-δ-(ω+δ+/(2ω))+ δ+(ω+ δ-/(2ω))=ω(δ+-δ-)
Invece per il numeratore dell’espressione di A\\ data sempre da (6):
N~ [ ω+ δ+ (- δ-) 1- iδ+t - δ+²t² + iδ+³t³ +δ+ ω+ δ- 1- iδ-t – δ-²t² + i δ-³t³ ]eik·x-iωt
2ω
2ω 8ω² 48ω³
2ω
2ω 8ω² 48ω³
Tralasciando al momento la parte esponenziale, si ha quindi che, eseguendo tutti i
prodotti utili:
N~ω(δ+- δ-) + [(δ+ δ-t²(δ+- δ-))/(8ω)]-[(i δ+δ-t³(δ-²-δ+²))/(48ω³)]
Dato che A\\=N/D(k) allora A\\ ~ eik·x-iωt [1+ (δ+δ-t²/(8ω²)) –[(iδ+ δ-(δ++δ-)t³)/(48ω4)]
Confrontandola con l’espressione A\\~[1+ε(L)+iφ(L)] e-ik·x-iωt, utile per raccordare il
discorso a quello dell’ellitticità e dell’angolo α(L) si trova, tenendo conto le relazioni
δ+δ-=-k²B²/f² δ++δ-~m² t=L e k=ω (operiamo in unità naturali)
che:
ε(L)~(δ+δ-t²)/(8ω²)=-(B²L²)/(8f²) e φ(L)~-[(δ+δ-(δ++δ-)t³)/(48ω4)]=(m²B²L³)/(48f²k²)
La condizione al bordo di questa regione può essere posta arbitrariamente come:
|ω+ - ω-|L=2π dove la ω+ cessa di propagarsi coerentemente. Riferita ai parametri
fisici, tenendo conto sempre dell’espansione di ω+ rispetto a ω:
(|δ+|L)/(2ω)=2π →
| δ+|=(4πω)/L ma δ+~m²+B²/f²
per cui
m²~((4πω)/L)- B²/f²= ((4πω)/L)[1-(B²/f²)(L/(4πω))]
Siccome ω=(2π)/T e approssimativamente T=t/2 dove t è il tempo di andata e ritorno
del raggio e T=L allora m²~((4πk)/L)[1- ((B²L²)/(4²π²f²))] che riscrivo come
m²=m0²[1-(f0/f)²] definendo come parametri di riferimento m0²=(4πk)/L e f0=BL/(4π).
22
2° caso: |ω+-ω|L>>2π>>|ω--ω|L cioè continua a propagarsi coerentemente solo l’onda
con frequenza ω- .Espandendo, quindi, soltanto ω- intorno a ω nell’unico termine
coerente in questo caso nell’espressione (6), cioè quello in exp(-iω-t) si ottiene:
il termine da trattare è A= (ω+²-k²)ω- exp(-iω-t) = exp(-iω-t)
= exp(-iω-t)
(k²-ω-²)ω+-(k²-ω+²) ω1- (k²-ω-²)ω+
1 – δ-ω+
(k²- ω+²) ωδ+ωIl termine esponenziale lo tratto come exp(-iω-t)~(1-(iδ-t/(2ω))exp(-iωt)
Invece 1/[1-(δ-ω+/ δ+ω-)]~1+(δ-ω+/ δ+ω-)
Pertanto A ~[1+(δ-ω+/ δ+ω-)][1-(iδ-t)/(2ω)]e-iωt ma 1/ω-~[1- δ-/(2ω²)](1/ω)
Ne consegue che A~ e-iωt 1- iδ-t 1+ ω+ 1 - δ- δ- ~ e-iωt 1- iδ-t + ω+δ- =
2ω
ω
2ω² δ+
2ω ωδ+
-iωt
= e (1+ε(L)+iφ(L))
Si ricava, quindi, in questa regione le relazioni utili:
ε(L)~ (ω+ δ-)/(kδ+)
e
φ(L)~- (δ-t)/(2ω)=-(δ-L)/(2ω)
3° caso: |ω±-ω|L>>2π In questa regione c’è una completa incoerenza di A\\ che è
trasformato in una miscela di fotoni e particelle pseudoscalari:l’effetto di
accoppiamento del campo assionico è prevalente;situazione alquanto irrealistica.
Infatti si può notare che ,siccome sono invertite le condizioni rispetto al caso 1, la
condizione al bordo di questa regione sarà data dalla relazione inversa:
m²=m0²[(f0/f)²-1]>0
Questa regione corrisponde a valori completamente irrealistici di f, cioè f< f0 che
dipende dall’interazione con B(ricordarsi che la forza di accoppiamento del campo
assionico a quello elettromagnetico è data da 1/f e pertanto più f è piccolo più questa
è intensa, ma in questo caso la sua intensità è superiore di molto a quella riscontrata
sperimentalmente). Pertanto questo 3° caso definisce una condizione puramente
matematica ma non riscontrabile in nessun caso in laboratorio.
Consideriamo ora le condizioni sperimentali dei primi due casi che sono
realisticamente possibili: m0 stabilisce il range di massa m della particella interagente
con il campo a cui è sensibile l’esperimento di birifrangenza; dalle formule
precedenti si ricava che tutti gli effetti si annullano per m >> m0 per cui il contributo
di mesoni pseudoscalari che hanno accoppiamento simile, come π0 e η0 è non
misurabile. Analogamente f0 stabilisce il limite della scala per f anche se, data la
maggiore sensibilità nella sua misura e poiché gli effetti decrescono più lentamente
rispetto a quelli di m per f >> f0, è possibile analizzare anche grandi valori di f (cioè
particelle con scarsa forza di accoppiamento).
Abbiamo ora il pieno e completo apparato matematico per poter comprendere
l’apparato e i risultati ottenuti dall’esperimento PVLAS.
23
6.3 APPARATO E RISULTATI:
Prima di riportare i risultati dell’esperimento e commentarli è importante e
chiarificante,oltre che istruttivo, dare una descrizione dell’apparato.
L’esperimento opera con un
ellissometro che è capace di
misurare, con una sensibilità di 10-7 rad Hz-½, ampiezza e fase sia dell’ellitticità
che del dicroismo: si è
cominciato nel 2001 e già da
alcuni anni si sono osservati
chiari picchi dello spettro di
Fourier del rilevatore dove
segnali di autentico dicroismo e ellitticità dovrebbero
apparire. L’ampiezza di questi picchi (misurati con una pressione residua minore di
10-7 mbar e con un raggio laser di lunghezza d’onda λ=1064 nm(vicino infrarosso)
fino al 2004) è al livello di 10-7 rad ed è ben al di sopra del rumore della frequenza
dello spettro(il rapporto del segnale sul background magnetico è di solito migliore di
8 per giro, durevole più di 600 sec).
Il raggio laser polarizzato si propaga nel vuoto in un campo magnetico in una regione
di lunghezza L=1 m, generato da un dipolo magnetico superconduttore che opera ad
intensità superiori a 5.5 T; le linee di campo sono orizzontali e,anche se per
semplicità nella trattazione della sessione 6 avevamo posto B costante, in realtà
sperimentalmente il magnete può ruotare debolmente intorno ad un asse verticale che
coincide con la direzione di propagazione del raggio, al fine di ottenere effetti di
ellitticità e dicroismo modulati dalla frequenza di rotazione del sistema e pertanto
nettamente distinguibili dal rumore insito nella strumentazione elettronica adottata.
Per incrementare il cammino ottico attraverso il magnete(ricordiamo che l’angolo
α(L) non si accumula con il percorso ma l’ellitticità si), la luce viene riflessa tra due
specchi M1 e M2 installati rispettivamente sotto e sopra il magnete; la loro distanza è
d=6.4 m.
I due specchi formano la
cavità ottica detta di
FABRY-PEROT:la luce in
media è soggetta
a N
riflessioni e N è dell’ordine
di 105.
Luce polarizzata linearmente è immessa dentro la
24
cavità FP attraverso un polarizzatore, collocato dietro il magnete, P1, la cui
orientazione è mantenuta fissa per tutte le misure. Un polarizzatore P2 identico a P1 è
montato davanti al magnete,dietro M2 e è orientato ortogonalmente a P1 con un
ottimo aggiustamento in modo da minimizzare la trasmissione con il magnete della
luce proveniente dalla cavità(massima estinzione); infine un fotodiodo D analizza la
luce emergente da P2. Al fine di aumentare il segnale sul background è usata una
tecnica Heterodyne: per questo scopo una piccola elliticità di ampiezza circa 10 -3 rad
è data al raggio che emerge da M2,tramite un modulatore elettro-ottico che è guidato
da un preciso generatore a pulsazioni sinusoidali alla frequenza ω s=506 Hz. Inoltre,
come già è precedentemente emerso, il magnete è posto in rotazione ad una frequenza
fissa ωm e pertanto gli effetti di ellitticità e dicroismo sono modulati a 2 ωm ; la
posizione angolare del magnete è misurata da un set di 32 tracciatori sul perimetro
della piattaforma rotante di supporto: l’identificatore di ogni tracciatore e il suo
tempo di passaggio attraverso una stazione di misura sono continuamente registrati,
così da poter correggere accuratamente nell’analisi dei dati di Fourier la non
uniformità della velocità di rotazione del magnete(che altrimenti altererebbe i
risultati).
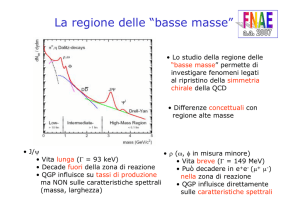
LA MISURA MOSTRA DATI
OTTENUTI NELL’OTTOBRE
2004 NEL VUOTO(<10-7mbar)
E A VARIE PRESSIONI DI Ne
CRESCENTI DA 1 A 21 mbar.
I puntini circolari danno i valori
di ellitticità, mentre i triangolini
rossi indicano il dicroismo.
Le ordinate danno l’effetto del
transito del raggio attraverso 1m
di una regione a B trasverso di
1T.
(I termini all’estrema sinistra,
ottenuti a vuoto spinto, non sono
dei veri e propri segnali poiché si discostano dagli altri).
Sono state eseguite diverse misure sotto diverse condizioni sperimentali, al fine di
comprendere le fonti del segnale dei picchi nello spettro di Fourier modulato 2ω m e
sono pertanto emersi i seguenti fatti:
-il picco dell’ampiezza è indipendente dalla frequenza della rotazione del magnete
nella misure di ellitticità;
25
-con il magnete non alla massima potenza, cioè con campo B non particolarmente
intenso, il segnale non è più presente(sintomo che è la grande intensità alla base del
processo);
- con gli specchi M1 e M2 della cavità FP rimossi, tali da ridurre il percorso da NL(N
è il numero di riflessioni e L la lunghezza della cavità) a semplicemente L, il segnale
scompare;
-con lo specchio M1 messo in avanti vicino a M2 in modo da rendere più piccolo il
percorso nella cavità, ma mantenendo uguale il numero N, il segnale non è stato
rilevato con la sensibilità disponibile delle apparecchiature;
- l’ampiezza 2 ωm del segnale di ellitticità generato dall’effetto Cotton-Mouton per
l’introduzione del gas nel percorso ottico è proporzionale alla pressione del gas.
Il gas è introdotto per un semplice motivo: la sua introduzione, oltre a generare
l’effetto CM classico che si addiziona a quello quantistico del vuoto, aumenta l’indice
di rifrazione del mezzo in cui la luce si propaga da 1 a n e pertanto rallenta il raggio,
mentre non ha effetto sulla propagazione di particelle ultraleggere che hanno
accoppiamento alla materia quasi nullo, in questo caso gli assioni(diminuirà pertanto
la discordanza tra le loro velocità e conseguentemente l’ellitticità osservata).
Però l’effetto della dipendenza dell’indice di rifrazione n dalla pressione è analogo, o
meglio è equivalente, al cambio, dipendente dalla pressione, della massa m dei bosoni
pseudoscalari:cambiando la pressione P, perciò, ci si sta muovendo lungo una curva
di diffrazione nel piano (ma,fa). Se il livello del rumore è abbastanza alto, con
l’aumento della pressione ci si aspetta di osservare una decrescita del segnale di
dicroismo fino a zero seguito da un comportamento oscillante: questo è in verità
visibile. A pressione zero il segnale di dicroismo del vuoto è massimo (è l’effetto
limpido del vuoto, svincolato da tutti gli effetti devianti indotti dalla materia), ma non
può essere osservato direttamente a causa dei limiti sperimentali del massimo vuoto
spinto raggiungibile e perché per piccoli valori di P i risultati non sono
particolarmente attendibili poiché si aggiungono all’effetto totale quelli del
background dell’apparato. Quello che si è fatto è stato, quindi, eseguire misure a P
decrescente ed estrapolare, perciò un best fit dei risultati finali sperimentali.
Se effettivamente l’origine microscopica dell’ellitticità e del dicroismo è dovuta
all’esistenza di assioni o comunque in generale a un qualche bosone leggero che si
accoppia a due fotoni con fa la costante di decadimento e ma la massa, allora
l’intersezione nel piano (ma,fa) delle due bande di curve di equiellitticità e di
equidicroismo identificano una regione relativamente piccola nel piano intorno a
ma = 10-3eV ( 1.0·10-3eV<ma<1.5·10-3eV) e fa=106GeV cioè g=1/fa~(1.7-5.0) 10-6
GeV-1(avendo osservato una rotazione della polarizzazione del raggio laser Δθ ~10 -12
rad).
Risultati notevoli, se non fosse che questa “oasi” è profondamente all’interno della
regione di esclusione del plot mappato da ricerche sugli assioni in altri campi(ad
esempio rispetto ai limiti astrofisici si rileva una forza di accoppiamento 6 ordini di
grandezza più intensa, 10-6GeV-1 contro i 10-12GeV-1)
26
7 COMMENTO DEI RISULTATI DA PVLAS E CONCLUSIONI:
Chiaramente, uno pseudoscalare con le proprietà precedentemente definite è
difficilmente compatibile con un assione genuino della QCD nei due modelli validi
precedentemente definiti, ma non solo. Tale particella dovrebbe avere proprietà
veramente peculiari per eludere le restrizioni rigide date su g dalle considerazioni di
perdita di energia stellare e dalla sua non osservazione in elioscopio al CERN tramite
l’Axion Solar Telescope(“Solar(CAST)”).
Figura:
grafico ma (massa
assione) vs g(costante di accoppiamento fotone-assio
ne) per attuali e futuri esperimenti.
Quelli che adottano il
laser hanno come
scopo la produzione e rilevazione di
assioni in laboratorio,esperimenti sulla materia oscura galattica impiegano cavità a microonde per
evidenziare gli assioni, sotto l’assunzione che questi siano costituenti essenziali del
nostro alone galattico; infine gli esperimenti solari ricercano assioni generati dal Sole.
In ogni caso un decisivo e indipendente test sperimentale del risultato di PVLAS è
richiesto urgentemente: una possibilità è offerta dalle collisioni ad alta energia di e +eal KEK dove si potrebbero ricercare eventi di singolo fotone più energia traversa
persa nello stato finale.
Le possibilità migliori e più tempestive, comunque, sono quelle offerte da
esperimenti di rigenerazione di fotoni che attraversano un assorbitore, sia basati su
laser ottici ordinari sia su raggi X da laser da elettroni liberi(FEL) al DESY e allo
SLAC. Infatti, come si può vedere dalla figura precedente, la regione dello spazio dei
parametri esplorata da PVLAS potrebbe essere verificata se si allestisse un
esperimento di rigenerazione di fotoni, sfruttando il già operante FEL al TESLA di
DESY che dispone di due dipoli magnetici superconduttori del tipo usato al collider
HERA di protoni-elettroni sempre al DESY. La radiazione usata, con una potenza
media <P>=20-40 W e ω=10-200 eV permetterebbe una determinazione precisa di m
e quindi una eventuale verifica ai risultati di PVLAS.
27
Conferme sperimentali dell’esperimento PVLAS, pertanto, ancora si attendono e
dall’esito ci si muoverà di conseguenza: se c’è una conferma e questa è dovuta ad una
nuova particella che interagisce con i fotoni sarà necessario un modello che spieghi
perché i limiti astrofisici finora trovati non siano validi e da quale nuovo meccanismo
vengano violati.
Dai lavori più recenti di PVLAS sembra, però, che emergano al contrario di quanto si
era prospettato all’inizio, dei risultati che smentiscono i precedenti che potrebbero
essere dovuti ad errori sistematici. L’obiettivo principale è quindi ancora quello di
valutare l’autenticità delle misure (confrontandole con nuove) e poi trovare una
spiegazione che sicuramente è più articolata di quella qui proposta: potrebbe essere
collegata o allo scambio di specie diverse di bosoni, a processi a più fotoni o a diversi
U(1) che si “mescolano” con quello elettromagnetico (fattore comune è comunque la
sovrapposizione di più processi).
28
8 BIBLIOGRAFIA:
-“Elettrodinamica classica” di John David Jackson
-“Advanced quantum mechanics” di J.J. Sakurai
-“Lezioni di meccanica quantistica relativistica” di A.Bottino e C.Giunti
-“Introduzione alla teoria dei campi” di Marcello Ciafaloni
-“Nuclear and particle Physics” di Burcham e Jobes
Articoli:
-“Axion interpretation of the PVLAS data?” di Andreas Ringwald
-“Axions, their relatives and prospects for the future” di Joerg Jaeckel
-“Axions-Motivation,limits and searches” di G.G.Raffelt
-“Problem of strong P and T invariance in the presence of instantons” di F.Wilczek
-“The strong CP problem” di R.D.Peccei
[n] The Strong Cp Problem.
R.D. Peccei (DESY) . DESY-88-109, Aug 1988. 49pp.
To appear in review volume: CP Violation, edited by C. Jarlskog.
Published in Adv.Ser.Direct.High Energy Phys.3:503-551,1989
-“QCD vacuum and axions: what’s happening?” di Gregory Gabadadze e M.Shifman
-“Effects of nearly massless, spin zero particles on light propagation in a magnetic
field” di Maiani, Petronzio e Zavattini
-“QCD axion and quintessential axion” di Jihn E.Kim
-Sito Internet:www.TS.INFN.IT/attivita/PHYSiCS/experiments/PVLAS/
29
30