Problema 1
PROBLEMA 1
x2
xn
Sia f la funzione definita da f ( x) 1 x ... e x
2!
n!
dove n è un intero positivo e x ∈ R
xn
1. Si verifichi che la derivata di f (x) è: f '( x) e x n
n!
2. Si dica se la funzione f ammette massimi e minimi (assoluti e relativi) e si provi che, quando n è
dispari, f (x) ≤ 1 per ogni x reale.
3. Si studi la funzione g ottenuta da f quando n = 2 e se ne disegni il grafico.
4. Si calcoli
2
0
g ( x)dx e se ne dia l’interpretazione geometrica.
Soluzione.
x2
xn
f ( x) 1 x ... e x
2!
n!
x x2
x n1 x
x2
xn x
f '( x) 1 ...
e
1
x
...
e
(n 1)!
2!
n!
1 2!
a)
xn x
e
n!
xn x
b) f '( x)
e 0
(n)!
Per n pari ho l’esponenziale sempre positiva e quindi
f '( x)
x n 0 da cui x n 0 mai verifica perchè
sempre positiva. e nulla per x=0 quindi ho un flesso a tang. orizzontale.
n dispari f '( x)
xn x
e 0
(n)!
xn 0
xn 0
x0
ho un massimo per x=0
02
0n 0
Dato che per n dispari ho un massimo per x=0 f (0) 1 0 ... e 1 e quindi
2!
n!
Il valore massimo è 1 da cui . f ( x) 1
x2 x
3) f ( x) 1 x e
2
C.E. ;
x2
x2
f ( x) 1 x e x 0 1 x 0 dato che l’esponenziale è sempre positiva
2
2
1
E dato che 1 4 1 0 anche l’espressione di 2 grado è sempre positiva e mai nulla.
2
Quindi f ( x) 0 sempre
f (0) 1 da cui passa per A(0,1)
x2 1
x2 x
lim 1 x e lim x 0 A.O y=0
x
x 2e
2
x2 x
f '( x) e per x=0 Flesso a tangente orizzontale in A
2
2 x x x 2 x e x 2
e e
x 2x 0
2
2
2
Flesso in A e in B(2,5e2 )
f '( x)
2
x2 x
x2 x
x
x
1
x
e
dx
e
xe
e dx
0
0
2
2
2
Dato che
xe
x
dx xde x ( x(e x ) e x dx) x(e x ) e x e
x2 x
x2 x
x2 x
x2 x
x2 x
x
x
e
dx
de
(
(
e
)
xe
dx
)
(
e
)
xe
dx
(e ) x(e x ) e x
2
2
2
2
2
Ho che
2
2
2
x2 x
x2 x
x
x 2
x x
1
x
e
dx
(
e
)
2
x
(
e
)
3
e
|
e
2 x 3 |0
0
0
2
2
2
2
2
2
2
2
x x
x x
x
x 2
x x
0 1 x 2 e dx 2 (e ) 2 x(e ) 3e |0 e 2 2 x 3 |0
2
x2 x
e2
2
1
x
e
dx
e
9
3
3
2,17
0
2
9
Che rappresenta l’area compresa tra le rette x=0 , x=2 (flessi) , y=0 e f(x)
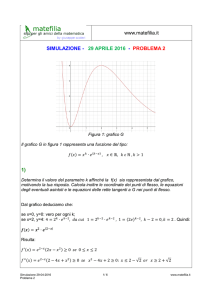
Problema 2
f ( x) x3 kx
f ( x) x( x 2 k )
f '( x) 3x 2 k
f ''( x) 6 x 2
Per k 0
sempre crescente (non presenta massimi e minimi)
con flesso in 0 a tangente obliqua.
Per k 0
sempre crescente (non presenta massimi e minimi)
con flesso in 0 a tangente orizzontale
Per k 0 presenta un massimo per x
k
k
e un min per x
3
3
con flesso in 0 a tangente obliqua
2) g ( x) x3 y 1 x
Mettendo a sistema ho che x 3 1 x da cui x3 x 1 0
Considerata la funzione
f ( x) x3 x 1 nell’intervallo 0,1 ho che f (0) 1 f (1) 1
Per il teorema degli zeri ho almeno una soluzione .
Dato che f '( x) 3x3 1 è sempre positiva ho una sola soluzione.
f ( x0 )
f ( xn 1 )
Per il metodo delle tangenti. x0 x1 x0
…. xn xn 1
f '( xn 1 )
f '( x0 )
x
0,5
0,714286
0,68318
0,682328
0,682328
f(x)
-0,375
0,078717
0,002043
1,49E-06
1,41E-12
f'(x)
1,750001
2,530613
2,400205
2,396717
2,396715
3) g ( x) x3 e la inversa h( x) 3 x
Le due curve sono simmetriche rispetto alla retta y=x
E si incontrano per x 3 x x( x 2 1) 0 nel primo quadrante per x=0 e per x=1
1
0
3
1
1
3
x
x31 1 3 43 x 4 1 3 1 1
x x dx
|0 x |0
1
4
4
4 4 2
1 3 1
3
3
4) Dato che g e la sua inversa son simmetrici rispetto a y=x considero la distanza massima dei punti
di g dalla retta y=x
| x y | | x x3 |
d
2
2
1
1
d'
(1 3x 2 ) da cui 1 3 x 2 0 x
3
2
d massima
3
27
3
3
27 2 3
9 4 32 6
2 3
9
2
2
9 2
Quindi la sezione massima ha area A 12
2 6 8 6
9
3
1
Il volume invece essendo un prisma si calcola aria di base per altezza. V 12 6
2
Quesito 1
( x a)2 a ( x a)2 b (b a)2 (b a)2
|b
|a
b
b
a
2
2
2
2
2
2
2
2
2
2
b
(b a) (b a)
b a 2ab b a 2ab
b2 a 2
b | x a |dx 2 2
2
2
b
a
b
| x a |dx ( x a)dx ( x a) |dx
Quesito 2
Di suriettive sì p.e.
Di iniettive no perché un elemento rimane sempre fuori. .
e quindi per definirlo deve avere un immagine già usata.
Di Biettive no perché A e B non hanno la stessa cardinalità
Quesito 3
Areamoneta
(l 2r )2 (100 2 12,875) 2
p
0,55 55%
Areamattonella
l2
1002
Quesito 4
Non puo esistere. Perché la somma delle facce deve essere minore di un angolo giro
Infatti , dato che un angolo di un esagono è 120°, se ne metto tre insieme ho 3*120=360 e quindi
non può essere minore di 360.
Quesito 5
Solo alla prima
0
0
1
0
1
in det er min ata
impossibile
0
0
00 e0ln 0 e0 forma indeterminata
Quesito 6
Applicando il metodo della tangente.
x
f
f'
N.
3 0,14112 -0,98999
3,142547 -0,00095
-1
3,141593 4,48E-10
-1
1
2
3
Ricordiamo che 3,1415926
Quesito 7
n n n k
(sviluppando sono il secondo membro ho che)
k 1 k k 1
n
n!
nk
n!
nk
n!
(k 1)!(n k 1)!
k 1 k ! n k ! k 1 (k 1)k ! n k (n k 1)! 1
Quesito 8
Ammettiamo che gli invitati siano n e che n1 uomini e n2 donne e quindi n n1 n2
Se xi è l’età di una persona per definizione ho
u1 u2 .. un1
In particolare se ui è l’età di un uomo per definizione ho che u
26
n1
d1 d 2 ... d n2
19
In particolare se d i è l’età di una donna per definizione ho che d
n2
x x ... xn (u1 u2 .. un1 ) (d1 d 2 .. d n2 )
m 1 2
22 da cui
n
n
n
26 1 19
26n1 19n2 26n1 19n2
26n1 19n2
n2
22
22 dividendo per n2
22
n1
n
n1 n2
n1 n2
1
n2
26r 19
3
22 26r 19 22r 22 r
r 1
4
Quesito 9
Il principio di cavalieri dice: “che se secando due solidi con piani paralleli, si ottengono aree uguali
allora i due volumi sono uguali.
Ad una distanza x dal vertice V ho la sezione del cono la cui area è data da
Abase _ cono
Acono x 2
Abase R 2
x2
x2
A
R2 x2
base
R2
R2
Abase _ Scodella Abase _ cono Acerchio _ cilindro r 2 (r 2 x2 ) x2
Dove il raggio nel secondo cerchio è VK r 2 x2
Quesito 10
Per il teorema delle rette parallele le due rette necessariamente si incontrano. Tale teorema si basa
sul quinto postulato, che per secoli è stato oggetto di discussioni, ed è stata cercata una
dimostrazione a partire dai 4 postulati. Non potendolo dimostrare il quinto postulato è stato negato,
ammettendo la possibilità di avere più rette parallele per un punto, e dando la possibilità di avere
geometrie non euclidee, dove la somma degli angoli di un triangolo non necessariamente è 180°