Compiti vacanze fisica
Classe 3^B 2008/2009 prof. Zenobi Antonella
Svolgere gli esercizi allegati, ripassando, per ciascun esercizio la teoria indicata.
Calcolo vettoriale:
1) Rappresenta in un piano cartesiano i vettori a 5i 2 j e b 3i 4 j . Determina per
componenti e in modulo a b , a b e a b e rappresentali.
2) Considera i tre vettori a 2 j , b 2i 2 j , c 4i e determina:
a) a b c ; a c ; b c ;
b) a b ; a b
c) (a b ) c
Legge oraria, spazio percorso, spostamento in un moto rettilineo
3) Due messaggeri A e B si devono incontrare per scambiarsi delle lettere. Entrambi partono a
cavallo a mezzogiorno dai loro castelli, collegati da una strada rettilinea lunga 30 km. Il
messaggero A corre alla velocità costante di 17 km/h, il messaggero B di 13 km/h. A che distanza
dal castello di A si incontrano? Dopo quanto tempo dalla partenza avviene l’incontro?
Rappresenta le leggi orarie dei due moti nello stesso piano cartesiano.
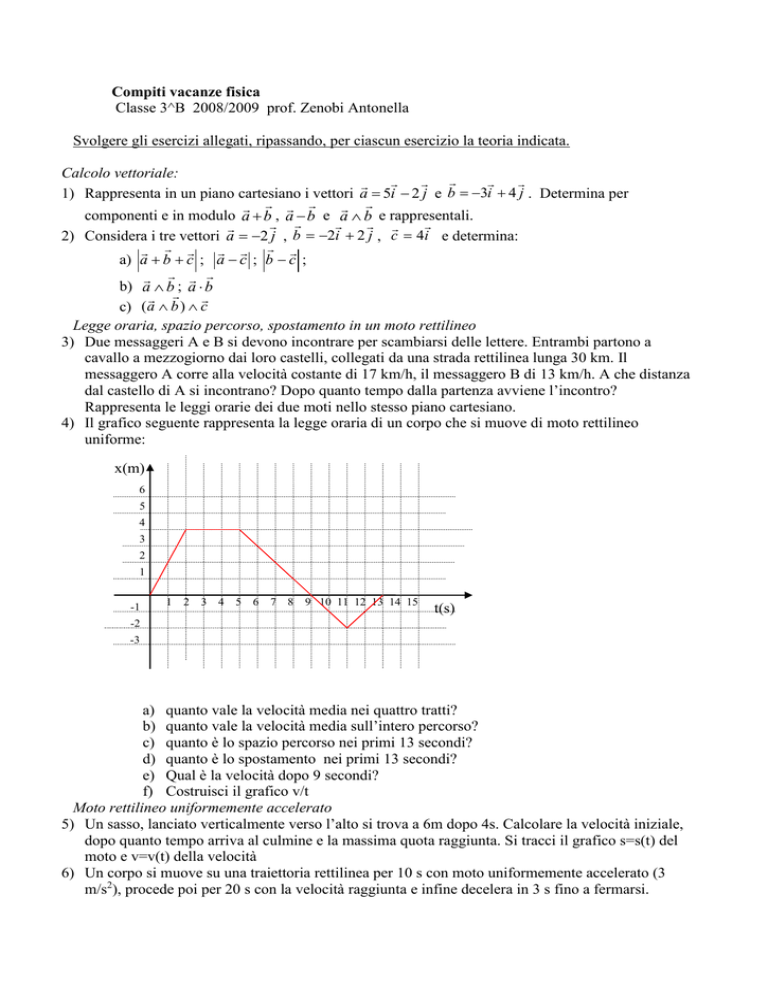
4) Il grafico seguente rappresenta la legge oraria di un corpo che si muove di moto rettilineo
uniforme:
x(m)
m)m6
m(m)
5
4
3
2
1
-1
1
2
3 4
5 6
7 8
9 10 11 12 13 14 15
t(s)
-2
-3
a) quanto vale la velocità media nei quattro tratti?
b) quanto vale la velocità media sull’intero percorso?
c) quanto è lo spazio percorso nei primi 13 secondi?
d) quanto è lo spostamento nei primi 13 secondi?
e) Qual è la velocità dopo 9 secondi?
f) Costruisci il grafico v/t
Moto rettilineo uniformemente accelerato
5) Un sasso, lanciato verticalmente verso l’alto si trova a 6m dopo 4s. Calcolare la velocità iniziale,
dopo quanto tempo arriva al culmine e la massima quota raggiunta. Si tracci il grafico s=s(t) del
moto e v=v(t) della velocità
6) Un corpo si muove su una traiettoria rettilinea per 10 s con moto uniformemente accelerato (3
m/s2), procede poi per 20 s con la velocità raggiunta e infine decelera in 3 s fino a fermarsi.
Disegnare i grafici velocità/tempo e spazio/tempo. Calcolare infine la velocità media sull’intero
moto.
7) Un’automobile A e un ciclista B viaggiano su una strada nello stesso verso. L’automobile segue il
ciclista. Quando la distanza è un km,A ha una velocità pari a v0A=36 Km/h, mentre B ha una
velocità pari a v0B=1 m/s e l’automobile comincia a decelerare. Il ciclista, invece, continua a
viaggiare con la sua velocità. Qual è il valore minimo del modulo della decelerazione affinché
l’automobile non urti il ciclista?
8) Un ragazzo sul tetto di una torre alta 60m lascia cadere liberamente un sasso, mentre un secondo
ragazzo alla base della torre lancia un altro sasso con velocità iniziale di 20 m/s. Calcolare:
a) dopo quanto tempo i due sassi si incontrano
b) a quale distanza dal suolo
c) la velocità del primo sasso all’istante dell’urto
d) la velocità del secondo all’istante dell’urto
e) Si tracci il grafico s=s(t) del moto e v=v(t) della velocità.
9) Dato il grafico v/t di un corpo che si muove di moto rettilineo:
v(m/s)
30
25
20
15
10
5
-5
-10
2
5
10
15
20
t(s)
-15
a) determinare lo spazio percorso dopo 10 s
b) determinare il suo spostamento rispetto all’origine dopo 20 s
c) determinare la sua accelerazione tra 5 e 10 s
d) ricavare il grafico s/t
10) I grafici v/t seguenti rappresentano i moti rettilinei di due corpi A e B. Nell’istante iniziale B vede
passare accanto a sé A. Analizzando il grafico ricavare il tempo impiegato da B per raggiungere A
e lo spazio percorso. Rappresentare i grafici s/t dei due moti sullo stesso piano cartesiano.
v(m/s)
6
B
5
4
3
A
2
1
-1
-2
-3
1
2 3 4 5
6 7 8 9 10 11 12 13 14 15
t(s)
composizione dei moti, moto parabolico, moto circolare uniforme, moto armonico semplice
11) Un aereo mentre scende in picchiata a 45° rispetto all’orizzontale lascia cadere una bomba da
un’altezza di 730 m. La bomba colpisce il suolo 5 s dopo il lancio.
a) Qual è la velocità dell’aereo?
b) Qual è lo spostamento orizzontale della bomba durante il volo?
c) Quali sono le componenti orizzontali e verticali della velocità della bomba un istante
prima che tocchi il suolo?
12) Un corpo si muove di moto circolare uniforme su una circonferenza di raggio R=2 m e impiega
un tempo t=12 s per fare mezzo giro. Determina:
a) velocità scalare media e vettoriale media nel primo quarto di giro;
b) velocità e accelerazione negli istanti t1= 6 s e t2=18 s.
c)come varierebbero la velocità scalare e il modulo dell’accelerazione se, sulla stessa traiettoria, il
corpo impiegasse 12 s per fare un giro completo?
13) Un ragazzo fa ruotare un sasso in un cerchio orizzontale a 2 m da terra mediante una corda lunga
1.5 m. La corda si spezza e la pietra schizza via orizzontalmente andando a colpire il terreno a 10
m di distanza. Quanto valeva l’accelerazione centripeta durante il moto circolare?
14) Un corpo si muove di moto armonico semplice secondo la seguente legge oraria: x 4 cos(3t 1)
espressa nel sistema M.K.S. Determina: pulsazione, periodo, velocità massima e accelerazione
massima.
principi della dinamica, reazione normale, forza peso, forza d’attrito
15) Una slitta di massa 24 kg si muove con velocità costante mentre viene tirata da una forza di 18 N
formante un angolo di 30° con l’orizzontale. Si determini il coefficiente d’attrito.
16) Un’auto che viaggia a 60 km/h frena bruscamente e riduce la propria velocità a 30 km/h in un
tempo pari a 2 s. Se la massa del passeggero è 65 kg, quanto vale la forza esercitata su di esso
dalla cintura di sicurezza?
17) Un corpo è scivola lungo un piano scabro, inclinato di un angolo di 30° rispetto all’orizzontale,
partendo dall’altezza h=2m con velocità iniziale vo=1 m/s. Il coefficiente di attrito dinamico tra il
piano e il corpo è kd=0,3. Si calcoli dopo quanto tempo il corpo raggiunge la base del piano e con
che velocità.
18) Un blocco di massa 3.8 kg è trascinato su un piano orizzontale privo di attrito da un altro blocco
di massa 0.5 kg collegato ad esso da un filo avvolto ad una carrucola e posto inizialmente a 3 m
da terra.Calcolare l’accelerazione del sistema, la tensione del filo e il tempo di caduta. Calcolare
l’accelerazione e la tensione nell’ipotesi che tra il primo blocco e il piano si eserciti attrito con
coefficiente k=0.2
19) Un pendolo è posto su un ascensore che sale con accelerazione costante di 1 m/s2. Calcolare il suo
periodo sapendo che la sua lunghezza è pari a 64 cm.
20) Due piani inclinati lunghi rispettivamente 1.2 m e 2 m sono posti uno accanto all’altro con
l’altezza in comune. I due blocchi A,posto sul primo piano, e B, posto sul secondo piano, sono
legati da una fune di massa trascurabile e sono in equilibrio. Determinare il peso del blocco B
sapendo che il blocco A pesa 1.5 N.
21)
Due masse m1=5 kg e m2=10 kg sono collegate come in figura . Il piano
inclinato di 30° è scabro con coefficiente di attrito dinamico kd=0,3. Sapendo
che la massa m2 si muove verso il basso,determina l’accelerazione del sistema m1
e la tensione della fune.
22) Un piano inclinato di un angolo =30° rispetto all’orizzontale è fissato
su un carrello e sul piano è poggiato un blocco (vedi figura). Quanto deve
valere l’accelerazione del carrello (e quindi del piano inclinato) affinché il
blocco rimanga in quiete rispetto al piano inclinato?
m2