Corso di Fisica tecnica ambientale e Impianti tecnici – a.a. 2008/2009
CAPITOLO 4
CONTROLLO DELLA RADIAZIONE SOLARE
La localizzazione e l’orientamento di un edificio per ridurre l’esposizione solare
estiva e valorizzare quella invernale, sono obiettivi fondamentali per una corretta
progettazione. Esistono, a tal riguardo, diversi strumenti di calcolo e metodi grafici per
visualizzare il soleggiamento su edifici/pareti.
4.1
Meridiana orizzontale
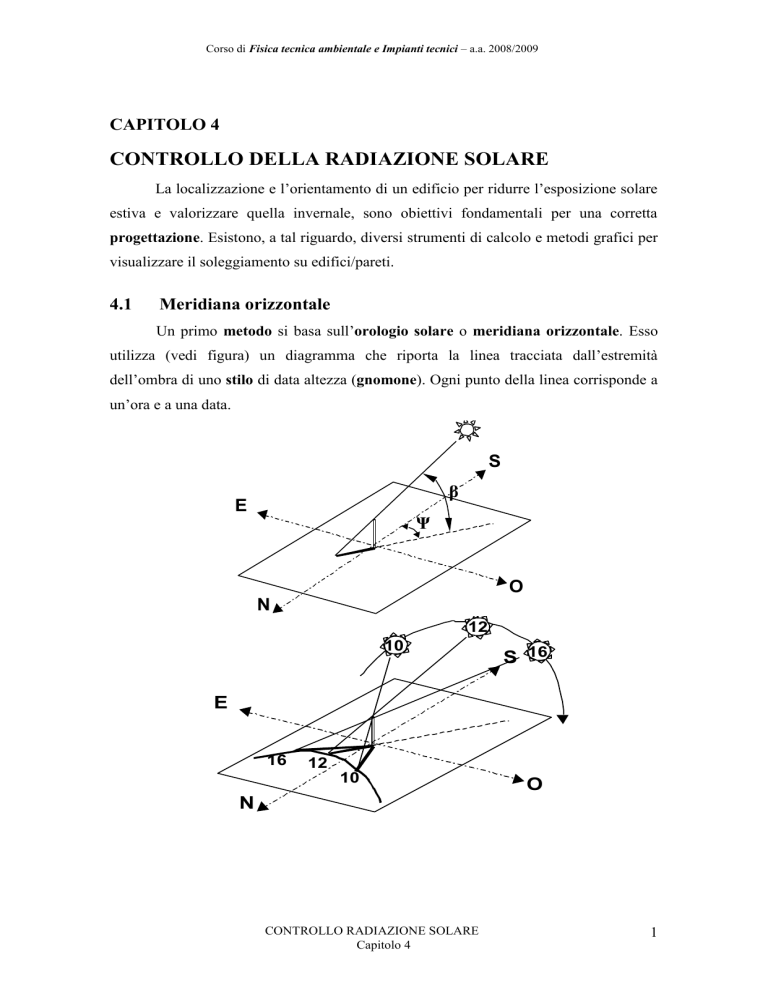
Un primo metodo si basa sull’orologio solare o meridiana orizzontale. Esso
utilizza (vedi figura) un diagramma che riporta la linea tracciata dall’estremità
dell’ombra di uno stilo di data altezza (gnomone). Ogni punto della linea corrisponde a
un’ora e a una data.
S
β
E
Ψ
O
N
12
10
S 16
E
16
12
10
O
N
CONTROLLO RADIAZIONE SOLARE
Capitolo 4
1
Corso di Fisica tecnica ambientale e Impianti tecnici – a.a. 2008/2009
Prefissati latitudine, altezza dello gnomone e riferendosi all’uindicesimo giorno
di ogni mese si può ottenere una figura del tipo sotto rappresentato:
N
dic
dic
nov
gen
feb
ott
set
mar
O
E
ago
lug
giu
7
17
6
18
altezza gnomone = 1 cm
apr
mag
giu
S
LAT. 36 °N
L’utilizzo di questo metodo presuppone un modello in scala dell’edificio e degli
eventuali ostacoli circostanti. La procedura, illustrata nella seguente figura, prevede di
porre il modello in scala dell’edificio su una tavola inclinabile ed orientabile su cui si
incolla, orientata con la direzione Nord-Sud, la meridiana. A questo punto si posiziona
sulla meridiana il relativo gnomone e si espone
l’insieme al sole regolando
inclinazione ed orientamento del tavolo in modo da far sì che l’ombra dello gnomone
indichi l’ora ed il mese di interesse.
Una fotografia potrà documentare la situazione di esposizione o di ombra delle
varie parti dell’edificio. In laboratorio si potrà ricorrere alla stessa procedura solo se si
dispone di un sistema ottico atto a realizzare un fascio di luce con radiazioni
sufficientemente parallele e non divergenti.
CONTROLLO RADIAZIONE SOLARE
Capitolo 4
2
Corso di Fisica tecnica ambientale e Impianti tecnici – a.a. 2008/2009
4.2 Carta dei percorsi solari
Come si è già osservato, un volta che sia prefissata la latitudine di una località si
può facilmente costruire la relativa carta dei percorsi solari (diagrammi polari che
riportano l’andamento degli angoli solari (altezza ed azimut Ψ ) durante il giorno
nei vari mesi dell’anno.
N
O
Giu
Lug 19
18
Ago
17
16
90
1514
9
Set
13 1110
150
6
5 Giu
Mag
Apr
90
Mar
7
8
150
0
10
20
30
40
50
60
70
80
Ott
Nov
Dic
E
Feb
Gen
Dic
30
30
0
S
Queste carte sono anche molto utili per poter individuare facilmente i mesi in cui
una data superficie “vedrà o non vedrà” il sole tenendo conto delle ombre su di essa
proiettate da altri manufatti, alberi, rilievi, etc. A questo scopo si può iniziare ad
osservare che una superficie verticale (ad es. una parete) “vede” sempre, prescindendo
da eventuali altri ostacoli, solo metà del cielo, ovvero un emisfero; ad esempio nella
figura seguente una parete esposta a Nord (per una latitudine di 44°) maschera metà
del cielo sovrastante (parte grigia in figura).
CONTROLLO RADIAZIONE SOLARE
Capitolo 4
3
Corso di Fisica tecnica ambientale e Impianti tecnici – a.a. 2008/2009
N
19
18
17
16
1514
9
13 1110
90
O
150
5
6
7
90
8
150
0
10
20
30
40
50
60
70
80
E
60
30
60
30
30
30
S
0
Si può notare che la parete sarà soleggiata soltanto d’estate e nelle ore prossime all’alba
ed al tramonto. Per quanto riguarda le ombre proiettate in un punto P da altri edifici,
alberi, ecc., il procedimento risulta assai semplice. Si consideri, ad esempio, il caso di
un albero.
1
P
2
Ψ
Ψ
Ψ
3
2
1
P
3
P
Il punto P “non vedrà” il Sole a causa dell’albero quando questo sarà nella
regione del cielo limitata in pianta dagli angoli Ψ1, Ψ3, ed in elevazione , 3 come
rappresentato schematicamente in pianta e in sezione nella figura.
CONTROLLO RADIAZIONE SOLARE
Capitolo 4
4
Corso di Fisica tecnica ambientale e Impianti tecnici – a.a. 2008/2009
Riportando i vari angoli sul diagramma relativo alla latitudine del luogo, si può
determinare quando l’albero farà ombra nel punto P.
N
O
Giu
Lug 19
18
17
Ago
16
90
1514
9
Set
13 1110
150
6
5 Giu
Mag
7
8
150
0
10
20
30
40
50
60
70
80
Ott
Nov
Dic
Apr
90
Mar
E
Feb
Gen
Dic
30
30
0
S
CONTROLLO RADIAZIONE SOLARE
Capitolo 4
5
Corso di Fisica tecnica ambientale e Impianti tecnici – a.a. 2008/2009
4.3 Ombre da protezioni solari verticali ed orizzontali
Un elemento verticale o orizzontale posto a lato o sopra un osservatore intercetta
una parte di cielo e se il Sole si trova nella parte intercettata l’osservatore sarà in ombra.
Un segmento verticale di lunghezza finita visto dall’osservatore può essere proiettato
sulla sfera celeste come un arco di cerchio; la posizione dell’arco è individuabile sul
diagramma polare mediante l’angolo formato con la direzione di riferimento (Sud) e
con l’angolo sotteso dall’arco stesso rispetto al piano orizzontale, come rappresentato
sulla parte alta della seguente figura.
14131110
Se s’immagina ora di tracciare sopra l’osservatore (parte bassa della figura) una
serie di segmenti orizzontali paralleli, le loro proiezioni sulla sfera celeste la
suddividono in curve (meridiani), distanziate di un angolo determinato dalla distanza tra
le linee. Ipotizzando di tracciare una doppia serie di meridiani perpendicolari tra loro e
di trasferire le relative proiezioni sulla sfera celeste su diagramma polare si ottiene il
diagramma di seguito riportato (regolo graduato), in cui è considerata solo metà della
volta celeste, essendo l’altra identicamente simmetrica.
CONTROLLO RADIAZIONE SOLARE
Capitolo 4
6
Corso di Fisica tecnica ambientale e Impianti tecnici – a.a. 2008/2009
N
0
150
20
150
40
60
O
80
90
90
14 13 80
1110
E
60
60
60
30
40
20
30
30
30
0
S
Vediamo ora alcuni casi di ombre portate da aggetti (esposizione parete Sud).
Aggetto orizzontale di dimensioni finite su superficie vetrata.
E’ necessario:
1. valutare l’ampiezza degli angoli formati dalle congiungenti il punto d’osservazione
P (base della finestra) con le estremità dell’aggetto.
40 °
60 °
P
2. riportare tali angoli sul regolo graduato.
Nella figura sono disegnate (in rosso) le curve relative ad aggetti orizzontali che
determinano compresi tra 90° (assenza di aggetto) a 0° (aggetto indefinitamente
sporgente), variabili di 10° in 10°.
CONTROLLO RADIAZIONE SOLARE
Capitolo 4
7
Corso di Fisica tecnica ambientale e Impianti tecnici – a.a. 2008/2009
60°
40°
1
14
3
1
11
0
S
Ad esempio, la curva = 60° si riferirà ad un aggetto con sporgenza s. Risulta valere la
relazione h/s = arctan ove h rappresenta la distanza dell’aggetto rispetto al punto P.
Identicamente le linee blu definiscono la variabilità dell’angolo (0 – 90°).
3. sovrapporre al diagramma percorsi solari la maschera correttamente orientato.
8
150
20
30
40
Giu
50
Lug 19
60
18
70
17
80
16
15
14 13 1110 9
Ago
90
Set
Ott
Nov
Dic
30
0
S
6
150
7
30
5 Giu
Mag
Apr
90
Mar
Feb
Gen
Dic
E
In figura la maschera orientata a Sud è sovrapposta al diagramma dei percorsi
solari. Si può facilmente individuare i periodi dell’anno in cui il punto P e, quindi, la
superficie vetrata è ombreggiata dalla schermo orizzontale.
CONTROLLO RADIAZIONE SOLARE
Capitolo 4
8
Corso di Fisica tecnica ambientale e Impianti tecnici – a.a. 2008/2009
Aggetto orizzontale di dimensioni infinite (angolo tendente a zero).
Rappresenta il caso limite dell’aggetto orizzontale di dimensioni finite.
60°
volta
celeste
s ostrui ta
14131110
volta
celeste
visibile
S
h
Aggetto verticale di dimensioni finite
60°
60°
14 13 1110
50°
50°
CONTROLLO RADIAZIONE SOLARE
Capitolo 4
9
Corso di Fisica tecnica ambientale e Impianti tecnici – a.a. 2008/2009
Aggetto verticale di dimensioni infinite
60°
60°
14 13 1110
Sul regolo graduato si possono disegnare le maschere caratteristiche di diversi
tipi di protezione solare. Si noti che queste maschere non dipendono né dalla
orientazione della facciata, né dalla latitudine.
Si può precisare ancora che è la geometria angolare e non la dimensione fisica
della protezione che determina la maschera dell’ostruzione, ad esempio un grande
aggetto orizzontale e una serie di lamelle pure orizzontali e con lo stesso angolo di fuga
generano la stessa maschera.
CONTROLLO RADIAZIONE SOLARE
Capitolo 4
10
Corso di Fisica tecnica ambientale e Impianti tecnici – a.a. 2008/2009
Nella seguente figura sono riportate le maschere di alcune tra le più comuni soluzioni
progettuali.
CONTROLLO RADIAZIONE SOLARE
Capitolo 4
11
Corso di Fisica tecnica ambientale e Impianti tecnici – a.a. 2008/2009
ESERCIZI ED ESEMPI
1) Si consideri qualitativamente il caso di una finestra orientata a Sud Ovest e dotata di
schermature verticali e orizzontali come rappresentato in figura.
arctg s/h
Per determinare in quali periodi dell’anno la finestra sia in ombra è sufficiente
costruire la maschera caratteristica della geometria di schermatura ipotizzata. Gli aggetti
verticali ed orizzontali posti a protezione della finestra sono sovrapposti al diagramma
dei percorsi solari orientato in accordo con l’esposizione della parete (Sud Ovest)
come rappresentato nella seguente figura.
CONTROLLO RADIAZIONE SOLARE
Capitolo 4
12
30
N
S
O
No tt
v
Di
c
0
Ag
o
90
Se
t
30
14
16
15
17
19
18
Lu G
g iu
13
11 1
0
CONTROLLO RADIAZIONE SOLARE
Capitolo 4
50
7
Fe
40
30
Di Ge b
c n
60
9
7
80 0
15
0
8
O
E
M
ar
20
5
S
15
0
O
E
G
M iu
ag
Ap
90 r
0
6
10
N
Corso di Fisica tecnica ambientale e Impianti tecnici – a.a. 2008/2009
13