Esercizio sugli scambiatori di calore

Tagliati Alessandro – matricola 118042 – lezione del 24/01/2000 – ore 8:30 – 10:30
Scambiatori di Calore
Gli scambiatori di calore, sono apparecchiature utilizzati al fine di favorire il trasferimento di
energia (sotto forma di calore) tra due fluidi a temperature diverse. Possiamo schematizzare uno
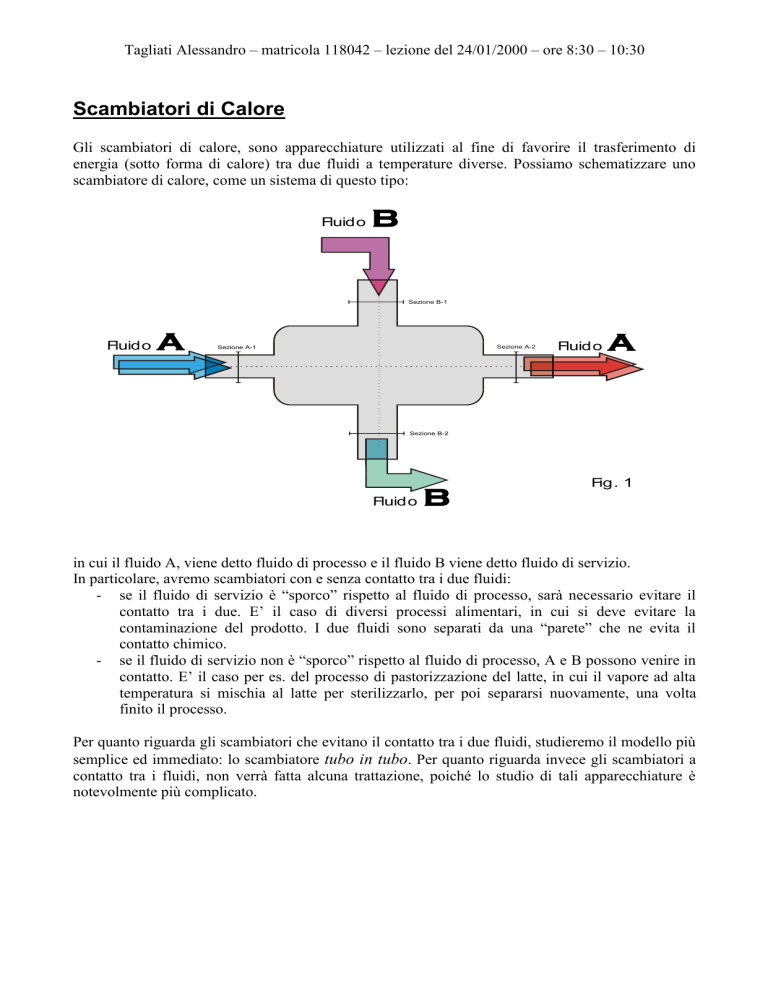
scambiatore di calore, come un sistema di questo tipo:
Fluido
B
Sezione B-1
Fluido
A
Sezione A-2
Sezione A-1
Fluido
A
Sezione B-2
Fluido
B
Fig. 1
in cui il fluido A, viene detto fluido di processo e il fluido B viene detto fluido di servizio.
In particolare, avremo scambiatori con e senza contatto tra i due fluidi:
- se il fluido di servizio è “sporco” rispetto al fluido di processo, sarà necessario evitare il
contatto tra i due. E’ il caso di diversi processi alimentari, in cui si deve evitare la
contaminazione del prodotto. I due fluidi sono separati da una “parete” che ne evita il
contatto chimico.
- se il fluido di servizio non è “sporco” rispetto al fluido di processo, A e B possono venire in
contatto. E’ il caso per es. del processo di pastorizzazione del latte, in cui il vapore ad alta
temperatura si mischia al latte per sterilizzarlo, per poi separarsi nuovamente, una volta
finito il processo.
Per quanto riguarda gli scambiatori che evitano il contatto tra i due fluidi, studieremo il modello più
semplice ed immediato: lo scambiatore tubo in tubo. Per quanto riguarda invece gli scambiatori a
contatto tra i fluidi, non verrà fatta alcuna trattazione, poiché lo studio di tali apparecchiature è
notevolmente più complicato.
Tagliati Alessandro – matricola 118042 – lezione del 24/01/2000 – ore 8:30 – 10:30
Scambiatori di calore Tubo-in-Tubo
Sono costituiti da due tubi concentrici, in cui passano due fluidi a temperature diverse. Possiamo
schematizzare questa apparecchiatura in questo modo:
Scambiatore TUBO-in-TUBO
(m odello equic orrente)
Tubo c onduttore
Tubo esterno
Fluido B
Sezione B-1
Sezione A-2
r2
Sezione A-1
Calore scambiato
Fluido A
x
0
x
x+ x
r1
Sezione B-2
L
X
Fig. 2
Il tubo interno dovrà essere fatto con materiali ad alta conducibilità termica, per consentire uno
scambio più alto possibile di calore tra i due fluidi: si userà quindi in generale un metallo ad
altissima conducibilità, per es. l’acciaio che offre inoltre un’alta resistenza all’usura. In particolare
con l’acciaio inox (lucidato) diventa particolarmente semplice anche la pulizia della parte interna
del tubo (in cui passa il fluido A), diventando particolarmente indicato nei settori in cui l’igiene è un
fattore determinante (industria alimentare). Per quanto riguarda il tubo esterno, non si ha alcuna
necessità perché questo sia fortemente conduttivo, per cui si useranno metalli a bassa conducibilità
termica (anche se non necessariamente un isolante). Nel nostro caso lo considereremo isolante:
questo ci permetterà di non considerare perdite all’esterno nello scambio energetico.
Questo tipo di scambiatore, presenta un’estrema facilità di calcolo per quanto riguarda il
dimensionamento delle superfici di scambio e della quantità di calore scambiato, per cui ne permette
il calcolo esatto delle caratteristiche. Tuttavia risulta essere molto costoso (acciaio inox lucidato) ed
ingombrante rispetto alla potenza termica dissipata. E’ quindi vantaggioso solo in quei settori in cui
è necessaria un’estrema pulizia (settore alimentare e farmaceutico) ed affidabilità, e in cui il valore
aggiunto del prodotto copra in breve termine il costo dell’impianto.
Tagliati Alessandro – matricola 118042 – lezione del 24/01/2000 – ore 8:30 – 10:30
A seconda che il fluido B sia entrante o uscente dalla sezione B-1 (considerando il verso positivo
dell’asse X come indicato in Fig. 2), avremo scambiatori detti in Equicorrente (ovvero A e B hanno
lo stesso verso di percorrenza dei tubi) oppure in Controcorrente (ovvero B scorre in verso opposto
ad A: entra alla sezione B-2 ed esce alla sezione B-1). Come vedremo ognuna delle due soluzioni,
presenterà caratteristiche diverse ed utili ad applicazioni diverse.
Per quanto riguarda il calcolo degli scambiatori, occorre distinguere il
Calcolo termico
(dimensionamento delle superfici di scambio)
T
Q 
RTot
(1)
Calcolo energetico
(relazioni del I° principio della
termodinamica)
Q  M A  CPA  (TA2  TA1 )
Q  M B  CPB  (TB2  TB1 )
(2)
(3)
(nel calcolo energetico, consideriamo la pressione praticamente costante, ovvero liquidi
incomprimibili).
Mentre il calcolo energetico è dato semplicemente dal bilancio dell’entalpia (tanto calore cede un
fluido, tanto l’altro ne riceve), il calcolo termico è più articolato (si devono calcolare le resistenze
termiche, i coefficienti di convezione e il funzionamento delle superfici di scambio).
Consideriamo uno scambiatore in equicorrente, in cui il fluido A è a temperatura di ingresso al
sistema, più bassa del fluido B, e analizziamo il tratto di lunghezza L, tra la sezione A1 e A2, come
mostrato in Fig. 1. Avremo, in un diagramma che lega la temperatura alla distanza dall’ingresso del
sistema, una situazione di questo tipo:
T
Fig. 3
sezione 1
sezione 2
0
x x+ x
L
X
Tagliati Alessandro – matricola 118042 – lezione del 24/01/2000 – ore 8:30 – 10:30
Notiamo un T variabile, ovvero avremo un flusso termico fortemente variabile: in particolare, alla
sezione 1, essendoci un T=T1 grande, il flusso termico tra i due fluidi sarà piuttosto vivace,
mentre alla sezione 2, poiché il T=T2 è molto basso, il flusso termico sarà quasi nullo.
Data la natura così variabile di T, siamo costretti, nello studio della potenza scambiata Q , a
considerare in realtà un Q (il suo valore medio), e di conseguenza un T medio.
Consideriamo uno “scambiatore” infinitesimo di lunghezza δx, all’interno del quale possiamo
ritenere l’andamento di ΔT praticamente lineare. Ottengo quindi una relazione, alla coordinata x:
Q 
TB ( x)  TA ( x)
RTot
(4)
in cui RTot rappresenta la resistenza termica dello scambiatore infinitesimo e che possiamo
rappresentare in questo modo:
Convezione interna
del fluido A
Conduzione del
tubo interno
Convezione esterna
al tubo interno
(del fluido B)
1
hi  2    r1  L
ln
r2
r1
1
he  2    r2  L
Fig. 4
in cui: λ è la conducibilità termica del materiale con il quale è costruito il tubo interno,
hi è il coefficiente di convezione interno,
he è il coefficiente di convezione esterno,
L è la lunghezza dello scambiatore considerato, in questo caso δx.
La resistenza totale RTot è la somma dei tre termini (poiché la lunghezza dello scambiatore è
infinitesima, si ottiene rapidamente che la resistenza termica risulta infinita).
Definiamo ora il coefficiente globale di scambio K in relazione alla superficie di scambio S come:
2    r1  L
(5)
1 r1
r2
r1
  ln 
hi 
r1 he  r2
in cui K è strettamente legata alla superficie in cui avviene lo scambio S.
K S 
Possiamo quindi scrivere la RTot per unità di superficie come:
RTot 
1
K S
(6)
per cui otteniamo:
(7)
Q  K  S  T

e conseguentemente:
(8)
Q  K  2    r1  x  TB  TA 
ovvero il Q (che è un infinitesimo: compare infatti il δx a numeratore) in funzione di [TB-TA] .
Tagliati Alessandro – matricola 118042 – lezione del 24/01/2000 – ore 8:30 – 10:30
Esprimiamo ora il Q , anche attraverso le relazioni energetiche date dalle formule (2) e (3):
Q  M A  CPA  TA
(9)
 
Q  M B  CPB  TB
da cui otteniamo:

Q
TA  
M A  C PA



TB  Q

M B  C PB
(10)


1
1




 M B  CPB M A  CPA 
ovvero, facendo la differenza tra i due termini:
TA  TB   Q  
e per le proprietà della derivata :
 TA  TB   Q   


 M B  CP M A  CP 

1

1
B
(11)
(12)
A
in cui compare ancora il termine [TB-TA].
Sostituendo nell’equazione (8), la relazione (12) ora trovata, otteniamo:
 TB  TA   K  2   r1  x  TB  TA 
(13)
ovvero un’equazione differenziale a variabili separabili:
 1

 TB  TA 
1
  K  2  r1  x  


TB  TA
 M A  CPA M B  CPB 
(14)
Integrando il primo membro tra la sezione 1 e la sezione 2, e il secondo membro su tutta la
lunghezza dello scambiatore, tra 0 ed L, otteniamo:
 1

TB  TA2
1
(15)
ln 2
  K  2


x  L   


TB1  TA1
 M A  CPA M B  CPB 
S
Poiché però si vuole arrivare ad un’espressione del tipo:
ricaviamo il termine K  S dall’equazione (15):
TB  TA2
ln 2
TB1  TA1
K S  
1
1

M A  C PA M B  C PB
Q  K  S  T
Dalle espressioni (2) e (3), si può facilmente ricavare:
TA  TA
TB  TB
1
1
e
 2  1
 2  1
M A  CPA
Q
M B  CPB
Q
(16)
(17)
(18)
per cui la (17) diventa:
 TB2  TA2 
ln
  Q
 TB1  TA1 
K S   
(TB1  TA1 )  (TB2  TA2 )
(19)
Tagliati Alessandro – matricola 118042 – lezione del 24/01/2000 – ore 8:30 – 10:30
ln
Sostituendo in (16) : Q  Q  T 
TB1  TA1
TB2  TA2
(20)
(TB1  TA1 )  (TB2  TA2 )
ovvero l’espressione che cercavamo per il T che sarà quindi un T medio logaritmico:
T1  T2
(21)
T1
ln
T2
in cui i vari Tn rappresentano le differenze di temperatura tra i due fluidi, all’entrata e all’uscita del
sistema.
TL 
Notiamo che nello sviluppo del modello di TL le uniche ipotesi che si sono fatte sono la
incomprimibilità dei due fluidi: siamo infatti arrivati ad un’espressione in cui compaiono solo le
differenze di temperatura dei due fluidi alle due sezioni dello scambiatore.
Consideriamo ora uno scambiatore in controcorrente, schematizzabile in questo modo:
Scambiatore TUBO-in-TUBO
(m odello c ontroc orrente)
Fluido B
Sezione B-1
Tubo c onduttore
Tubo esterno
Sezione A-2
Sezione A-1
Fluido A
Sezione B-2
0
L
X
Fig. 4
Tagliati Alessandro – matricola 118042 – lezione del 24/01/2000 – ore 8:30 – 10:30
poiché l’entrata del fluido B avverrà alla sezione 2, dove invece il fluido A esce, avremo una
situazione di questo tipo:
T
Fig. 5
sezione 2
sezione 1
0
x x+ x
L
X
in cui notiamo che il ΔT rimane lungo tutto il tragitto, quasi costante, variando poco tra 0 ed L.
Passando al calcolo del T , possiamo, date le considerazioni fatte, utilizzare l’espressione del TL
trovato in (21).
Negli scambiatori di calore in controcorrente, avremo, a parità delle quattro temperature di ingresso
ed uscita dei due fluidi, un TL maggiore rispetto agli scambiatori di calore in equicorrente:
TL,CC  TL,EC
(22)
Questo, dalla (16) (K non è influenzato dalla corrente dei fluidi e Q CC  Q EC ) si traduce nella
minore necessità, da parte degli scambiatori in controcorrente, di superficie di scambio, e cioè è
possibile costruire scambiatori meno ingombranti (e di conseguenza avere minori costi di materiale,
dato che l’acciaio lucidato ha elevati costi).
Si deve però considerare la bassa variazione di ΔT lungo il percorso: se da un punto di vista
termodinamico questo potrebbe sembrare un vantaggio (poca perdita di energia), dal punto di vista
dello scambio termico, questo significa avere uno scambio meno vivace, ovvero una maggiore
lentezza nel cambiamento di temperatura del fluido di processo. Negli scambiatori in equicorrente,
il forte ΔT iniziale, consente un brusco cambio di temperatura iniziale del fluido A, portandolo
subito ad una temperatura più bassa [alta] in breve tempo.
In situazioni critiche (dove cioè si deve interrompere velocemente un processo termico, per es. per
interrompere un processo di pastorizzazione) si useranno più scambiatori in serie: il primo sarà uno
scambiatore in equicorrente per cambiare rapidamente la temperatura del fluido A, gli altri in
controcorrente, in modo da ridurre spazio e quindi costi.
Tagliati Alessandro – matricola 118042 – lezione del 24/01/2000 – ore 8:30 – 10:30
Esercizio sugli scambiatori di calore
Si deve raffreddare dell’azoto con dell’acqua, attraverso uno scambiatore di calore tubo in tubo.
kg
L’azoto ha una portata M N2  1200
e parte da una temperatura iniziale TN2 ,1  200C , per
h
passare poi ad una temperatura di uscita pari a TN 2 , 2  50C .
kg
L’acqua ha una portata M H 2 0  5000
e una temperatura iniziale TH 2 O ,1  20C .
h
 Determinare la temperatura dell’acqua in uscita TH 2O , 2  20C .

Supponendo che la pressione dell’N2 sia PN2  2 bar  cost , calcolare la lunghezza L dello
scambiatore, sia nel caso equicorrente, che nel caso controcorrente.
Lo scambiatore è dimensionato:
Tubo c onduttore
Tubo esterno
Di,2
Di,1
De,1
0
X
L
in cui: il diametro interno del tubo conduttore misura  Di,1 =101 mm
il diametro esterno del tubo conduttore misura  De,1=108 mm
il diametro interno del tubo esterno misura
 Di,2 =125 mm
I° Punto:
La temperatura dell’acqua in uscita dal sistema può essere facilmente calcolata utilizzando le
relazioni del bilancio di energia. Sappiamo infatti che la potenza termica dissipata dall’azoto, deve
essere bilanciata da un assorbimento da parte dell’acqua di un’analoga quantità di energia:
Q
 M
 C  (T
T
)  Q
H 2O
e
H 2O
PH 2O
H 2O ,1
H 2O , 2
Q N2  M N2  CPN  (T N2 ,1TN2 , 2 ) 
2
N2
1200
3600



1,04  (200  50)  52
kW
s
convertitoal secondo
Sostituendo otteniamo:
TH 2O , 2  TH 2O ,1 
Q N2
M H 2O  C PH O
2
 20 
52
 29C
5000
 4,187
3600
Tagliati Alessandro – matricola 118042 – lezione del 24/01/2000 – ore 8:30 – 10:30
II° Punto:
Per la soluzione dovrò usare la relazione Q  K  S  T prima nel caso in equicorrente, e poi nel
caso controcorrente. Calcoliamo i due TL,CC e TL,EC :
(200  20)  (50  29)
 74C
200  20
ln
50  29
(200  29)  (50  20)

 81C
200  29
ln
50  20
TL ,EC 
TL ,CC
Per il calcolo del coefficiente di scambio :
K
1
r
r
r 1
1
 i ,1  ln e ,1  i ,1 
hi

ri ,1 re , 2 he
acciaio
è necessario ricavare prima i coefficienti di convezione.
- lato azoto:
l’azoto entra ad una temperatura di 200°C ed esce a 50°C  consideriamo una temperatura
media pari a 125°C=398K.
Poiché conosciamo il valore di pressione dell’azoto, dalla relazione dei gas perfetti,
ricaviamo la densità:
P
200000
kg
N2 

 1,6 2
R  T 297  398
m
grazie alla quale posso trovare la velocità alla parete:
1200
M N2
m
3600
WN2 

 24,6

 N2 
A
s

1,6  0,1012 
area della parete
4
Posso quindi calcolare il n° di Reynolds:
 N WN2  D
Re  2
 193000
N
2
dal cui valore sappiamo che l’azoto è in regime molto turbolento.
Per ricavare quindi il nostro coefficiente di convezione interna hi dobbiamo ricorrere al
numero di Nüsselt secondo l'equazione di Dittus-Boelter che ha validità per i fluidi correnti
in tubo in regime turbolento:
Nü  N2
W
hi 
 110,6 2

Nü  0,023  Re 0,8  Pr 0,3  351,2
Di,1
m K
-
lato acqua:
dobbiamo ripetere le stesse operazioni, con la differenza che la densità dell’acqua, ritenuta
kg
incomprimibile, sarà  H 2O  1000 2 e dovremo calcolare il diametro equivalente della
m
corona circolare in cui scorre l’acqua.


2
2
Area della corona  A   Di , 2   De,1  0,0031m 2
4
4
Tagliati Alessandro – matricola 118042 – lezione del 24/01/2000 – ore 8:30 – 10:30
4 A
4 A

 0,017m
Perimetro   Di , 2  De,1 
Calcoliamo quindi la velocità dell’acqua:
5000
M H 2O
m
3600
WH 2O 

 0,45
 H2O  A 1000  0,0031
s
Diametro equivalente  D 
e quindi il n° di Reynolds:
Re 
D


1000  0,017
 8500
0,9 106
vis cos ità cinematica
Poiché il n° di Reynolds è inferiore a 10000, non possiamo utilizzare le relazioni di Dittus e
Boelter per trovare il n° di Nüsselt, ma dovrò usare la formula di Böhm:
Nü  0,0033  Re  Pr 0,37  0,0033  8500  6,10,37  54,8
Ottengo quindi un coefficiente di convezione he 
Nü  H2O
D
Posso calcolare il coefficiente di scambio, che risulta K  104,5
 1956
W
m2 K
W
m2 K
kW
 K    Di  L  T
Ricordando che la potenza scambiata era Q  52



s
S
Q
ottengo una lunghezza L 
in cui non resta che sostituire il valore di T nei due casi
K    Di  T
da considerare:
Q
5200

 21,19m
K    Di  TEC 104,5    0,101  74
Q
5200


 19,36m
K    Di  TCC 104,5    0,101  81
LEC 
LCC
Come ci aspettavamo, il modello in controcorrente è più corto del modello in equicorrente.