Prova scritta di Misure Elettriche NO del 7 giugno 2016
1. Trovare la misura del volume di un cilindro utilizzando un calibro con accuratezza dichiarata dell’1% con cui si
riportano le seguenti 5 letture in millimetri dell’altezza, h, e 6 letture del diametro di base, d:
hi
di
171.05
23.10
171.15
23.15
171.10
23.05
171.20
23.20
171.15
23.15
23.10
Dopo avere illustrato le quattro ipotesi alla base della propagazione delle incertezze nel modello probabilistico
prendere in esame il caso in cui le grandezze siano correlate, ma solo dal punto di vista teorico.
2. Dopo avere descritto lo schema costruttivo e tutto quello che sapete su un amperometro elettromeccanico a bobina
mobile progettare utilizzando questo strumento (schema circuitale e dimensionamento delle resistenze di shunt) un
voltmetro a tre portate di 1V, 5 V e 10 V con corrente di fondo scala I fs 1 mA e resistenza interna RG=(1 k 1)
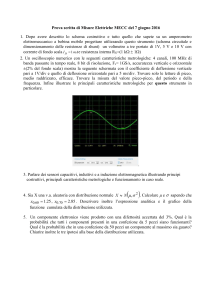
3. Un oscilloscopio numerico con le seguenti caratteristiche metrologiche: 4 canali, 100 MHz di banda passante in
tempo reale, 8 bit di risoluzione, Fc= 1GS/s, accuratezza verticale e orizzontale (2% del fondo scala) mostra la
seguente schermata con il coefficiente di deflessione verticale pari a 1V/div e quello di deflessione orizzontale pari a
5 ms/div. Trovare solo le letture di picco, medio raddrizzato, efficace. Trovare la misura del valore picco-picco, del
periodo e della frequenza. Infine illustrare le principali caratteristiche metrologiche per questo strumento in
particolare.
.
4. Parlare dei sensori capacitivi, induttivi e a induzione elettromagnetica illustrando principi costruttivi, principali
caratteristiche metrologiche e funzionamento in caso reale.
1. Secondo il MIUR negli A.A. dal 1996 al 2004 gli immatricolati ad Ingegneria delle Università italiane sono stati:
39155, 37863, 35381, 34885, 37061, 37178, 37193, 36864. Si assuma che il numero X di immatricolati annuali ad
Ingegneria sia distribuito normalmente. Calcolare un intervallo di confidenza al 90% e al 95% per il valore atteso di
X.
2. Supponiamo che un farmaco sia ritenuto efficace se provoca la guarigione nell’80% dei casi. In una sperimentazione
clinica 143 pazienti sono stati curati con un nuovo farmaco e 121 di essi sono guariti. Si può affermare che il nuovo
farmaco sia efficace? (Suggerimento: se p = ”probabilità che un paziente curato con il nuovo farmaco guarisca” H0:
p 0.80). Fare il grafico e se possibile trovare il p-value del test. Commentare i risultati ottenuti al livello del 5% e
del 10%.
3. Per verificare se un nuovo farmaco antidepressivo abbia effetto, 60 pazienti sono suddivisi a caso in due gruppi da
30. Quelli del primo gruppo vengono curati con il farmaco mentre a quelli del secondo gruppo è somministrato un
placebo:
presente
assente
cura
effetto
19
11
con il farmaco
14
16
con il placebo
E’ possibile, aiutandosi con un grafico, concludere che quel farmaco abbia un qualche effetto nel trattamento della
malattia?