Un conduttore sferico A di raggio R1=40 cm e` posto al centro di una

Primo compito di esonero di Elettricita’ e Magnetismo A. A. 2002-2003
(Proff. B. Borgia, A. Frova, G. Marini)
17 Febbraio 2003
Nello svolgimento del compito dare priorità al primo esercizio
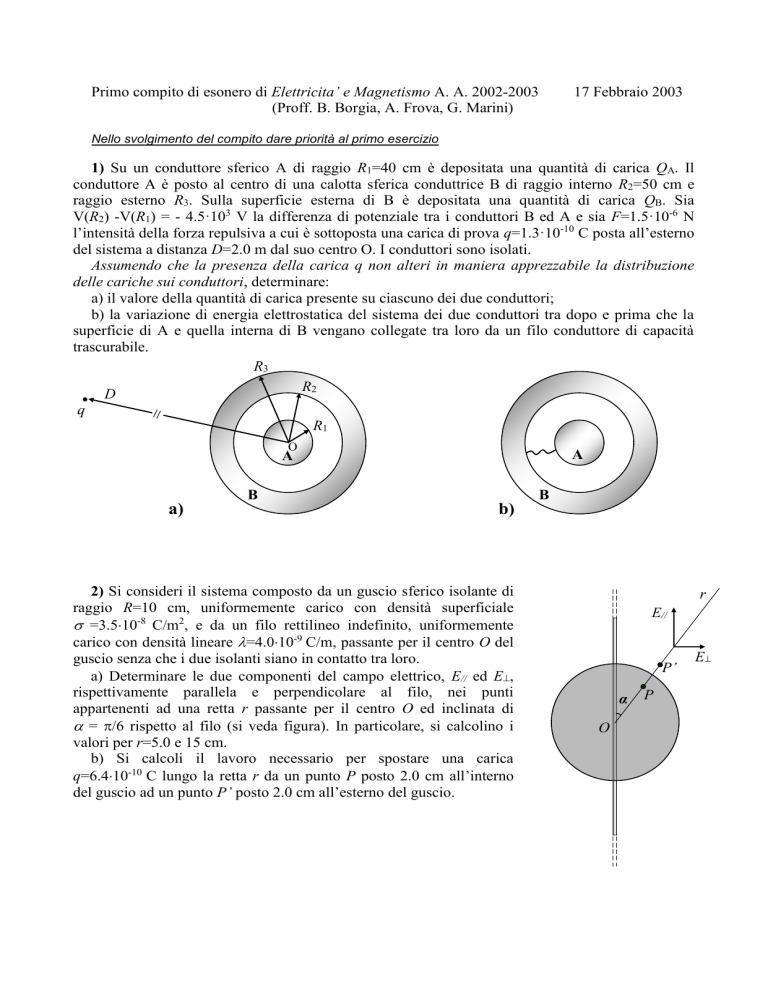
1) Su un conduttore sferico A di raggio R1=40 cm è depositata una quantità di carica QA. Il
conduttore A è posto al centro di una calotta sferica conduttrice B di raggio interno R2=50 cm e
raggio esterno R3. Sulla superficie esterna di B è depositata una quantità di carica QB. Sia
V(R2) -V(R1) = - 4.5·103 V la differenza di potenziale tra i conduttori B ed A e sia F=1.5·10-6 N
l’intensità della forza repulsiva a cui è sottoposta una carica di prova q=1.3·10-10 C posta all’esterno
del sistema a distanza D=2.0 m dal suo centro O. I conduttori sono isolati.
Assumendo che la presenza della carica q non alteri in maniera apprezzabile la distribuzione
delle cariche sui conduttori, determinare:
a) il valore della quantità di carica presente su ciascuno dei due conduttori;
b) la variazione di energia elettrostatica del sistema dei due conduttori tra dopo e prima che la
superficie di A e quella interna di B vengano collegate tra loro da un filo conduttore di capacità
trascurabile.
R3
R2
D
q
R1
O
A
A
B
a)
B
b)
2) Si consideri il sistema composto da un guscio sferico isolante di
raggio R=10 cm, uniformemente carico con densità superficiale
 =3.510-8 C/m2, e da un filo rettilineo indefinito, uniformemente
carico con densità lineare =4.010-9 C/m, passante per il centro O del
guscio senza che i due isolanti siano in contatto tra loro.
a) Determinare le due componenti del campo elettrico, E// ed E,
rispettivamente parallela e perpendicolare al filo, nei punti
appartenenti ad una retta r passante per il centro O ed inclinata di
 = /6 rispetto al filo (si veda figura). In particolare, si calcolino i
valori per r=5.0 e 15 cm.
b) Si calcoli il lavoro necessario per spostare una carica
q=6.410-10 C lungo la retta r da un punto P posto 2.0 cm all’interno
del guscio ad un punto P’ posto 2.0 cm all’esterno del guscio.
r
E//
P’
α
O
P
E
Soluzione Esercizio 1
Siano QA e QB le cariche distribuite sul conduttore A e B
rispettivamente. Tenendo conto dell’induzione elettrostatica tra i due
conduttori si realizza una situazione come quella in figura.
QA
- QA
(a) La differenza di potenziale tra i conduttori B e A è data da:
Q  R  R2 
 , da cui QA=1.0·10-6 C.
V ( R2 )  V ( R1 )  A  1
40  R1 R2 
QB + QA
La forza repulsiva sperimentata dalla carica di prova q è data da F  q
QA  QB
, da cui, nota QA,
40 D 2
QB=4.1·10-6 C.
(b) L’energia elettrostatica del sistema può essere calcolata da U 

1
 0 E 2 d
2
tutto
lo spazio
Prima del collegamento si ha
E

E


E

E

0

QA
40 r 2
0

r  R1
R1  r  R2
R2  r  R3
QA  QB
40 r 2
da cui U i 
1 QA2
2 40
 R2  R1  1 (QA  QB ) 2

 
 R2 R1  2 40 R3
r  R3
Dopo il collegamento si ha
E  0

QA  QB

E  4 r 2
0

r  R3
r  R3
1 QA2
Infine, Uf-Ui= 
2 40
da cui U f 
1 QA  QB 
2 40 R3
 R2  R1 

 = - 2.310-3 J.
 R2 R1 
2
Soluzione Esercizio 2


Indicando con E ed E rispettivamente i campi elettrici generati dal guscio sferico e dal filo
sulla retta r, tramite il teorema di Gauss si ottiene:
rR
0



 2
E 
nˆ (con n̂ versore normale al filo)
E   R
ˆ
r
r

R
2

r
sin

0
 r 2
 0
Le due componenti del campo elettrico parallela (E//) ed ortogonale (E) al filo lungo la
direzione definita dalla retta r sono:


rR
rR
0
 2 r sin 

 2
0
E  
E//   R
cos

r

R

R 2

 r 2

sin  r  R
 0
 20 r sin  0 r 2
Numericamente:
E// (r=5 cm)=0
E (r=5 cm)=2.9·103 V/m
E// (r=15 cm)=1.5·103 V/m
E (r=15 cm)=1.8·103 V/m
Per il calcolo del lavoro posso considerare separatamente il contributo dei due campi:
 R  2  sin  
P
P
 2 R2

R
dr

ds 
L  qV P  V P   q E  dl  q E  E   dl  q 


2
 0
r
20
s

P
P
R
 R  2  sin  



 R 2  1
1 

R  2
8
 q
ln
 

  6.1  10 J

R
R

2
2

R

2

0
 0 


