ROSSO ALESSANDRO

VILLA MIRCO
ITI EDOARDO AGNELLI – TORINO
IV ELN
Laboratorio di Elettronica
VILLA MIRCO
ITI – ISEAT Edoardo Agnelli
classe IV ELN
data: 6 ottobre 2003
Laboratorio di ELETTRONICA: Filtri
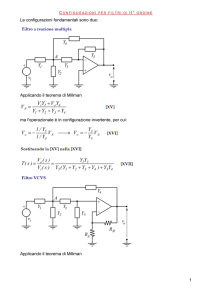
Parte I – Filtro passa basso

Obbiettivo del lavoro con filtro passa basso
Si realizzi un filtro passa basso che abbia come frequenza di taglio ft=2.50 kHz ed
una resistenza R del valore di 4,7 k.

Analisi dei dati ricevuti
Con i dati fornitici si calcola il valore che deve avere il condensatore dalla seguente
relazione: ft 

1
1
1
, si trova indi C come: C 
C
=15 nF
2RC
2Rft
6,28  4700  2500
Circuito sulla bread-board
Avendo il valore della resistenza [R] e del condensatore [C] calcolo il filtro e creo il
circuito sulla bread-board come mostrato sotto:
(fig 1.: R-C- sulla bread-board)
collegati allo stesso foro sulla scheda (v.fig.1) vi
sono resistenza e condensatore. Al terminale del condensatore
collego il puntale rosso mentre a quello della resistenza il nero, mandandoli all’oscilloscopio sul canale 1 (Cn 1) . All’altro reoforo della resistenza
collego il terminale rosso di un cavo BNC, mentre a quello nero è collegata l’altra
estremità del condensatore per recarsi “indi” al generatore di funzione (G.d.F.). Il
filtro che si va a realizzare è un filtro passa basso il cui funzionamento verrà
descritto in seguito.

Analisi del filtro passa basso
Il filtro realizzato è un filtro di tipo passa basso ossia che permette il passaggio di
tutte le frequenze al di sotto (cioè minori) di quella di taglio (f t=2.50 kHz) come
mostrato dallo schema seguente:
Pagina 1
VILLA MIRCO
IV ELN
ITI EDOARDO AGNELLI – TORINO
fig 2.:Filtro passa basso R-C
Laboratorio di Elettronica
fig. 3.: Grafico passa basso in V-f
Come mostra il grafico (fig. 3) l’uscita [Vu] coincide con l’entrata [Vi] solo se il
segnale d’ingresso ha frequenza compresa tra 0 e ft (0 <I < ft ); ovviamente per
frequenze maggiori di ft (f> ft) l’uscita è nulla.
Con frequenze pari a 0 (ft =0) il condensatore [C] si comporta come un circuito
aperto (poiché vale infinito) e l’uscita [Vu] è pari all’entrata [Vi] (se C  ∞Vu=Vi);
con frequenze che tende all’infinito (ft ∞) il condensatore si comporta come un
corto circuito, poiché:
Xc 
e come detto ft ∞ e quindi
1
ma  2f
jC
1
 0 il condensatore è un corto circuito.

Dal circuito di figura 2 si calcola mediante il partitore di tensione il valore della
tensione d’uscita Vu:
Vu  Vi 
Xc
:
R  Xc
essendo che si deve avere un’uguaglianza di unità di misura Volt=Volt non si può
inserire nel partitore il singolo valore del condensatore in quanto avrei:
Volt  Volt 
Farad
hm  Farad
bensì inserendo la capacità (misurata in Ohm) soddisfo tale uguaglianza.
Sostituendo il valore di Xc ottengo:
1
jC
Vu  Vi 
1
R
jC
facendo il minimo comun denominatore (mcm) la precedente relazione risulta
essere:
Pagina 2
VILLA MIRCO
ITI EDOARDO AGNELLI – TORINO
IV ELN
Vu  Vi 
Laboratorio di Elettronica
1
1  jC
La funzione di trasferimento (fdt) del circuito è il rapporto tra ingresso ed uscita
fdt 
OUT
IN
e nel caso del filtro passa basso essa risulta essere:
fdt 
OUT Vu
1


IN
Vi 1  jRC
Si definisce attenuazione il rapporto tra Vu e Vi: il rapporto tra la tensione d’uscita
e quella d’entrata:
A
Vu
.
Vi
L’attenuazione A nel filtro risulta essere come detto prima, uguale alla fdt:
A
1
1  jRC
razionalizzando il denominatore e compiendo gli opportuni calcoli si ottiene:
A
1  jRC
1
RC

j
2
1  jRC 1  jRC 1  (RC)
1  (RC) 2
1

che è quindi pari a:
1
(RC) 2
1  (RC) 2
A


1  (RC) 2 1  (RC) 2
[1  (RC) 2 ]2
semplificando ottengo l’attenuazione A pari ad:
A
1
1(RC)
2
sapendo che w=1/RC ed andando a sostituire si nota che:
A
1

1
1 (
RC)
RC
1
11

1
2
 0,7
osservando, la tabella delle misurazioni si noti che in corrispondenza della
frequenza di taglio l’attenuazione vale ca. 0,7.
In corrispondenza di f=0: l’attenuazione A risulta essere A/1 quindi A, in
corrispondenza di f= ∞ A varrebbe 1/∞ e quindi 0, ed il comportamento
in
corrispondenza della frequenza di taglio è stato descritto sopra.
Pagina 3
VILLA MIRCO
ITI EDOARDO AGNELLI – TORINO
IV ELN
Laboratorio di Elettronica
Si definisce t sfasamento teorico :
 t  arctg
f
ft
successivamente si va anche a calcolare lo sfasamento pratico del quale verrà
illustrato in seguito.

Misurazioni:
Premesse queste cose (vedi punto precedente) si passa alla misurazione riportando
i dati riscontrati nella tabella:
 legenda tabella:

1 colonna: f [Hz] impostata sul Gdf

2 colonna: Vi [V]  la tensione d’entrata

N.B.: sul Gdf è stato impostato 1V, ma si tratta di tensione
picco-picco data dalla relazione Vi=2Vpp; per cui sulla tabella
compaiono 2V

3 colonna: Vu [V] il valore di tensione d’uscita letto sull’oscilloscopio
A  è dimensionale [V/V] è data da come detto in
 4 colonna:
precedenza dal rapporto tra la tensione d’uscita e quella
d’entrata
 5 colonna: A [dB] l’attenuazione (v IV col) in Decibel data dalla
relazione Adb= 20logA

f(Hz)
Vi(V)
6 colonna: t lo sfasamento teorico
Vu(V)
A
A(db)
t
alla tabella affianco come mostrato sotto
è
300
2
2
1
0
-6.84
500
2
2
1
0
-11.30
rappresentante lo sfasamento pratico,
700
2
2
1
0
-15.64
calcolato
mediante
1000
2
1.9
0.95
-0.44
-21.80
prendendo
l’uscita
1100
2
1.9
0.95
-0.44
-23.74
collegandola mediante cavo BNC allo
1150
2
1.8
0.9
-0.91
-27.70
strumento, posizionando dapprima le
1315
2
1.8
0.9
-0.91
-24.70
manopole su GND (sullo schermo si
2500
2
1.2
0.6
-4.43
-45
visualizza un puntino) e spostando le
3000
2
1.1
0.55
-5.19
-50.19
levette di Cn 1 e Cn 2 si ottengono indi
4000
2
1
0.5
-6.02
-57.99
due segmenti di ugual lunghezza.
5000
2
0.8
0.4
-7.95
-63.43
Muovendo nuovamente le manopole su
stata
aggiunta
una
colonna
l’oscilloscopio:
dal
circuito
e
AC si visualizza un ellisse e dalla
formula:
Pagina 4
VILLA MIRCO
ITI EDOARDO AGNELLI – TORINO
IV ELN
5500
2
0.76
0.38
-8.40
-65.55
10000
2
0.42
0.21
-13.55
-75.96
20000
2
0.22
0.11
-19.17
-82.87
50000
2
0.1
0.05
-26.02
-87.13
Laboratorio di Elettronica
b
: si calcola lo
a
sfasamento teorico
 p  arcsen
Tab 1.:tabella misurazioni tensione d’uscita, d’ingresso attenuazione
b
Fig. 4 immagine che viene visualizzata
sull’oscilloscopio ed indicazione di b ed a
a
Viene riportata di seguito la tabella con i dati riguardanti lo sfasamento pratico:
b
a
b/a
p
300
0.8
6.0
0.13
-8.51
-6.84
500
1.2
6.0
0.2
-12.80
-11.30
700
1.7
6.1
0.27
-17.97
-15.64
1000
2.4
6.1
0.39
-25.74
-21.80
1100
2.5
6.1
0.40
-26.88
-23.74
1150
2.7
6.1
0.44
-29.19
-27.70
1315
2.9
5.9
0.49
-32.71
-24.70
2500
1.2
5.9
0.71
-50.42
-45
3000
4.5
5.6
0.96
-59.41
-50.19
4000
5
5.8
0.80
-66.16
-57.99
5000
5.1
5.8
0.86
-75.57
-63.43
5500
5.2
5.7
0.91
-73.13
-65.55
10000
5.4
5.6
0.96
-82.93
-75.96
20000
5.8
6.0
0.96
-83.51
-82.87
50000
5.8
5.8
1.00
-90
-87.13
f (Hz)
t
Tab 2.:tabella misurazoni sfasamento pratico e teorico
Pagina 5
VILLA MIRCO

ITI EDOARDO AGNELLI – TORINO
IV ELN
Laboratorio di Elettronica
Conclusioni:
Da come si evince dalla Tab.1 la tensione d’uscita si discosta poco da 2 V fino alla
frequenza di 2500 Hz (2.5 kHz – frequenza di taglio), poiché il filtro è un “passa
basso” e come tale permette il passaggio delle frequenze minori di quelle di taglio.
Dalla Tab.2 si evince che gli sfasamenti teorico e pratico (t, p) discostano poco
come valore.
Parte II – Filtro passa alto

Obbiettivo del lavoro con filtro passa alto
Si realizzi un filtro passa alto che abbia come frequenza di taglio ft=2.50 kHz ed una
resistenza R del valore di 4,7 k.

Analisi dei dati ricevuti
I dati fornitici sono identici per le misurazioni del filtro passa basso:


Resistenza: 4.7 k.

Condensatore: 15 nF

Frequenza di taglio: 2.50 kHz
Circuito sulla bread-board
Avendo il valore della resistenza [R] e del condensatore [C] calcolo il filtro e creo il
circuito sulla bread-board come mostrato sotto:
(fig 4.:C-R- sulla bread-board)
collegati allo stesso foro sulla scheda (v.fig.1) vi
sono resistenza e condensatore. Al terminale della resistenza collego
il puntale rosso mentre a quello del condensatore il nero, mandandoli all’oscilloscopio sul canale 1 (Cn 1) . All’altro reoforo del condensatore
collego il terminale rosso di un cavo BNC, mentre a quello nero è collegata l’altra
estremità della resistenza per recarsi “indi” al generatore di funzione (G.d.F.). Il filtro
che si va a realizzare è un filtro passa alto il cui funzionamento verrà descritto in
seguito.

Analisi del filtro passa basso
Il filtro realizzato è un filtro di tipo passa alto ossia che permette il passaggio di
tutte le frequenze al di sopra (cioè maggiori) di quella di taglio (ft=2.50 kHz) come
mostrato dallo schema seguente:
Pagina 6
VILLA MIRCO
ITI EDOARDO AGNELLI – TORINO
IV ELN
fig 5.:Filtro passa alto C-R
Laboratorio di Elettronica
fig. 6.: Grafico passa alto in V-f
Come mostra il grafico (fig. 6) l’uscita [Vu] coincide con l’entrata [Vi] solo se il
segnale d’ingresso ha frequenza maggiore di quella di taglio (I>f t) ovviamente per
frequenze minori di ft (f< ft) l’uscita è nulla.
Con frequenze pari a 0 il condensatore si comporta come un circuito aperto e con
frequenza che tende all’infinito come un corto circuito
La tensione di uscita Vu è pari a:
Vu 
Vi  R
1
R j
C
dividendo ambedue denominatore e numeratore per R si ottiene:
Vu
A
Vi
1
1 j
1
RC
ossia l’attenuazione A. Viene definita frequenza di taglio quella frequenza a cui
corrisponda un’attenuazione
A
1
2

 A  0,7
e uno sfasamento =45°: quindi RC=1 per cui
t 
1
RC
t viene detta pulsazione di taglio.
Mentre la frequenza di taglio ft 

1
.
2RC
Misurazioni:
Premesse queste cose (vedi punto precedente) si passa alla misurazione
riportando i dati riscontrati nella tabella (la cui legenda per la lettura è riportata nella
parte I – Filtro passa basso – Misurazioni)
Pagina 7
VILLA MIRCO
f(Hz)
ITI EDOARDO AGNELLI – TORINO
IV ELN
Vi(V)
Vu(V)
A
A(db)
t
b
Laboratorio di Elettronica
a
b/a
p
300
2
0.28
0.14 -17.007
6.84
5.6
6
0.93
68.96
500
2
0.44
0.22 -13.151
11.3
5.7
5.9
0.96
73.77
700
2
0.6
0.3 -10.457
15.64
5.9
6
0.98
78.52
1000
2
0.8
0.4
-7.958
21.8
5.6
6.2
0.90
64.15
1100
2
0.88
0.44
-6.937
23.74
5.6
5.7
0.98
75.52
1150
2
0.9
0.45
-6.935
24.70
5.3
5.5
0.94
70.00
1315
2
1
0.5
-6.020
27.74
5.2
5.5
0.94
70.00
2500
2
1.48
0.74 -2.6157
45
3.1
5.6
0.55
33.36
3000
2
1.5
0.75 -2.4987
50.19
3.5
5.7
0.61
37.58
4000
2
1.6
0.8 -1.9382
57.99
2.9
5.7
0.50
30
5000
2
1.8
0.9
-0.915
63.43
2.7
6
0.45
26.74
5500
2
1.84
0.92
-0.724
65.55
2.2
5.6
0.39
23.00
10000
2
1.9
0.95 -0.4455
75.96
1.2
5.6
0.21
12.12
20000
2
1.94
0.97 -0.2645
82.87
0.7
5.9
0.11
6.31
50000
2
2
87.13
0.4
0.6
0.66
41.81
1
0
Pagina 8