1) Un corpo di massa m1= 1 kg di muove su un piano orizzontale

CORSO DI LAUREA IN SCIENZE BIOLOGICHE
Prova scritta di FISICA – 18 Luglio 2007
1) Un corpo di massa m1= 500 gr si muove su un piano orizzontale scabro, con coefficiente di attrito dinamico
 = 0.4, partendo con velocità v0 = 10 m/s. Dopo avere percorso un tratto d, al termine del quale ha velocità
v1= 5 m/s, urta in modo completamente anelastico un corpo di massa m2 = 100 g.
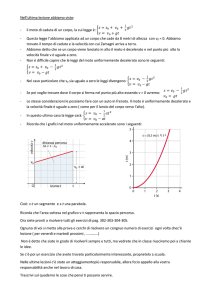
Dopo l'urto i due corpi proseguono il loro moto lungo un
pendio liscio, inclinato di 30° rispetto all’orizzontale, come
 mostrato in figura. Determinare:
h
a) la lunghezza del tratto d;
b) la velocità dei corpi immediatamente dopo l'urto e la
massima quota h raggiunta sul pendio.
m1
m2
300
2) Una carica positiva Q = 5 10 -15 C è fissata ad un punto O . Una particella di massa m= 10 -20 g e carica negativa
q = -2 10 -17 C si muove uniformemente su una traiettoria circolare di centro O e raggio R = 10 -6 m.
Determinare:
a) il modulo della velocità della carica q;
b) l’energia totale del sistema delle due cariche.
(N.B. 0 = 8.85 10-12 C2/Nm2 )
3) Una cisterna cilindrica, di raggio R1 = 1 m e di altezza L, è posta a quota h rispetto
al suolo ed è piena d’acqua. La cisterna è aperta superiormente e sulla base inferiore
presenta un forellino di raggio R2 = 1cm dal quale l’acqua fuorisce con
velocità v2 = 5 m/s, come mostrato in figura. Determinare:
y
v1
L
v2
a) la velocità dell’acqua in corrispondenza alla base superiore della cisterna;
b) l’altezza L della cisterna, facendo le opportune approssimazioni;
c) facoltativo: l’altezza h a cui è posta la cisterna,
sapendo che il tempo di caduta dell’acqua dal forellino al suolo è pari a t = 1 s.
h
0
x
4) Due moli di gas perfetto biatomico compiono una trasformazione dallo stato A a pressione pA = 2 atm e volume
VA = 1 l allo stato B a pressione 2pA e volume VB. Durante la trasformazione la pressione varia linearmente con
il volume ed il gas compie un lavoro pari a WAB = +100 J. Determinare:
a) le coordinate termodinamiche (p,V,T) degli stati A e B, dopo avere disegnato il grafico della trasformazione nel
piano p-V;
b) il calore QAB scambiato nella trasformazione, specificandone il segno.
SCRIVERE IN MODO CHIARO. GIUSTIFICARE BREVEMENTE I PROCEDIMENTI.
SOSTITUIRE I VALORI NUMERICI SOLO ALLA FINE. NON SCORDARE LE UNITA` DI MISURA.
Testi, soluzioni ed esiti alle pagine: www2.fisica.unimi.it/bettega/ (AD), fisbio.webhop.net (EN),
www.mi.infn.it/~sleoni (OZ)
SOLUZIONE ESERCIZIO 1
a) Durante il moto lungo il tratto orizzontale d l’unica forza che compie lavoro è la forza di attrito.
Dal teorema lavoro-energia cinetica si ottiene quindi:
K  Latt
 
1
1
m1v12  m1v02  f d  d    m1 gd
2
2
2
v0  v12
(10 2  52 )m 2 / s 2
d

 9.6 m
2 g
2  0.4  9.8m / s 2
b) Dopo l’urto i due corpi proseguono uniti. Per la conservazione della quantità di moto:
m1v1  0  ( m1  m2 )v
v
m1
v1
m1  m2
0.5kg
5m / s
0.5kg  0.1kg
 4.2 m / s

La massima quota h raggiunta lungo il piano inclinato si può determinare applicando il principio di
conservazione dell’energia meccanica, dato che in questo caso esistono solo forze conservative.
E mecc ,1  E mecc , 2
1
( m1  m2 )v 2  ( m1  m2 ) gh
2
4.2 m / s 2  0.9 m
v2
h

2 g 2  9.8m / s 2
SOLUZIONE ESERCIZIO 2
a) La forza centripeta che determina il moto circolare uniforme della carica q è la forza di attrazione
elettrostatica esercitata da Q su q . E’ pertanto :
(kQq)/R2 =m v2 /R
(1)
dove k = 1/ 4πεo e Q e q sono i valori assoluti delle cariche
Si ricava v e sostituendo i valori numerici si ottiene :
v = 9.5 10 3 m/s
b) L’energia E del sistema delle due cariche è la somma dell’energia cinetica e dell’energia potenziale di q
nel campo elettrostatico di Q.
E = ½ mv2 - (k Q q) / R
(2)
dove Q e q sono i valori assoluti delle cariche.
Sostituendo i valori numerici si ottiene E = - 4.5 10 -16 J
Notare che dalla (1) risulta ½ mv2 = ½ (k Q q) / R e pertanto E = - ½ ( k Q q ) / R = E = - 4.5 10 -16 J
SOLUZIONE ESERCIZIO 3
a) La velocità v1 dell’acqua in corrispondenza della superficie superiore A1 della cisterna si ricava
dall’equazione di continuità:
A1v1  A2 v2
R12 v1  R22 v2
102 m  5m / s  5  104 m / s
R2
v1  22 v2 
R1
1m 2
2
b) In base al teorema di Bernoulli:
1
1
p0  v12  g ( L  h)  p0  v22  gh
2
2
1 2
1
v1  gL  v22
2
2
2
2
1  (v2  v1 ) 1 v22
(5m / s ) 2
L


 1.28m
2
g
2 g 2  9.8m / s 2
c) facoltativo:
le gocce d’acqua che fuoriescono dal forellino cadono al suolo con moto rettilineo e uniformemente
accelerato, essendo soggette all’accelerazione di gravità g. In base alle leggi del moto uniformemente
accelerato lungo l’asse verticale y si ottiene:
1
y  y0  v0 y t  gt 2
2
1
0  h  v0 y t  gt 2
2
1
h  v0 y t  gt 2
2
1
 (5m / s )  (1s )   (9.8m / s 2 )  (1s ) 2
2
 9.9m
SOLUZIONE ESERCIZIO 4
a) Il lavoro compiuto dal gas durante la trasformazione lineare da A a B è pari all’area del trapezio ABVAVB,
rappresentato in figura. Le coordinate termodinamiche (p,V,T) valgono quindi:
Stato A:
p
pA = 2 atm = 2 x 105 Pa
VA = 1 l = 10-3 m3
TA = pAVA/(nR)
= (2 x 105 Pa  10-3 m3)/(2  8.31J/moleK)
= 12 K
B
pB=2pA
pA
A
Stato B:
pB = 2pA = 4 atm = 4 x 105 Pa
per ricavare il volume VB utilizzo l’espressione del lavoro
WAB svolto dal gas:
( p A  p B )  (VB  V A )
2
2  W AB
(VB  V A ) 
( p A  pB )
W AB 
VB  V A 
2  W AB
( p A  pB )
 10 3 m 3 
2  10 2 Nm
( 2  4)  105 N / m 2
 (1  1 / 3)10 3 m 3  4 / 3  10 3 m 3
 1.33  10 3 m 3  1.33 l
TB = pBVB/(nR)
= (4 x 105 Pa  1.33 10-3 m3)/(2  8.31J/moleK)
= 32 K
b) In base al primo principio della termodinamica:
Q  Eint  W
5
 nR(TB  TA )  W AB
2
5
  2moli  8.31J /( moleK )(32  12) K  100 J
2
  931 J
0
VA
VB
V