LICEO SCIENTIFICO “CAVOUR”
TEST DI FISICA PER LA CLASSE 3D
Durata della prova 1 ora e 30 minuti
COMPITO A
Quesito n.1
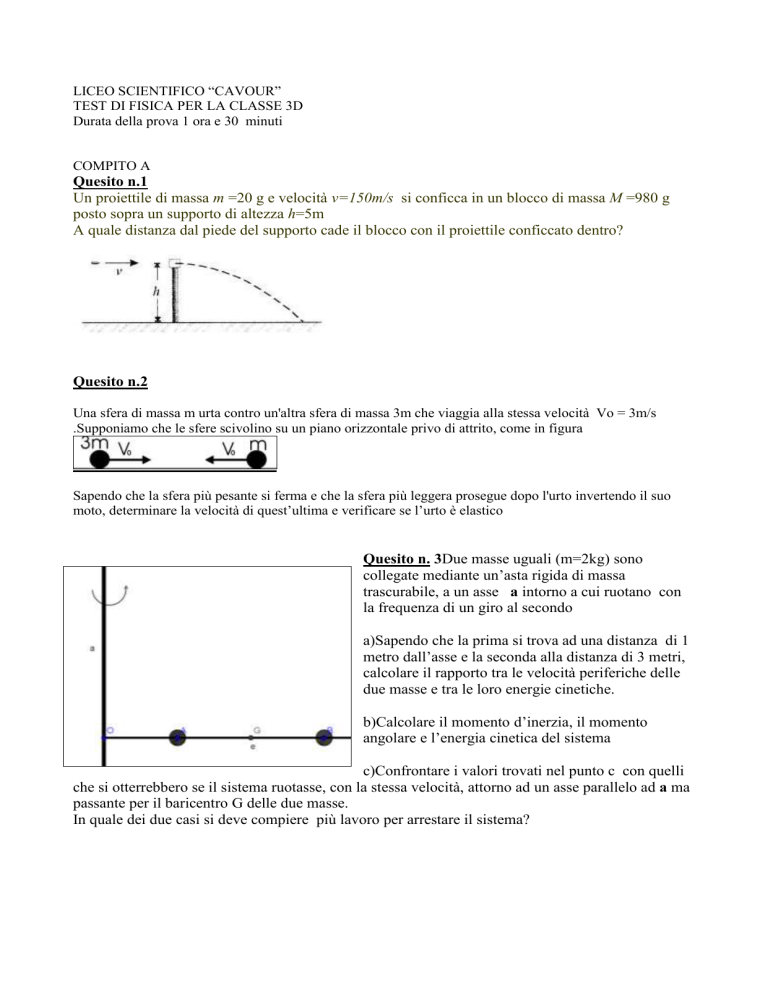
Un proiettile di massa m =20 g e velocità v=150m/s si conficca in un blocco di massa M =980 g
posto sopra un supporto di altezza h=5m
A quale distanza dal piede del supporto cade il blocco con il proiettile conficcato dentro?
Quesito n.2
Una sfera di massa m urta contro un'altra sfera di massa 3m che viaggia alla stessa velocità Vo = 3m/s
.Supponiamo che le sfere scivolino su un piano orizzontale privo di attrito, come in figura
Sapendo che la sfera più pesante si ferma e che la sfera più leggera prosegue dopo l'urto invertendo il suo
moto, determinare la velocità di quest’ultima e verificare se l’urto è elastico
Quesito n. 3Due masse uguali (m=2kg) sono
collegate mediante un’asta rigida di massa
trascurabile, a un asse a intorno a cui ruotano con
la frequenza di un giro al secondo
a)Sapendo che la prima si trova ad una distanza di 1
metro dall’asse e la seconda alla distanza di 3 metri,
calcolare il rapporto tra le velocità periferiche delle
due masse e tra le loro energie cinetiche.
b)Calcolare il momento d’inerzia, il momento
angolare e l’energia cinetica del sistema
c)Confrontare i valori trovati nel punto c con quelli
che si otterrebbero se il sistema ruotasse, con la stessa velocità, attorno ad un asse parallelo ad a ma
passante per il baricentro G delle due masse.
In quale dei due casi si deve compiere più lavoro per arrestare il sistema?
COMPITO B
Quesito n.1
Un carrellino pieno di sabbia avente massa complessiva di 20 kg si
muove verso sinistra, lungo un piano orizzontale senza attrito alla
velocità di 0,5 m s-1. Una palla di massa 1 kg, mentre si muove
orizzontalmente verso destra a 14 m s-1, colpisce il carrellino e
resta conficcata nella sabbia.
Determinare il modulo e il verso della velocità del sistema dopo l'urto.
Quesito n2 Un oggetto di massa 6 Kg viene lanciato verticalmente verso l'alto.
Nell'istante in cui si trova fermo, ad una altezza di 5 m dal suolo, esplode e si spezza in due
frammenti,di massa una doppia dell'altra, che cadono verso il suolo . .
Gli attriti sono trascurabili.
a) Dopo quanto tempo giungeranno al suolo i due frammenti?
Questo tempo e` diverso da quello che avrebbe impiegato l'oggetto a ricadere al suolo, se non fosse
esploso?
b) Se il frammento minore cade ad una distanza orizzontale di 10 m, dal punto dell'esplosione, a
quale distanza dallo stesso punto si trova il maggiore?
Con quale velocità si muoveva ciascun frammento subito dopo l'esplosione? Come si muoveva il
baricentro del sistema?
c)Quanta energia si e` sviluppata nell'esplosione?
Quesito n.3 Un manubrio è costituito da due masse uguali collegate da una sbarretta di massa
trascurabile di lunghezza
: supponiamo che inizialmente esso ruoti liberamente intorno ad un
asse ortogonale al centro della sbarretta con velocità angolare . Se in virtù di forze interne le due
masse vengono avvicinate in maniera da distare alla fine solo
dal centro dell'asse di rotazione.
Determinare: La velocità angolare finale del sistema ed il lavoro fatto dalle forze interne.
(dati del problema
,
,
)
SOLUZIONI
Compito A
Quesito n.1
L'urto tra il proiettile e il blocco è anelastico; per la conservazione della quantità di moto, i due si
muovono insieme dopo l'urto, con velocità
Dall'analisi della componente verticale del moto (uniformemente accelerato) si ricava che il tempo
di caduta è
La componente orizzontale del moto è invece uniforme; pertanto il blocco cade ad una distanza dal
piede del supporto data da
.
Sostituendo i valori assegnati si trova d=3m.
Quesito n.2
Poiché sul sistema non agiscono forze esterne la quantità di moto complessiva si conserva, pertanto
possiamo scrivere
3mv0-mv0=0+mv1
(avendo scelto come verso positivo del moto quello della massa maggiore)
da cui v1=2v0= 6m/s
Per verificare se l’urto è elastico si deve confrontare l’energia cinetica iniziale con quella finale
Energia iniziale
Energia finale
L’urto è elastico
Quesito n. 3
Le due masse si muovono con la stessa velocità angolare, =2πf = 2π rad/s , quindi le velocità
periferiche sono direttamente proporzionali alle distanze dall’asse di rotazione
Il rapporto delle due energie cinetiche è invece uguale al quadrato del rapporto delle velocità, quindi
=
=40*π2J
Se il sistema ruota intorno ad un asse passante per il baricentro
momento di inerzia
Momento angolare
L’=I’*=8π J*s
energia cinetica
J
Per arrestare il sistema deve compiere maggior lavoro nel primo caso , in cui l’energia cinetica è
maggiore
Compito B
Quesito n.1
Si tratta di un urto completamente anelastico per il quale è valido il principio di conservazione della
quantità di moto poiché non agiscono, sul sistema, forze esterne non equilibrate.
Considerando positivo il verso di moto della palla, si trova
Dopo l'urto il sistema si muove verso destra, cioè nel verso del moto iniziale della palla
Quesito n2
a)I due frammenti avranno massa 4Kg e 2Kg, rispettivamente.
Il tempo di caduta non dipende dalla massa dell’oggetto, quindi i due frammenti giungeranno al
suolo dopo un tempo
, pari a 1 s circa.
Questo è anche il tempo che avrebbe impiegato l'oggetto a ricadere al suolo, se non fosse
esploso.
b) Durante l’esplosione non cambia la componente orizzontale della quantità di moto, quindi
possiamo scrivere
2mv1-mv2=0(avendo scelto come verso positivo del moto quello della massa maggiore)
da cui 2mv1 = mv2→ le due velocità sono inversamente proporzionali alle masse, ovvero
Poiché le gittate dei due proiettili sono direttamente proporzionali alle componenti orizzontali delle
velocità, possiamo affermare che il frammento maggiore cadrà ad una distanza di 5m dal punto
dell'esplosione
Tenendo conto del tempo di caduta possiamo calcolare i valori delle due velocità
v1 = 5m/s e v2= 10 m/s
Il baricentro del sistema si muove come se l’esplosione non fosse avvenuta, quindi cade
liberamente lungo la verticale
c) L’energia sviluppata nell’esplosione è uguale alla somma delle energie cinetiche dei due
frammenti
= 150 J
Quesito n3
Quando le masse si avvicinano cambia il momento di inerzia del sistema e poiché il sistema è
isolato si conserva il momento angolare.
Possiamo pertanto scrivere
Poiché il momento di inerzia iniziale è
mentre quello finale è
ovvero ¼ di quello iniziale, sarà f = 4i = 80 rad/s
Il lavoro compiuto dalle forze interne corrisponde alla differenza tra l’energia cinetica iniziale e
quella finale.
=
Sostituendo i valori numerici si ottiene (800-200=600) J












