Omotetia

Costruzione
OMOTETIA
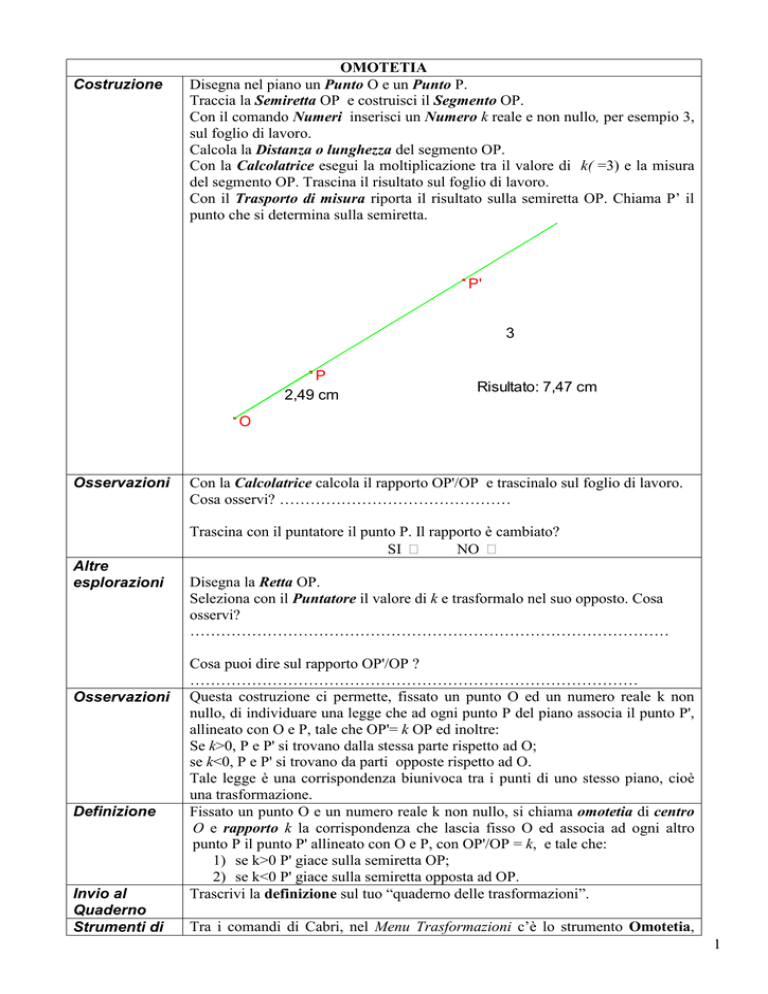
Disegna nel piano un Punto O e un Punto P.
Traccia la Semiretta OP e costruisci il Segmento OP.
Con il comando Numeri inserisci un Numero k reale e non nullo, per esempio 3,
sul foglio di lavoro.
Calcola la Distanza o lunghezza del segmento OP.
Con la Calcolatrice esegui la moltiplicazione tra il valore di k( =3) e la misura
del segmento OP. Trascina il risultato sul foglio di lavoro.
Con il Trasporto di misura riporta il risultato sulla semiretta OP. Chiama P’ il
punto che si determina sulla semiretta.
P'
3
P
2,49 cm
Risultato: 7,47 cm
O
Osservazioni
Con la Calcolatrice calcola il rapporto OP'/OP e trascinalo sul foglio di lavoro.
Cosa osservi? ………………………………………
Trascina con il puntatore il punto P. Il rapporto è cambiato?
SI 
NO 
Altre
esplorazioni
Osservazioni
Definizione
Invio al
Quaderno
Strumenti di
Disegna la Retta OP.
Seleziona con il Puntatore il valore di k e trasformalo nel suo opposto. Cosa
osservi?
…………………………………………………………………………………
Cosa puoi dire sul rapporto OP'/OP ?
……………………………………………………………………………
Questa costruzione ci permette, fissato un punto O ed un numero reale k non
nullo, di individuare una legge che ad ogni punto P del piano associa il punto P',
allineato con O e P, tale che OP'= k OP ed inoltre:
Se k>0, P e P' si trovano dalla stessa parte rispetto ad O;
se k<0, P e P' si trovano da parti opposte rispetto ad O.
Tale legge è una corrispondenza biunivoca tra i punti di uno stesso piano, cioè
una trasformazione.
Fissato un punto O e un numero reale k non nullo, si chiama omotetia di centro
O e rapporto k la corrispondenza che lascia fisso O ed associa ad ogni altro
punto P il punto P' allineato con O e P, con OP'/OP = k, e tale che:
1) se k>0 P' giace sulla semiretta OP;
2) se k<0 P' giace sulla semiretta opposta ad OP.
Trascrivi la definizione sul tuo “quaderno delle trasformazioni”.
Tra i comandi di Cabri, nel Menu Trasformazioni c’è lo strumento Omotetia,
1
Cabri
che consente di disegnare un punto P' omotetico di P rispetto un punto fissato O
secondo il rapporto di omotetia k, indicando il punto. Il centro ed il numero che
indica il rapporto di omotetia.
2
Costruzione
SEGMENTI NELL’OMOTETIA
Costruisci un Punto O, due Punti P e Q distinti da O e il Segmento PQ.
Inserisci nel foglio di lavoro un Numero reale k non nullo, per es. 3.
Siano P' e Q' i corrispondenti di P e Q nella Omotetia di centro O e rapporto
k.
Traccia il Segmento P'Q'.
Costruisci R un punto appartenente al segmento PQ ed il suo corrispondente
R' nella Omotetia di centro O e rapporto k.
P'
R'
Q'
3
P
R Q
O
Indagine
Con lo strumento appartiene a? verifica se R' appartiene a P'Q'.
 SI
 NO
Controllo
Trascina R con il puntatore . La tua osservazione è ancora vera?
 SI
 NO
In un’ omotetia a segmenti corrispondono …………………….
Congettura
Invio al
quaderno
Osservazioni
Altre
esplorazioni
Questa congettura è vera. Trascrivila sul tuo “quaderno delle trasformazioni”
come Proprietà 1..
Con il comando Distanza o Lunghezza calcola la misura del segmento PQ e
del segmento P'Q'.
Con la Calcolatrice calcola il rapporto P'Q'/PQ. Cosa osservi?
…………………………………………………………………………
Trascina con il puntatore il punto P o Q, il rapporto è cambiato?
SI

NO

Con il comando Parallelo? verifica se i segmenti PQ e P'Q' sono paralleli.
SI 
NO 
Fai variare P o Q. La tua risposta è sempre la stessa?
SI 
NO 
Congettura
Invio al
Quaderno
Due segmenti PQ e P'Q' che si corrispondono in una omotetia di centro O e
rapporto k sono …………. e tali che P'Q'/PQ = …….
Tale congettura è vera. Trascrivila come proprietà 2 sul tuo “quaderno delle
trasformazioni”.
3
RETTE NELL’OMOTETIA
Costruzione
Costruisci un Punto O e inserisci nel foglio di lavoro un numero k, per es. 3.
Costruisci una Retta r.
3
Con lo strumento punto su un oggetto disegna due punti P e Q su r. Siano P' e Q'
rispettivamente i corrispondenti di P e Q nell’omotetia di centro O e rapporto k. Traccia la
retta P'Q' e chiamala r'.
Con punto su un oggetto disegna un punto R su r e costruisci il suo corrispondente R'
nell’omotetia di centro O e rapporto k.
R'
3
R
Q'
Q
O
P
P'
r
r'
Indagine
Controllo
Congettura
Invio al
quaderno
Indagine
Controllo
Congettura
Invio al
quaderno
Con lo strumento appartiene a? verifica se R' appartiene ad r'.
 SI
 NO
Trascina R con il puntatore . La tua osservazione è ancora vera?
 SI
 NO
In una omotetia a rette corrispondono ……….
La precedente congettura è vera. Trascrivila come proprietà 3 sul tuo “quaderno delle
trasformazioni”.
Con lo strumento parallelo? verifica se r ed r' sono parallele.
 SI
 NO
Trascina r e falla ruotare con il puntatore. La tua osservazione è ancora vera?
 SI
 NO
Se fai passare r per O cosa accade?..........
In una omotetia rette corrispondenti sono ……… e rette passanti per il centro sono ………
La precedente congettura è vera. Trascrivila come proprietà 4 sul tuo “quaderno delle
trasformazioni”.
4
Costruzione
TRIANGOLI NELL’OMOTETIA
Costruisci un punto O e inserisci nel foglio di lavoro un numero k non nullo, per
es. 3.
Costruisci tre punti non allineati P, Q ed R e il triangolo PQR.
Dal Menu trasformazioni seleziona Omotetia e costruisci, nell’omotetia di centro
O e rapporto k, i corrispondenti dei punti P, Q ed R e chiamali rispettivamente P',
Q', R'.
Disegna il triangolo P'Q'R'.
R'
P'
3
R
P
O
Q'
Q
Indagine
Disegna un Punto X nel piano e il suo corrispondente X' nella Omotetia di
centro O e rapporto k.
Trascina il punto X.
Se X si muove fuori dal triangolo PQR allora X' ….............................................
……………………………………………………………………………………
Se X si muove nel triangolo PQR allora X' …......................................................
……………………………………………………………………………………
Congettura
Invio al
quaderno
Osservazioni
In una Omotetia di centro O e rapporto k a triangoli corrispondono ……………
La precedente congettura è vera. Trascrivila come proprietà 5 sul tuo “quaderno
delle trasformazioni”.
Poiché segmenti corrispondenti in una omotetia sono paralleli, nei due triangoli
lati corrispondenti sono ……..
Calcola il rapporto tra il perimetro del triangolo P'Q'R' ed il perimetro del
triangolo PQR. Cosa noti?
Altre
esplorazioni
Con il comando Misura dell’angolo calcola le ampiezze degli angoli interni dei
due triangoli. Cosa osservi?
…………………………………………………………………………….
Angoli corrispondenti sono……..

Congettura
Invio al
Quaderno
Indagine
Due triangoli PQR e P'Q'R' che si corrispondono in una omotetia hanno i lati
corrispondenti ……………. e gli angoli corrispondenti …….. .
Tale congettura è vera. Trascrivila come proprietà 6 sul tuo “quaderno delle
trasformazioni”.
Calcola il perimetro di PQR e il perimetro di P'Q'R'.
Con la calcolatrice calcola il rapporto tra il perimetro del triangolo P'Q'R' ed il
perimetro del triangolo PQR. Cosa noti? ……………………
5
Calcola l’area di PQR e l’area di P'Q'R'.
Con la calcolatrice calcola il rapporto tra l’area del triangolo P'Q'R' e l’area del
triangolo PQR. Cosa noti? ……………………
Congettura
Invio al
quaderno
Siano PQR e P'Q'R' due triangoli che si corrispondono in una omotetia di
rapporto k. Si ha:
Il rapporto tra il perimetro di P'Q'R' e quello di PQR vale ………
Il rapporto tra l’area di P'Q'R' e quella di PQR vale ………
Tale congettura è vera. Trascrivila come Proprietà 7 sul tuo “quaderno delle
trasformazioni”.
6
Proprietà
PUNTI NOTEVOLI DEI TRIANGOLI NELLA OMOTETIA
E’ possibile dimostrare che
In due triangoli corrispondenti in una omotetia al baricentro dell’uno corrisponde il
baricentro dell’altro.
In due triangoli corrispondenti in una omotetia all’incentro dell’uno corrisponde
l’incentro dell’altro.
In due triangoli corrispondenti in una omotetia al circocentro dell’uno corrisponde
il circocentro dell’altro.
In due triangoli corrispondenti in una omotetia all’ ortocentro dell’uno corrisponde
l’ortocentro dell’altro.
Puoi verificare tale proprietà con gli strumenti di Cabri.
Invio al
quaderno
Trascrivi le proprietà sul tuo “quaderno delle trasformazioni”come Proprietà 8,
Proprietà 9, Proprietà 10, Proprietà 11.
7