CORSO DI CULTURA NAUTICA
Lezione 12
Cenni di geografia astronomica.- ( Parte III )
1. La misura del tempo – cenni storici
A partire dall’antichità, il movimento “apparente“ del Sole e degli astri
intorno alla Terra aveva costituito quasi l’unico (certamente il più
immediato ed istintivo) strumento a disposizione dell’uomo a cui riferirsi
per misurare lo scorrere del tempo.
Ancora fino a qualche decennio fa l’astronomia e la scienza della
navigazione avevano progressivamente messo a punto tecniche sempre più
precise su cui contare per misurare lo scorrere del tempo, riferendosi al
movimento degli astri nel cielo.
La velocità di rotazione della Terra intorno al suo asse è assolutamente
costante e quindi la durata tra due passaggi di un determinato astro, per
esempio al meridiano superiore, può essere utilizzato come riferimento per
la durata dell’arco diurno.
(Nota: in realtà la velocità di rotazione della Terra non è costante in
assoluto, ma tende a ridursi progressivamente - anche se in misura
impercettibile - per effetto dell’attrazione reciproca tra Luna e Terra e le
conseguenti sollecitazioni gravitazionali sulle masse degli oceani.
Questo si è potuto riscontrare solo dopo la realizzazione di orologi di
precisione assoluta (anni ’50), basati sul conteggio delle oscillazioni di
atomi di cesio, confrontando rispetto ad essi la durata del giorno
astronomico; per ora il ritardo misurato del giorno astronomico rispetto a
quello “atomico” è di circa 35 secondi ).
Quali erano i fenomeni che potevano osservare gli antichi? (fate anche
riferimento alle figure della Lezione 10):
La durata dell’arco diurno e di quello notturno non erano costanti
nel corso delle stagioni; tuttavia, nell’arco di uno stesso giorno,
gli intervalli di tempo tra alba ed passaggio del sole al meridiano
superiore (che indica la direzione del sud) e tra meridiano
superiore e il tramonto erano sempre uguali;
Il passaggio del sole al meridiano superiore (che coincide anche
con il raggiungimento della massima altezza dell’astro nel cielo
nel corso di una giornata) poteva quindi esser preso come metà
della giornata, cioè “mezzogiorno”;
Analogamente, dopo aver posizionato opportuni traguardi di
riferimento, (Stonehenge? Templi mesopotamici ed egizi?) si
poteva osservare il passaggio ai meridiani superiore/inferiore
(verso sud/verso nord) del Sole di giorno o di determinate stelle
di notte ed avere quindi una sorta di misura dello scorrere del
tempo;
Un approccio ancora più sofisticato aveva consentito di
sviluppare il concetto di meridiana, che non solo poteva dare
indicazione dell’ora durante la giornata, ma anche indicazione del
periodo dell’anno, in base al variare della lunghezza dell’ombra
di una struttura fissa, proiettata dal Sole a mezzogiorno; peraltro
si poteva notare che l’altezza delle stelle, che sono “fisse” sulla
sfera celeste, risultava sempre costante, nel corso dell’anno, al
loro passaggio sul meridiano inferiore (non quella dei pianeti e
della Luna);
Abbastanza presto era nato il concetto di Equinozio (in tale
giorno, oltre ad una durata dell’arco diurno uguale a quella della
notte, a tutte le latitudini il Sole sorge sempre ad Est e tramonta
sempre ad Ovest); questo consentiva di individuare la durata di
un anno; vale a dire il numero di giorni che intercorrevano tra
due successivi equinozi di primavera (365);
Nel corso di un anno, tutte le osservazioni astronomiche,
avvenute nel corso dell’anno precedente, si ripetevano
esattamente (posizione del sole all’alba ed al tramonto, altezza
del sole a mezzogiorno, sorgere e tramonto degli astri)
Proseguendo nello sviluppo delle cognizioni sullo scorrere del
tempo, si venne a suddividere la durata del giorno in ventiquattro
parti, cioè in ore, e quella di un anno in dodici mesi (pur
risultando irrealizzabile il tentativo di far coincidere la durata del
mese con quella dell’orbita lunare che dura circa 29 giorni).
Mancavano tuttavia strumenti precisi per “amministrare” con
precisione lo scorrere del tempo nell’arco della giornata, tra un
passaggio in meridiano e l’altro ( la clessidra era l’unico
strumento a disposizione)
Ma del resto nella vita di tutti i giorni l’esigenza di avere una misura
precisa del tempo ,oltre che non realizzabile, non era in fondo molto
sentita.
Chi aveva l’esigenza di misurare in maniera precisa i minuti ed i secondi?
La tecnologia per addivenire a metodi di misura più precisi cominciò ad
essere sviluppata con l’avvento della scienza moderna:
Galileo elaborò le leggi dell’isocronia delle oscillazioni del pendolo
e rese quindi possibile lo sviluppo di orologi meccanici;
La necessità di effettuare sperimentazioni nel campo della
cinematica e della meccanica rese necessario lo sviluppo di ulteriori
tecniche per realizzare orologi meccanici, basati sulla isocronia delle
oscillazioni di bilancieri a molla (progenitori dei moderni orologi);
L’esigenza sempre più pressante di disporre di misure del tempo
riferibili al moto apparente delle stelle, dopo l’invenzione dei
cannocchiali e dei telescopi astronomici, motivò la creazione dei
primi osservatori astronomici dedicati alla misura del tempo,
mediante l’osservazione del passaggio degli astri al meridiano;
Lo sviluppo della scienza della navigazione, divenuta necessaria per
la navigazione oceanica, portò finalmente ( XVIII secolo) allo
sviluppo del cronometro marino che riusciva a fornire l’ora con
errore giornaliero costante di pochi secondi – tale è la precisione
richiesta per la determinazione della longitudine mediante le
osservazioni astronomiche in mare;
A partire dall’invenzione della radio fu possibile, per gli osservatori
astronomici basati a terra, trasmettere i segnali orari di precisione
alle navi in oceano, consentendo così la verifica giornaliera
dell’errore dei cronometri imbarcati;
Con la realizzazione degli orologi al quarzo, la precisione della
misura del tempo a bordo divenne completamente indipendente e
rispondente alle esigenze di precisione per la determinazione del
punto nave mediante osservazione astronomica in oceano;
Infine la realizzazione di orologi sincronizzati dalle oscillazioni di
particolari atomi (ad es. cesio) ha consentito di ottenere precisioni
dell’ordine del milionesimo di secondo;
La realizzazione di satelliti artificiali (Global Positioning System)
dedicati alla navigazione ha infine completamente svincolato i
naviganti dall’esigenza di riferirsi alla posizione degli astri per
determinare la posizione in mare. (ne parleremo a fondo in un
capitolo dedicato).2. il tempo locale sui meridiani – il tempo sul meridiano di Greenwich
Dopo questa premessa “storica”, è opportuno consolidare una chiara
visione sul problema della misura del tempo, come bagaglio intellettuale
per sentirsi a proprio agio nel contesto della navigazione, nella quale siamo
osservatori consapevoli degli eventi astronomici, così come di quelli
meteorologici.
Innanzitutto è opportuno definire il concetto di ora locale.
In ogni posizione geografica, caratterizzata da una specifica longitudine,
l’ora locale è riferita al passaggio al meridiano superiore del Sole (preso a
riferimento già dagli antichi il Sole).
Abbiamo però visto che il Sole, pur essendo stato il riferimento storico
iniziale, non è contraddistinto da un regolare passaggio al meridiano, in
quanto il suo movimento apparente nella sfera celeste è il risultato del
movimento diurno di rotazione della Terra intorno al suo asse, come per le
stelle fisse, ma anche del movimento annuale di rivoluzione della Terra
intorno al Sole.
La Terra compie un’orbita ellittica intorno al Sole, che occupa uno dei due
fuochi dell’ellisse (vedi leggi di Keplero), di conseguenza il suo moto di
rivoluzione risulta variamente accelerato (più veloce quando è più vicina al
Sole e più lento quando ne è lontana), tanto da far risultare irregolare il
moto apparente del sole sulla fera celeste.
Fu la necessità di comprendere la ragione di queste irregolarità, insieme a
quelle dei pianeti e della Luna, che spinsero Keplero a sviluppare le leggi
della meccanica celeste, che davano piena rispondenza alle osservazioni
sul movimento sulla sfera celeste del sole e dei pianeti nel corso dell’anno.
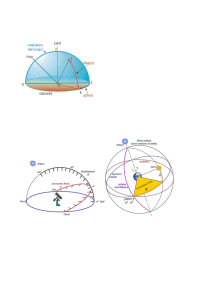
Osserviamo la figura seguente, già esposta nella lezione….:
questa figura è la rappresentazione della sfera celeste, per un osservatore
posizionato nell’emisfero nord, ad una latitudine di circa 60°; la
longitudine non è specificata e la figura vale per tutti gli osservatori che si
trovano a quella latitudine (la verticale dell’osservatore è rappresentata in
blu, così come la linea dell’orizzonte);
I poli Nord e Sud “celesti” sono determinati dall’intersezione tra la
sfera e l’asse di rotazione, che ha origine nel centro della sfera
(ricordiamo che in questa rappresentazione il centro della Terra e
della sfera celeste coincidono e la Terra è considerata puntiforme in
relazione alle dimensioni “infinite” della sfera celeste)
Sul piano dell’orizzonte dell’osservatore, la sua intersezione con il
piano dell’equatore celeste, è indicata con una linea tratteggiata blu
che incontra la sfera in corrispondenza della direzione dei punti
cardinali Est ed Ovest
Il meridiano superiore è il semicircolo massimo, passante per i poli,
che contiene lo Zenith, il punto Q ed il punto cardinale Sud; il
meridiano inferiore è il semicircolo massimo che contiene il punto
Q’, il Nadir ed il punto cardinale Nord;
Abbiamo già visto che gli astri, “incastonati” nella sfera celeste, si
muovono con essa (percorrendo paralleli più o meno distanti
dall’equatore in relazione alla loro declinazione celeste e
raggiungono il culmine della loro ascesa diurna quando passano in
corrispondenza del meridiano superiore Q;
Immaginiamo anche che l’osservatore si trovi sul meridiano zero, quello di
Greenwich.
Esaminiamo adesso la successiva figura 2, ottenuta proiettando la
precedente rappresentazione sul piano passante per l’equatore celeste;
l’equatore, sul quale giacciono i punti Q e Q’, è rappresentato dal cerchio;
il punto Z è la proiezione dello Zenith sul piano dell’equatore, il punto G è
l’analoga proiezione dello zenith di Greenwich; la longitudine
dell’osservatore è uguale a quella di Greenwich, cioè zero :
La freccia gialla indica il senso effettivo di rotazione della terra (senso
antiorario); di conseguenza il movimento apparente della sfera celeste e
degli astri è in senso contrario (senso orario)
La direzione del moto apparente del sole e di una stella sono mostrati
dalle relative frecce, così come quello del punto
(ricordiamo che il
punto è originato dall’intersezione dell’eclittica con l’equatore, la sua
posizione è stata assunta come origine delle coordinate celesti degli
astri e quindi la sua declinazione e la sua coascensione retta co sono
zero);
Definizione: L’angolo compreso tra il piano passante per il
meridiano superiore (in questo caso il meridiano zero di Greenwich)
ed il piano giacente sull’asse della sfera celeste e contenente la
posizione del centro del sole è denominato angolo orario del sole
vero ed indicato con Tv ; analogamente viene definito l’angolo
orario di una stella (indicato con Ta) e l’angolo orario del punto
(indicato con Ts);
L’angolo orario è misurato in senso orario da 0° a 360° a partire dal
punto Q fino al punto in cui il meridiano passante per l’astro taglia
l’equatore; se espresso in ore (da 0h a 24h), la misura avviene a
partire dal punto Q’ (meridiano inferiore)
Dalla figura 2 si vede come l’angolo orario di ogni astro può essere
espresso come la somma dell’angolo orario del punto
coascensione retta dell’astro stesso;
e della
Tv = Ts + co sole
Ta = Ts + co
gli osservatori astronomici possono rilevare con estrema precisione
il momento del passaggio del centro del sole al meridiano superiore e delle stelle al meridiano inferiore -, e determinano periodicamente
l’ora locale, verificando gli errori sistematici e di marcia degli
orologi di riferimento utilizzati per la trasmissione del segnale orario
in particolare per l’osservazione del sole, bisogna tenere conto che
nel corso dell’anno solare, la sua posizione apparente risente del
moto variamente accelerato della Terra sulla sua orbita di
rivoluzione intorno al Sole;
viene perciò utilizzato un sole immaginario (sole medio)
caratterizzato da un moto apparente sull’eclittica uniforme nel corso
dell’anno; la differenza tra il passaggio del sole vero al meridiano
superiore e del sole medio (che rappresenta l’ora astronomica), può
essere calcolata analiticamente “a priori” (mediante le equazioni di
Keplero), e viene detta “equazione del tempo”, il cui simbolo è v;
dopo aver osservato l’ora Tv dell’effettivo passaggio del Sole al
meridiano zero, essa viene corretta per il movimento non uniforme
della Terra sulla sua orbita, ricavando il tempo medio di riferimento
Tm, mediante la relazione :
Tm = Tv + v
Il valore calcolato dell’equazione del tempo nel corso dell’anno
solare è indicativamente riportato nel grafico successivo (fig. 3), che
mette in evidenza l’anticipo od il ritardo del passaggio del Sole al
meridiano rispetto all’ora effettiva (i valori esatti sono riportati sulle
Effemeridi)
Il sole vero quindi anticipa o ritarda il suo passaggio al meridiano
rispetto al sole medio; nel corso dell’anno la differenza v si annulla
quattro volte.
Per esempio, a metà Febbraio il Sole arriverà in ritardo di circa 14
minuti rispetto al Tempo medio di Greenwich e a metà Novembre,
esso sarà in anticipo di circa 16 minuti.
Poiché l’equazione del tempo rimane pressoché invariata nel corso
della stessa giornata, il ritardo (o l’anticipo) verificato sul meridiano
zero si riscontra anche al passaggio del Sole su tutti gli altri
meridiani;
Per accordo internazionale, il tempo medio di Greenwich è stato assunto
come ora di riferimento a livello mondiale; tuttavia, con l’avvento degli
orologi “atomici”, il metodo di controllo astronomico dell’ora di
riferimento è passato in seconda linea di importanza.
Consiglio agli appassionati, in caso di viaggio a Londra, di spendere una
mattinata per una visita all’osservatorio di Greenwich (c’è anche un
interessante museo sulla storia della navigazione e la mostra dei cronometri
marini), magari arrivandovi con un battello sul Tamigi, anziché ricorrere
alla metropolitana sotterranea.
L’angolo orario tv, detto anche “ora locale dell’astro”, contraddistinto
dalla t minuscola, è sempre riferito al meridiano geografico
dell’osservatore; da notare che nello stesso istante, osservatori posizionati
su meridiani diversi, misurano angoli orari differenti dello stesso astro; la
differenza tra le misure è data dalla differenza di longitudine tra gli
osservatori.
Ciò viene messo in evidenza nella figura seguente:
l’intersezione del meridiano di Greenwich con l’equatore celeste è
indicato dal punto G; il punto Q indica analogamente il meridiano
dell’osservatore
l’angolo compreso tra i punti G e Q è la longitudine
dell’osservatore; nel caso rappresentato in figura, l’osservatore si
trova ad Est rispetto al meridiano zero (segno della longitudine “+”);
la relazione (1) mostra il legame tra angolo orario del punto
rispetto al meridiano di Greenwich e l’angolo orario del sole
indicato con la freccia rossa tratteggiata;
la relazione (2) mostra il legame tra l’angolo orario del Sole tv
rispetto all’osservatore e l’angolo orario Tv riferito al meridiano
zero;
ciò indica che uno evento astronomico (ad esempio il passaggio del
sole al meridiano dell’osservatore) viene contraddistinto da un ora
locale legata al meridiano dell’osservatore e dall’ora locale di
Greenwich; la differenza tra i due angoli orari è pari alla longitudine
dell’osservatore (con il suo segno: Est positiva – Ovest negativa);
il tempo medio del passaggio in meridiano del sole è legato alla
longitudine dell’osservatore ed all’equazione del tempo come
indicato nella relazione (4)
Vediamo ora come la differenza di longitudine e la velocità di rotazione
della sfera celeste si correlano, per due osservatori posizionati in
longitudini diverse, all’ora locale in cui avviene un stesso evento
astronomico : ad esempio il tramonto di una stella (ma potrebbe essere il
passaggio del sole al meridiano superiore, il sorgere del sole, il passaggio
al meridiano inferiore di una stella).
Commentiamo la figura 5 :
supposta, per comodità grafica, uguale a zero la declinazione della
stella, il punto Q1 è il piede sull’equatore celeste del meridiano
superiore dell’osservatore 1, di cui volutamente non è specificata la
latitudine (il ragionamento è valido per tutti gli osservatori che
hanno la stessa longitudine 1); Q2 è il piede del meridiano
superiore di tutti gli osservatori di longitudine 2;
posti nell’esempio l’angolo orario dell’astro t1, riferito al meridiano
1, pari a 90°, e la differenza di longitudine +30° si vede che t2 è
120°;
per tutti gli osservatori di longitudine 1, la stella è al tramonto
(l’affermazione “tutti” è valida solo quando la declinazione della
stella è zero); per gli osservatori posti sul meridiano di longitudine
2 la stella è già tramontata da 2 ore;
la velocità di rotazione della sfera celeste in senso orario da Est
verso Ovest (uguale e contraria a quella della Terra) è di :
360°/ 1 giorno = 360°/24h = 15°/ 1h = 1°/ 4m
questa osservazione, insieme alla relazione (3) della figura 5, ci fa
vedere come gli eventi astronomici avvenuti (o che avverranno) su
un determinato meridiano, sono già avvenuti (o avverranno) dopo un
tempo pari alla differenza di longitudine espressa in ore (attenti al
segno della longitudine e della differenza !!!!);
analogamente se t1 è l’ora locale (l’angolo orario) del passaggio di
un astro al meridiano superiore, per osservatore di longitudine 1,
l’angolo orario t2 dello stesso astro, misurato nello stesso istante, è
uguale a t1 +
(attenti al segno della longitudine e della differenza !!!!)
ESERCIZIO 1: passaggio in meridiano di un astro (declinazione celeste
5°sud) per un osservatore in latitudine 20°S e longitudine 1=45°W :
angolo orario t1 = 12h = 000°;
DOMANDA: determinare il corrispondente angolo orario per un
osservatore su longitudine 2=100°E e latitudine 30°N e per l’osservatorio
di Greenwich (51°28’38’’N-0°00’00’’)?
RISPOSTA:
1) la latitudine è ininfluente sulla misura dell’angolo orario
2) la declinazione dell’astro è ininfluente per l’istante del passaggio in
meridiano
3) l’angolo orario locale dell’osservatore 2 è :
t2 = t1 + 0°00’ + [100°E-45W] = 0°00’ + [+100°- (- 45°)]
=0°00’ + [145°] = 145° = 9h 40m + 12h = 21h 40m
(l’astro era già passato 9 ore e 40 minuti prima al meridiano
dell’osservatore 2)
4) l’angolo orario calcolato per l’osservatorio di Greenwich è :
T = t1 + 0°00' + [00° - 45°W] = 0°00’ + [00° - ( -45°)]
= 00° + [ +45°] = +45° = 3h + 12h = 15h 00m
(l’astro era già passato al meridiano di Greenwich 3 ore prima)
ESERCIZIO 2: Osservatore 1 (10°00’N – 150°00’E);
Osservatore 2 (5°00’S° - 100°30’W)
Data : 21 marzo
DOMANDA : determinare l’ora locale del sorgere del Sole per entrambi
gli osservatori, quale osservatore lo vedrà sorgere per primo e dopo quanto
tempo lo vedrà sorgere il secondo
RISPOSTA :
1) il 21 marzo è il giorno dell’equinozio di primavera, la declinazione
del Sole è zero; l’arco diurno è esattamente uguale a quello notturno;
il sorgere di un astro posizionato sull’equatore celeste avviene alla
stessa ora locale t per tutti gli osservatori a qualsiasi latitudine
(t=270° = 6h 00m)
2) l’osservatore 2 (long. 100°30’W) vedrà per primo il sorgere del Sole,
al suo tempo locale t2 = 270° = 06h00m; in quel momento è ancora
notte per l’osservatore 1;
3) l’osservatore 2 vedrà sorgere l’astro alle sue 06h 00m locali; la
differenza di longitudine è = 2 - 1 = 100°30’W – 150°00’E
= - 100°30’ – 150°00’ = -250°30’ = +(360° - 250°30’)= +109°30’
che la sfera celeste dovrà compiere nel suo moto rotazione diurna
per far arrivare il Sole all’orizzonte dell’osservatore 1 ;
4) ciò corrisponde ad un tempo t di 7h 18m ;
l’osservatore 1 vedrà sorgere il sole 7h18m dopo l’osservatore 2, al
suo tempo locale t1 = 06h00m