Inferenza statistica

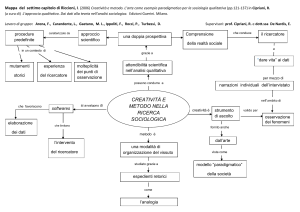
Concetti di base della ricerca scientifica e
Inferenza statistica
Go back to page: Test parametrici
[L'indagine empirica] [tipi di variabili e modi di trattarle] [validità delle indagini empiriche]
[i più comuni disegni di ricerca]
[significatività statistica delle conclusioni]
L'indagine empirica
Il procedimento scientifico in psicologia e in psicopedagogia ha come obiettivo descrivere, predire,
spiegare il comportamento e le relazioni regolari tra i vari aspetti del comportamento stesso. Un
comportamento che per gli insegnanti è importante è l'apprendimento, ad esempio.
Tutte le ricerche partono sempre da un quesito derivante:
1) da un'osservazione
2) da una lacuna in una teoria
e tale questito guida l'intera ricerca. Per poter procedere verso una descrizione o spiegazione di un
evento (di apprendimento, ad esempio) il ricercatore deve trasformare il quesito in una ipotesi di
ricerca. Essa è quindi un tentativo di spiegazione dell'evento ed è formulata secondo uno schema:
"se….allora….".
Per esempio il quesito: "Perché alcuni alunni si comportano in modo aggressivo?" potrebbe
diventare l'ipotesi di ricerca: "Se un alunno è frustrato allora si comporta in modo più aggressivo di
un individuo che non lo è" o altre analoghe.
L'ipotesi deve però essere verificabile. Una ipotesi può non essere verificabile se
1) mancano le definizioni dei concetti implicati (ex: manca la definizione di aggressività)
2) l'ipotesi stessa è circolare ove l'evento è usato come spiegazione di se stesso (se i bambini sono
aggressivi, allora si sentono ostili)
3) si fa uso di concetti che non possono essere verificati (ex: se qualcuno è aggressivo è a causa
del suo segno zodiacale).
Le ipotesi quindi devono
a) fondarsi su definizioni operative delle caratteristiche che sono oggetto di studio.
b) Il ricercatore deve essere consapevole che possono esserci più definizioni operative dello stesso
concetto (ex: apprendimento)
c) Il ricercatore si pone in atteggiamento critico rispetto al risultato del proprio lavoro: cioè deve
essere convinto che la spiegazione ottenuta è la più probabile rispetto alle altre spiegazioni
possibili.
d) Il ricercatore deve avere chiaro fin dall'inizio che tipo di relazione ipotizza fra i concetti oggetto
di studio. La relazione fra i concetti può essere di tipo causale (x è causa di y) o di tipo
correlazionale (x e y si presentano insieme nell'evento comportamentale).
e) Se il ricercatore ha come obiettivo di limitarsi a fornire una rappresentazione il più possibile
accurata di ciò che avviene, allora la sua indagine empirica sarà a livello descrittivo.
f) Se il ricercatore ipotizza una compresenza sistematica in uno stesso evento, dei concetti
studiati, il livello dell'indagine sarà correlazionale (ex: tutoring e apprendimento).
g) Se il ricercatore ha come obiettivo di spiegare il comportamento in funzione di un'unica causa,
allora la sua indagine sarà sperimentale ed è il più elevato livello di indagine. Il ricercatore
ipotizza una relazione di causa ed effetto fra x e y.
Indagine sperimentale = x e y sono in relazione di causa ed effetto
Indagine correlazionale = x e y si presentano insieme nel comportamento
Indagine descrittiva= descrizione del comportamento e di x e y
Tipi di variabili e modi di trattarle:
Si definisce variabile qualsiasi attributo o caratteristica che può cambiare e variare, cioè può
assumere valori diversi o categorie diverse: ex: altezza, socievolezza, reddito, tipo di religione, etc.
Se un attributo non varia si definisce costante: ex il numero delle teste o dei cuori in un individuo è
una costante. Se si è interessati a studiare i ragazzi di 16 anni, anche l'età diventa una costante.
Modo di trattare le variabili:
1) Modo X: si tiene la variabile che interessa sotto controllo, facendole assumere solo determinati
valori noti al ricercatore. E' la variabile indipendente.
2) Modo Y: consiste nel far variare liberamente la variabile e registrare i valori che assume
(variabile dipendente)
3) Modo K: consiste nel mantenere costante una variabile rilevante per l'indagine. Solitamente il
ricercatore cerca di trattare in modo K le variabili di disturbo che potrebbero influire sui risultati
ma che non sono direttamente rilevanti per l'indagine. L'età potrebbe essere tipicamente una
variabile di disturbo, ma anche l'avvicendamento di diversi insegnanti in una stessa classe etc.
4) Modo M: quando non è possibile trattare le variabili di disturbo nel modo K il ricercatore cerca
di eliminarne i possibili effetti costruendo dei sottoinsiemi di soggetti nei quali la /le variabili di
disturbo siano presenti in eguale misura. Il modo M (da matching) consiste nel misurare la
variabile creando dei sottoinsiemi nei quali la variabile stessa è presente in maniera analoga. Ex.
Se supponiamo che l'età dei soggetti sia una variabile di disturbo, invece di trattare la variabile
nel modo K, cioè prendere soggetti della stessa età, una volta rilevata l'età dei soggetti possiamo
creare gruppi composti di individui delle stessa età ed assegnmare a caso un individuo al gruppo
sperimentale ed uno al gruppo di controllo.
5) In base al livello di misura che viene adottato, le variabili si distinguono in:
A) variabili discrete (categoriali o nominali o mutabili)
B) variabili continue
La validità delle indagini empiriche:
Si definisce validità "la migliore approssimazione disponibile alla verità" (Cook & Campbell,1979):
ve ne sono di 4 tipi:
1) validità interna
2) validità esterna
3) validità statistica delle conclusioni
4) validità di costrutto (delle procedure di manipolazione e di misura delle variabili)
1) Validità interna: di una ricerca è il grado con cui le conclusioni che vengono tratte sono
riferibili effettivamente alla relazione fra le variabili in gioco e non ad altro. E' il grado di
certezza con il quale il ricercatore può escludere interpretazioni alternative alle sue conclusioni.
2) Validità esterna: riguarda la possibilità di estendere i risultati dell'indagine ad altri soggetti in
luoghi diversi in tempi diversi. Essa è legata al campionamento dei soggetti. Se il campione è
rappresentativo della popolazione, allora la validità esterna è elevata.
3) Validità delle conclusioni statistiche: riguarda la probabilità che la relazione tra la variabile
indipendente (il tipo di insegnamento) e quella dipendente (apprendimento) sia effettiva e non
dovuta al caso.
4) Validità di costrutto: deriva dalla capacità del ricercatore di definire in termini operativi le
variabili rilevanti per l'indagine.
I più comuni disegni di ricerca:
Disegni sperimentali: consentono al ricercatore il massimo grado di interpretabilità dei risultati
poiché lo sperimentatore ha un controllo completo della variabile che assume il ruolo di causa (il
tutoring o la lezione frontale). Tale variabile dovrà assumere almeno due valori (variabile
dicotomica) assenza/presenza o modalità, che corrisponde al controllo/trattamento, e che i soggetti
vengono assegnati a caso a ciascuna delle due modalità della variabile (alla lezione frontale o al
tutoring). Nel disegno sperimentale più elementare è presente una prima misura della variabile
dipendente rilevata prima dell'esperimento (grado di profitto nella materia X) (pre-test), e una
seconda misura rilevata dopo l'esperimento (post-test) sia per il gruppo che ha avuto il trattamento,
sia per il gruppo di controllo. Il disegno sarà del tipo:
R
VD
O1
VI
SI
VD
O2
R
O3
NO
O4
Gruppo
sperimentale
Gruppo di
controllo
Dove R (random) sta ad indicare che i soggetti sono assegnati a caso alle due condizioni
sperimentali, presenza (SI) e assenza (NO) del trattamento. Il ricercatore è interessato a trovare una
differenza fra O2 e O4 in modo da poter attribuire tale effetto alla causa "trattamento" (tutoring):
questo purchè non esistesse già una differenza fra O1 e O3.
Un buon disegno sperimentale deve:
a) prevedere un gruppo di controllo o una condizione di controllo e
b) assegnare a caso i soggetti alle condizioni sperimentali. Se quesat condizione b) non può essere
rispettata e si devono usare gruppi "già precostituiti" o già esistenti al momento della
sperimentazione (una classe di alunni ed esempio) allora si ha un disegno quasi-sperimentale.
Nella pratica i disegni di ricerca sono molto complessi e spesso si trovano nello stesso disegno variabili sperimentali e
variabili quasi sperimentali (questo succede quasi sempre nei disegni di ricerca psicopedagogica): non esiste una
gerarchia assoluta tra i disegni di ricerca, sta al ricercatore decidere, in funzione del tipo di indagine che si propone,
quale disegno adottare in relazione al massimo controllo possibile che può esercitare sulle variabili in gioco.
La significatività statistica delle conclusioni:
Per poter applicare tecniche statistiche ai dati raccolti bisogna definire prima anche le ipotesi
statistiche, tradurre cioè l'ipotesi di ricerca in ipotesi suscettibili di verifica in base alla teoria
statistica. La verifica probabilistica delle ipotesi è un insieme di procedure inferenziali che,
partendo da dati rilevati su campioni, consente di prendere delle decisioni sulla popolazione,
consente cioè di generalizzare i risultati ottenuti dal campione alla popolazione di provenienza
del campione medesimo.
L'ipotesi statistica si esprime in:
IPOTESI NULLA (H0) = Gli effetti della variabile indipendente sono nulli (ex: gli effetti della
lezione frontale sono nulli)
IPOTESI ALTERNATIVA (H1) = la variabile indipendente ha avuto un effetto di generica
differenza tra i due gruppi (ipotesi bidirezionale), o ha avuto un effetto specifico (ipotesi
monodirezionale), nel senso che ci si aspetta che sul gruppo sperimentale abbia avuto l'effetto di
aumentare o diminuire la prestazione.
La parte della statistica che si occupa della verifica probabilistica delle ipotesi viene detta
statistica inferenziale poiché dalle caratteristiche di un campione si cerca di inferire le caratteristiche della
popolazione dalla quale si presume che il campione provenga.
L'insieme delle procedure che usano i dati del campione per stabilire la credibilità dell'ipotesi di
ricerca sulla popolazione viene detta : verifica delle ipotesi.(torna a Esperimenti su singoli)
La verifica delle ipotesi viene fatta sulla base delle distribuzioni campionarie dei test statistici che il
ricercatore sceglie come più appropriati al suo caso.
Per esempio, nella ricerca sugli effetti dell'induzione di sentimenti di cooperazione (atteggiamenti
prosociali) sulla generosità dei soggetti, il ricercatore può scegliere la statistica "media" per
sintetizzare la variabile dipendente del suo esperimento ed è interessato a valutare se la differenza
riscontrata tra le medie calcolate sui due gruppi di soggetti (sperimentale e di controllo) può essere o
meno dovuta al caso. Per poter prendere una tale decisione il ricercatore ha bisogno di una
distribuzione campionaria del test statistico che sceglierà per valutare la differenza.
Una distribuzione campionaria è una distribuzione teorica di frequenze relative ad una certa
statistica (per esempio una media) che viene costruita assumendo di aver estratto un numero
infinito di campioni di una certa numerosità da una popolazione e di aver calcolato le
statistiche su ciascuno di essi.
L'insieme di tali statistiche sarà rappresentabile in una distribuzione di frequenze che viene
appunto chiamata distribuzione campionaria di quella statistica e che avrà in ascissa i diversi
valori che la statistica può assumere ed in ordinata le probabilità di occorrenza di ciascuno di
essi. Esistono distribuzioni campionarie note di varie statistiche come:
1)medie
2)varianze
3)proporzioni
4)differenze fra medie
5)correlazioni
6)la t di Student
7)la F di Fischer
8)il Chi2 (2) ed altri ancora….
All'interno di queste distribuzioni il ricercatore stabilirà il livello di significatività che di solito viene
chiamato  e corrisponde all'errore che il ricercatore accetta di fare nel trarre le conclusioni: un
livello di significatività del 5% ( =.05) significa che il ricercatore accetta di poter sbagliare 5
volte su 100 nel considerare significativa una differenza che non lo è.
L'area sottesa alle distribuzioni campionarie è resa uguale a 1 perciò se  =.05, la rimanente area
sarà pari a .95; la distribuzione campionaria è così divisa in due regioni, la regione di rifiuto e la
regione di accettazione dell'ipotesi nulla. Il valore della statistica che divide le due regioni viene
chiamato valore critico.
Fig.1
H0
H1
Xmedia
Si può dire che il test è un procedimento che permette di giungere probabilisticamente ad un giudizio
riguardante la validità di una ipotesi. Consideriamo il caso - per esemplificare - in cui si voglia
verificare l'efficacia di un certo metodo di insegnamento sull'apprendimento.
E' opportuno utilizzare un campione costituito da un numero N di osservazione. In una fase che
precede l'esecuzione dell'esperimento, il ricercatore formula due ipotesi (due ipotesi semplici - per il
momento) escludentisi fra loro. La prima H0 è l'ipotesi nulla: l'intervento non ha efficacia. La
seconda H1: l'intervento ha efficacia. Tali ipotesi corrispondono al altrettante popolazioni
alternative da cui si suppone possa essere estratto il campione. Si tratta di determinare, sulla base
dei risultati dell'esperimento per campione, a quale ipotesi dare credito, cioè quale popolazione
ritenere abbia generato il campione. I soggetti, costituenti il campione presentano un rendimento
medio Xmedio che può essere uno dei valori appartenenti alla distribuzione della media
campionaria sotto l'ipotesi H0, prima dell'intervento, o dopo in caso di inefficacia, oppure alla
distribuzione H1 in caso di efficacia. (Fig1)
Il ricercatore, come si nota in Fig1. Difficilmente potrà stabilire di quale distribuzione campionaria
(ipotesi) fa parte il campione. Pertanto, nell'incertezza, per decidere se l'intervento è efficace o
meno, stabilisce di fissare un punto o valore critico Pc sull'asse delle ascisse, che delimita due zone:
Fig.2
Fig.2
H0
H1
1 -
1 -


Zona di accettazione di H0
Zona di rifiuto di H0
La linea vericale è la linea del valore critico.
L'asse delle ascisse rimane divisa in due zone: una di accettazione ed una di rifiuto di H0. il
ricercatore. Se il campione estratto risulta appartenere alla zona di rifiuto, respingerà H0 a favore di
H1, se appartiene alla zona di accettazione, accetta H0. IL rischio di sbagliare esiste, ma si tratta di
scegliere il margine di errore di questo rischio. Ci possono essere due tipi di errori:
Stato del problema (che non conosciamo)
decisione
Accettiamo H0
Respingiamo H0
ipotesi nulla è vera
corretto
Errore I tipo
Ipotesi nulla è falsa
Errore II tipo
corretto
Si definisce errore del primo tipo quando respingiamo l'ipotesi nulla quando è vera.
Si definisce errore di II tipo quello che si commette accettando l'ipotesi nulla quando è falsa. La
probabilità di commettere errori di II tipo è legata alla potenza dell'analisi statistica. In realtà il
ricercatore è interessato non tanto a scoprire se è vera l'ipotesi nulla, ma a falsificarla, cioè a
dimostrare che essa è falsa e che la variabile indipendente (il trattamento) ha avuto effetto. Il
ricercatore è interessato a respingere correttamente l'ipotesi nulla. La probabilità corrispondente
viene chiamata potenza ed indicata con
(1 - ) dove  è la probabilità di commettere un errore di II tipo.
Accettiamo H0
Ipotesi nulla è vera:
( 1- ) 95%
Respingiamo H0
Errore di I tipo
 5%
L'ipotesi nulla è falsa
Errore di II tipo
 20%
Corretto
( 1-) 80% potenza
Le distribuzioni campionarie vanno, oltre che in funzione dello specifico test statistico (la
distribuzione normale, la distribuzione della t di Student, la distribuzione del 2 di Poisson, la
distribuzione della F di Fischer etc) anche in funzione dei gradi di libertà della statistica specifica.
Per decidere se accettare o respingere l'ipotesi nulla il ricercatore deve confrontare il valore della
statistica calcolato sui suoi dati con il valore critico previsto al livello di significatività prescelto: se
il valore trovato è superiore al valore critico esso si troverà nella regione di rifiuto e potrà
respingere l'ipotesi nulla e accettare l'ipotesi alternativa.
quasiesper.doc