Frazioni e numeri decimali
Numeri decimali :
I numeri decimali sono formati da una parte intera e una parte
frazionaria che sono separati da una virgola :
ES.
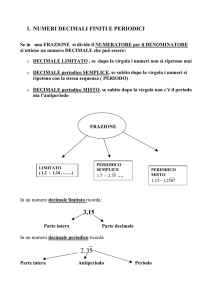
307 , 1024
PARTE INTERA PARTE FRAZIONARIA
Frazione decimale:
Una frazione decimale è una frazione che ha come denominatore una
potenza del 10.
Es : 21/1000 ; 156/10000; 4/10…….
Unità decimale :
l’unità decimale è una frazione che ha come numeratore 1 e come
denominatore 10 o una sua potenza .
Es: 1/ 10 ; 1/100; 1/1000; 1/104 ; 1/105
Una frazione può essere scritta anche come il prodotto tra un numero intero e
un’unità decimale come nell’esempio.
Es : 372 = 300+70+2 = 300 + 70 + 2 = 3 • 1 + 7• 1 + 2 • 1
1000
1000
1000 1000 1000
10
100
1000
Da una frazione a un numero decimale :
Per trasformare una frazione in numero decimale basta divedere il
numeratore per il denominatore:
a/b = a:b
il quoziente può essere : • Finito: quando il quoziente della frazione dopo la
virgola ha cifre finite . ( decimale limitato )
• Periodico: quando il quoziente della frazione dopo la
virgola ha cifre infinite . (decimale periodico)
numeri decimali periodici:
I numeri decimale periodici sono numeri composti da:
•
La parte intera cioè tutte le cifre che precedono la virgola
•
L’antiperiodo cioè le cifre che non si ripetono con una sequenza , questo è
posizionato dopo la virgola, tra la parte intera e il periodo.
•
Il periodo cioè tutte le cifre che si ripetono con una precisa sequenza all’infinito, esso
è posizionato dopo l’antiperiodo
In casi particolari i numeri che dopo la virgola si ripetono all’infinito non sono divisi tra
antiperiodo e periodo, ma c’è solo l’antiperiodo, cioè dopo la virgola troviamo tutte
cifre che non si ripeteranno mai con una sequenza , questo si verifica solo per numeri
che non fanno parte di Q cioè i numeri irrazionali.
Parti di un numero periodico:
124, 71935353535353535353 ….
parte intera
antiperiodo
periodo
Definire se un numero decimale è periodica o finita:
per definire se un numero decimale è periodico o finito dobbiamo
prendere in considerazione la frazione da cui proviene e scomporre il
denominatore:
•
se i fattori primi sono solamente 2 o 5 o entrambi allora il numero decimale è finito .
Es. 3/ 25 scomp . In fatt. primi : 25 = 5•5 , 5 è tra i fattori primi quindi il numero
decimale sarà finito.
•
Se i fattori primi sono diversi da 2 o 5 allora il numero decimale sarà periodico .
Es. 5/21 scomp. In fatt. primi : 21= 3•7 , ne 5 ne 2 fanno parte dei fattori primi quindi il
numero decimale sarà periodico .
Da un numero decimale alla frazione :
1° CASO : Numero decimale FINITO
Per passare da un numero decimale finito a una frazione bisogna mettere al
numeratore tutto il numero senza la virgola e al denominatore 10 o 100 o 1000 a
seconda di quante sono le cifre dopo la virgola , quindi metteremo tanti zeri
quanti sono i numeri dopo la virgola.
ES. 1, 23 = 123
100
a = numero senza la virgola
b = 10, oppure 100, oppure 1000
2° CASO: Numero decimale PERIODICO
Per passare da un numero decimale periodico a una frazione bisogna mettere al
numeratore la differenza tra il numero scritto senza la virgola e il numero scritto
senza il periodo, al denominatore bisogna mettere tanti 9 quanti sono le cifre del
periodo , seguiti da tanti 0 quanti sono le cifre dell’antiperiodo .
ES. 0,27 = 27-0 = ……. ES. 1, 603 = 1603 – 160
99
900
a =
differenza tra il numero scritto senza la virgola numero scritto senza il periodo
b = tanti 9 quante sono le cifre del periodo, seguiti da tanti 0 quante sono le cifre
dell’antiperiodo
CASO PARTICOLARE:
0,9 = 9-0 = 1
9
3,9 non viene approssimato con 4 ma è direttamente 3, 9 è 4
OPPURE:
0,3 = 1: 3 = 1
3
0,3 • 3 = 1 • 3 = 1 ma 0,3 • 3 = 0,9
3
0,9 = 1