Nessun titolo diapositiva

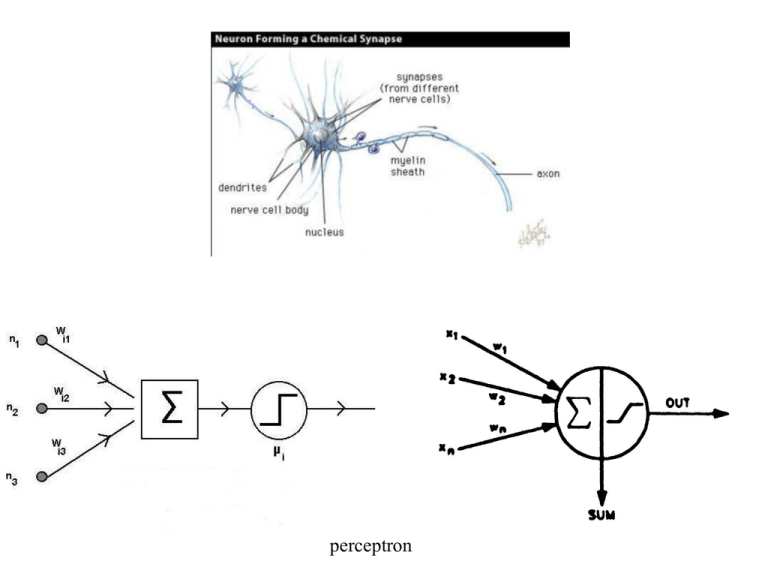
perceptron
1
f x 
1  e  x
e  x
f  x  
 f  x 1  f  x 
 x 2
1  e 
,3]
W [1
,[2
X2
W
[3,
W
[3,
W[2,3],[2,4]
o1 t1
o2 t2
o3 t3
1
2
k=1.....n
2],
[2,
3]
,4]
X3
4
3],
[2,
4]
X1
1
j=1.....m
2
3
3
n
SUMi, j   xk , j 1wk, j 1,i, j 
k 1
SUMi, j è la somma effettuata sul nodo i-esimo dello strato j
xk , j 1
n è il numero di nodi dello strato j-1
è l'output proveniente dal nodo k-esimo dello strato j-1, che è
anche uno degli input (pesati) del nodo i,j
wk , j 1,i, j  è il peso attribuito alla connessione tra i nodi k,j-1 e i,j
Addestramento della rete neurale
Un insieme rappresentativo di casi conosciuti è il set di addestramento.
Per un nodo di output i e per un membro p del set di addestramento, si ha un errore del segnale:
t p, i  o p, i
dove o è l'output registrato e t è l'output desiderato (target).
Si può valutare il comportamento complessivo della rete tramite la funzione di errore:
Ep   t p,i  op,i 
2
i
dove la Sè estesa a tutti i nodi dello strato di output.
Si variano i pesi
wk , j 1,i, j 
Il procedimento è iterativo.
delle connessioni al fine di ridurre la funzione d'errore.
Il procedimento più utilizzato è quello del gradiente (steepest descent):
wk , j 1,i , j  t  1  wk , j 1,i , j  t    p ,i , j  (t )o p ,i , j  t 
t indica il ciclo dell'iterazione
o p,i, j 
 è il passo, spesso compreso tra 0.001 e 1
è l'output che si ha dal nodo i dello strato j quando viene sottoposto alla rete il
membro p del set di addestramento.
 p ,i , j  (t )
viene calcolato diversamente a seconda che il nodo [i,j] sia un nodo di output o
faccia parte di uno strato intermedio:
1) nel caso si tratti di nodo di output (j è lo strato di output):
 p ,i , j  (t )  f SUM p ,i , j  t p ,i , j   o p ,i , j  
2) nel caso si tratti di nodo intermedio (j è uno strato intermedio):


 p ,i , j  (t )  f SUM p ,i , j    wi , j ,k , j 1 p ,k , j 1 


k
dove la S è estesa a tutti i nodi dello strato j+1
se si utilizza la funzione logistica:



 
f  SUM p,i, j   f SUM p,i, j  1  f SUM p,i, j 

,3]
W [1
,[2
X2
wi, j ,k , j 1
o2 t2
3],
[2,
4]
W
[3,
W[2,3],[2,4]
o1 t1
o3 t3
1
2
k=1.....n
2],
[2,
3]
,4]
X3
4
W
[3,
X1
1
j=1.....m
2
3
3
è il peso tra il nodo i dello strato j e il nodo k dello strato j+1
Esempio, per una connessione particolare, di modifica dei pesi riguardanti lo strato di output:
w1,3,2, 4  t  1  w1,3,2, 4  t   o p , 2 t  p ,2, 4  (t )
dove p è l'indice di un elemento dell'insieme di addestramento.
Modifica dei pesi riguardanti lo strato di output, in generale:
wl ,m 1,k ,m  t  1  wl ,m1,k ,m  t   o p ,k t  p ,k ,m  (t )
,3]
W [1
,[2
X2
o2 t2
3],
[2,
4]
W
[3,
W[2,3],[2,4]
o1 t1
o3 t3
1
2
k=1.....n
2],
[2,
3]
,4]
X3
4
W
[3,
X1
1
j=1.....m
2
3
3
 p ,2, 4  (t )  f SUM p ,2, 4  t p , 2  o p , 2 
 p ,k ,m  (t )  f SUM p ,k ,m  t p ,k  o p ,k 

1  f SUM


f SUM p, 2,4   f SUM p, 2,4  1 f SUM p, 2,4  
f SUM p, k ,m  f SUM p, k,m 
p, k,m 
1
,3]
W [1
,[2
X2

o2 t2
3],
[2,
4]
W
[3,
W[2,3],[2,4]
o1 t1
o3 t3
1
2
k=1.....n
2],
[2,
3]
,4]
X3
f SUM p,2,4 
4
W
[3,
X1
j=1.....m
2
3
3
 w

X
 1,3 ,2,4  1,3  
 f w2,3,2,4  X2,3   o p,2


w

X
 3,3,2,4  3,3 

 n

f SUM p ,k ,m    f   wl ,m1,k ,m  X l ,m1   o p ,k
 l 1

,3]
W [1
,[2
X2
o2 t2
3],
[2,
4]
W
[3,
W[2,3],[2,4]
o1 t1
o3 t3
1
2
k=1.....n
2],
[2,
3]
,4]
X3
4
W
[3,
X1
1
j=1.....m
2
3
3
Per la modifica dei pesi riguardanti lo strato interno a contatto con lo stato di output, cambia la
valutazione del :
 p ,2,3 (t )  f SUM p ,2,3 w2,3,1, 4  p ,1, 4  (t )  w2,3,2, 4  p ,2, 4  (t )  w2,3,3, 4 p ,3, 4  (t )
n

 p ,k ,m1 (t )  f SUM p ,k ,m1  wk ,m1,l ,m  p ,l ,m  (t )
 l 1

I  così calcolati saranno utilizzati per il calcolo delle variazioni dei pesi per lo strato m-2 e così
via in un processo di back propagation.
L'addestramento può essere fatto con un membro alla volta del set di addestramento, scelto a caso
(metodo stocastico), oppure contemporaneamente su tutto il set ad ogni ciclo (metodo standard,
più efficace). In tal caso  p ,i , j  t o p ,i , j  t  va sostituito con:
1 I
 I
 p ,i , j  t o p ,i , j  t     p ,i , j  t o p ,i , j  t 

I p 1
I p 1
dove la S è estesa a tutti i membri del set e I è il loro numero complessivo.
Si può partire con una scelta casuale dei valori iniziali dei pesi
wk , j 1,i, j 
Il procedimento di addestramento richiede spesso giorni di calcolo.
Il metodo del gradiente può avere come risultato un minimo locale e non il minimo assoluto.
Caratteristiche delle reti neurali
•Hanno una propria logica non connessa alla natura del problema, da cui consegue una vasta
applicabilità
•Sono in grado di interpolare e non di estrapolare rispetto al campo di valori delle variabili
presenti nel set di addestramento
•Hanno una struttura parallela che consente il calcolo su processori o computer in parallelo,
con una riduzione notevole del tempo di calcolo
•Mostrano tolleranza ai danneggiamenti, per cui un danno limitato a uno o pochi perceptron,
induce generalmente una riduzione nell’attendibilità e non una perdita completa di
operatività
Applicazioni delle reti neurali in campo chimico
•Interpretazione automatica di spettri complessi
•Previsione della struttura secondaria delle proteine globulari
•Valutazione di indicatori QSAR (quantitative structure-activity relationship)
•Predizione spettro NMR
•In generale per problemi multivariati e non lineari