Lezione 19_03

La scoperta dell’elettrone
Raggi catodici e esperienza di Thompson
Catodo
Schermo al fosforo
Anodo
Applicando un alto voltaggio a un gas rarefatto si osserva una regione illuminata sullo
schermo
Tesi: il catodo emette qualcosa che può viaggiare fino allo schermo: i raggi catodici
Esperienza di Thompson
Layout esperienza:
1. Tubo a raggi catodici
2. Armature di un condensatore per generare un campo elettrico
3. Spire per generare un campo magnetico
Le armature e le spire sono in grado di deflettere i raggi catodici (forza elettrostatica e
forza di Lorentz).
Analizzando la deflessione si osserva che i raggi catodi in realtà sono
particelle cariche negativamente
Forza di Lorentz:
v2
evB  m
r
Forze agenti sulla traiettoria b:
eE  evB
E
v
B
e
E
 2
m B r
e
v

m
Br
Esperienza di Millikan
Obiettivo: determinare la carica dell’elettrone
Un olio minerale viene nebulizzato su un condensatore. Le gocce elettricamente cariche
risentono del campo elettrico presente fra le armature.
Quando la goccia è sospesa nell’aria si ha:
qE  mg
Si osserva:
1. La carica è un multiplo intero di una carica e
2. La carica e è uguale a 1.61*10-19 C
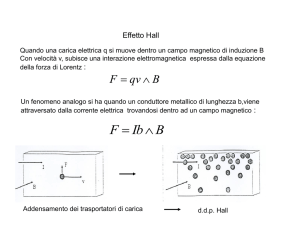
Effetto Hall
Un materiale conduttore percorso da corrente viene sottoposto a un campo magnetico.
La forza di Lorentz generata dal campo magnetico devia i portatori di carica.
Agli estremi del conduttore si genera un campo elettrico, detta tensione di Hall, pari a :
eEH  evd B
Se il conduttore è spesso d si ha:
VH  EH d  vd Bd
La polarità della tensione di Hall permette di identificare il segno dei
portatori di carica nel materiale
Consideriamo l’equazione della corrente:
I  nevd A
E’ possibile ricavare una grandezza RH, detta resistività di Hall
inversamente proporzionale al numero di portatori di carica
VH
Bd
RH 

I
neA
Spettrometro di massa
Strumento in grado di misurare la massa di una
particella/elemento/composto
E
v
B
Le particella ionizzata attraversa un selettore di velocità dal quale esce con velocità v
Successivamente entra in un’area in cui è presente un campo magnetico B’
m  qBB ' r / E
Misurando la curvatura della particella è possibile ricavarne la massa
Campi magnetici e fenomeni d’isteresi
Il campo magnetico generato da un solenoide è pari a:
B0  0 nI
Se all’interno del solenoide, al posto del vuoto, c’è un materiale
ferromagnetico
B  nI
Paramagnetismo e diamagnetismo
Nel caso del paramagnetismo un campo magnetico esterno orienta i dipoli magnetici
all’interno del materiale. Il campo magnetico risultante è:
B  0 (1   m ) H
Quando si va a “spegnere” il campo magnetico esterno i dipoli tornano ad essere orientati in
modo casuale
Il campo magnetico in un materiale diamagnetico presenta
la stessa formula del caso param. Ma il segno di Χm è
negativo: in pratica un materiale diamagnetico si oppone al
campo magnetico esterno.
Questo avviene perché le molecole non hanno un
momento di dipolo permanente.
Appendice: Millikan
L’equazione del moto della goccia è:
dove:
ma  m' g  6rv
4
m' g  (    a ) r 3 g
3
A regime la resistenza eguaglia la forza peso:
m' g 2(    a ) gr 2
v0 

6r
9
In presenza del campo elettrico:
ma  m' g  qE  6rv
La velocità di caduta risulta quindi:
qE
v1  v0 
6r
Da cui si ricava:
v1 
E
6r
q