Introduzione
alla
LOGICA MATEMATICA
Corso di Matematica Discreta.
Corso di laurea in Informatica.
Prof. Luigi Borzacchini
VII. Relazioni e funzioni
Le relazioni
• Il trattamento formale delle relazioni è una delle
novità principali della logica e della matematica
moderna.
• Nel formalismo di Frege la relazione è data
sintatticamente da un simbolo predicativo con due
o più argomenti: ama(Michele, Francesca) per
<Michele ama Francesca> o passa_per(r, A, B) per
<la retta r passa per i punti A e B>.
• Semanticamente una relazione R n-aria (cioè con n
argomenti) è data dall’insieme delle n-ple (a1, a2,…,
an) per le quali R(a1, a2,…, an) è soddisfatta. Se M è il
nostro universo, RMn
Consideriamo ad esempio l’insieme di tutti i numeri interi,
una relazione m-aria sarà quindi interpretata come un
sottoinsieme di m. Una relazione binaria su sarà un
sottoinsieme dell’insieme delle coppie: 2={(1,1), (1,2), (1,3),
…, (2,1), (2,2),…, (3,1),…, (n,m),…}.
Consideriamo per esempio la relazione binaria divisore(x,y),x|y
rappresentata dalle coppie
1
2 3 4 5 6 7 8
segnate con nella tabella.
1 ….
…. Nell’altro esempio abbiamo
2
3
…. la relazione ‘passa per’ tra due
4
5
6
Po Tevere Dora Adige Arno Aniene
….
…. Bari
…. Pisa
Roma
……………………………………………………….
Milano
insiemi diversi: città e
Torino
fiumi.
Firenze
I Grafi
• Un grafo è formato da un insieme di vertici V ed un
insieme di archi (formati da due vertici).
• Ma per arco possiamo intendere o una coppia
ordinata (a,b)V2 , come una strada a senso unico,
o una coppia non ordinata {a,b}, come una strada a
doppio senso (o un sentiero). Nel primo caso
parliamo di grafo diretto (o orientato), nel secondo
caso di grafo indiretto (o non orientato).
• Risulta chiaro quindi che nello studio delle relazioni
binarie risulta utile rappresentarle tramite grafi
diretti .
Per le relazioni binarie esiste quindi la rappresentazione
tramite un grafo diretto. Per gli esempi precedenti il grafo è:
(a sinistra per la relazione ‘divisore’ ignorando l’1 che è
divisore di tutti gli interi e le frecce di transitività, a destra per
la relazione ‘passa per’) Bari
Dora
2
4
6
9
3
5
8
10
7
Torino
Pisa
Firenze
Roma
Milano
Po
Arno
Adige
Tevere
Aniene
Un altro esempio già incontrato riguardava le relazioni di
‘inclusione’ tra insiemi o di ‘implicazione’ tra definizioni negli
alberi delle tassonomie o nell’insieme dei domini numerici.
Tutti gli esempi visti riguardavano relazioni binarie, le più
frequenti, ma in computer science si trovano relazioni con
più numerosi argomenti, come vedremo in seguito.
• Da una relazione binaria RXY si definisce la
relazione inversa R-1YX così definita (y,x)R-1
(x,y)R. Nella rappresentazione tramite grafo la
relazione inversa si ottiene semplicemente
invertendo le frecce (padre-1è figlio)
• Date due relazioni binarie RXY e SYZ, si può
definire la relazione composta RSXZ così definita
(x,z)RS y (x,y)R (y,z)S. Nella
rappresentazione tramite grafo la relazione
composta si ottiene da un cammino di due frecce.
Roma
Bergamo
Parigi
Cardiff
Milano
Glascow
Lazio
Ile de france
Scotland
Lombardia
Italia
Francia
Regno Unito
• Qual è la relazione inversa della relazione ‘divisore’?
Se divisore(4,20) 4|20 allora…… multiplo (20,4).
E quindi divisore-1 = multiplo. In termini insiemistici:
(x,y) multiplo (y,x) divisore. In termini logici:
multiplo (x,y) divisore (y,x) ovvero y|x.
Se R è la relazione fratello e S è la relazione padre,
allora RS è la relazione zio , in quanto x è lo zio di y se
esiste un z di cui x è fratello e che è il padre di y. In
termini insiemistici:
(x,y)RS z (x,z)R (z,y)S.
In termini logici:
zio(x,y) z fratello(x,z) padre(z,y)
Relazioni funzionali e funzioni
• Consideriamo la relazione nella_regione(x,y) da
interpretarsi come la frase <x è nella regione y>. La
sua interpretazione standard sarebbe: {(Firenze,
Toscana), (Torino, Piemonte), (Milano, Lombardia),
(Pisa, Toscana), (Roma, Lazio), (Bari, Puglia),…}.
• Essa ha una particolarità: ogni città può
appartenere al massimo ad una regione; una
relazione f(x,y) con tale proprietà si dice funzionale,
e da essa si può costruire una funzione y=f(x).
• Nel nostro esempio possiamo definire la funzione
regione: Toscana =regione(Firenze), Piemonte
=regione(Torino), Lombardia =regione(Milano), etc.
• L’insieme X su cui la funzione f è definita si dice
dominio, l’insieme Y dei suoi valori si dice
codominio, e si scrive f: XY. Se la funzione assume
un valore per ogni elemento del dominio si dice
totale, altrimenti si dice parziale.
• La funzione stato che ad ogni città associa lo stato
di appartenenza è totale in Europa, parziale negli
USA (in quanto Washington non appartiene a
nessuno stato).
• Una funzione f si dice ingettiva sse x y f(x)=f(y)
x=y, sul grafo cioè non esistono vertici del tipo
. Si dice surgettiva sse y x f(x)=y, cioè se ogni
vertice del codominio è raggiunto da una freccia.
Definizioni equivalenti della ingettività
• x y (f(x)=f(y) x=y) «se due elementi hanno
immagini coincidenti, allora coincidono»
• Dalla conversione: xy (xy f(x) f(y)) «elementi
diversi hanno immagini diverse» e trascrivendo l’ ,
otteniamo x y ( f(x)=f(y) x=y) , e dalle regole
che legano quantificatori e negazione la formula
diventa x y (f(x)=f(y) x y) «dato un qualsiasi
elemento non ne esiste un altro con la stessa
immagine» . Ovvero
x y ( f(x)=f(y) x y)
«non esistono due elementi distinti con la stessa
immagine»
• Una funzione si dice bigettiva se è ingettiva e
surgettiva, e si dice anche una corrispondenza
biunivoca o una corrispondenza 1-1.
• La composizione di una funzione f: XY con una
funzione g: YZ dà la funzione gf: XZ definita
come gf(x) = g(f(x)), che si ottiene come sequenza
delle due frecce x f gf g gf(x)
f(x)
• Se f è totale l’inversa f-1: YX, si ottiene -1
f
capovolgendo la direzione delle frecce f
• Se la funzione identica 1X: X X è definita x
1X(x)=x, allora f-1f = 1X, ff-1 = 1Y,
f-1(f(x))=x
f(x)
• Esempio: la relazione ‘a multiplo di b’ è la relazione
inversa della relazione ‘b è divisore di a’, ‘b divide a’.
Relazioni n-arie e funzioni (n-1)-arie
• Le relazioni binarie sono le più diffuse, ma si
trovano anche relazioni n-arie.
• Punto di partenza: il prodotto cartesiano
M1 M2 …Mn, l’insieme delle n-uple, (a1, a2,….
an), in cui a1 M1, a2 M2 ….., an Mn,
• Una relazione è un sottoinsieme di un prodotto
cartesiano: (a1, a2,…. an)R M1 M2 …Mn vuol
dire che gli elementi a1, a2,…. an sono in relazione R
• Se, fissati a1, a2,…. an-1 c’è un unico an per il quale
(a1, a2,…. an)R, allora si può definire la funzione fR
(n-1)-aria: fR (a1, a2,…. an-1 ) = an
• Definiamo ad esempio la relazione S ternaria su :
(a,b,c)S 3 sse aggiungendo b oggetti ad un
gruppo di a oggetti troviamo un gruppo di c oggetti,
ad esempio (3,6,9)S , scritto anche S(3,6,9), mentre
(4,3,8)S. Poiché fissati a e b è univocamente
determinato c, possiamo definire la funzione +:
2→ : a+b=c
• Se S è un alfabeto, S* è l’insieme delle parole su S:
(a,b,c)appendS*3 sse aggiungendo alla parola a la
parola b otteniamo la parola c, ad esempio (car, ta,
carta)append , scritto anche append(car, ta, carta),
mentre (ca, ne, gatto)append . Anche in questo
caso possiamo definire la funzione Append: S*2→
S*, append(car, ta)=carta
Logica e Matematica
• Nella matematica moderna, fondata sulla teoria degli
insiemi, sono molto importanti le distinzioni logiche tra
elementi (variabili e costanti), insiemi, funzioni, predicati
(sottoinsiemi e relazioni), proposizioni (formule).
•
è l’insieme dei numeri interi, i singoli numeri sono le
costanti; x, n, m, etc. denotano variabili che possono
assumere numeri come valori; funzioni sono le operazioni
che ad uno o più numeri associano un altro numero
(somma, prodotto, etc.); predicati sono proprietà vere su
uno o più numeri: nel primo caso individuano sottoinsiemi
(pariinsieme dei numeri pari), nel secondo relazioni (a è
minore di bl’insieme delle coppie (a,b) con a<b);
proposizioni (formule) esprimono fatti aritmetici, veri o falsi
Esempio: il minimo comune multiplo
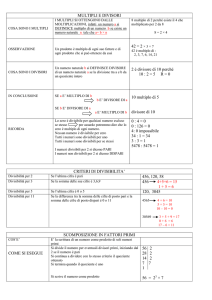
• Definiamo in la relazione binaria ‘a divide b’ a|b
m b=ma, e definiamo ‘c multiplo comune di a
e b’ a|c b|c, relazione ternaria su . Diciamo
‘n minimo comune multiplo di a e b’ il più piccolo dei
multipli comuni di a e b, cioè a|n b|n c (a|c
b|c) n c. E in tal caso si ha anche n|c
• Per le caratteristiche della relazione tale numero
esiste sempre ed è unico (un sottoinsieme non
vuoto di ha sempre un unico minimo), e quindi la
relazione ternaria ‘n minimo multiplo comune di a e
b’ può essere considerata come una funzione
binaria: n=mcm(a,b).
E proveremo anche che il mcm divide ogni altro comune
multiplo. Consideriamo mcm una relazione ternaria:
mcm(a,b,x) quando x è mcm di a e b.
Supponiamo per assurdo che i due numeri a e b abbiano due
distinti mcm. L’ipotesi assurda ha forma esistenziale: x y
mcm(a,b,x)mcm(a,b,y) (x=y)
e quindi iniziamo con una doppia sottoderivazione eliminazione: m ed n sono costanti nuove,
a|m b|m c (a|c b|c m|c )
a|n b|n d (a|d b|d n|d )
(m=n)
A questo punto entra in gioco l’intuizione: le variabili c e d
sono sostituibili nella -eliminazione con qualsiasi termine,
potrebbe essere utile farle coincidere con le costanti m e n
• possiamo sostituire a c il numero n e a d il numero
m, ottenendo
• a|m b|m (a|n b|n m|n )
a|n b|n (a|m b|m n|m)
• m|n
• n|m,
• x n=m x
In algebra studierete il
problema in e non in , e
• y m=n y
quindi la soluzione sarà ±1
• n=m x’
• m=n y’
• n= n y’ x’ e quindi y’ x’ = 1 da cui y’=x’=1 e
allora m=n. Ma (m=n)
e quindi
• Prendiamo a=6, b=15. I multipli di 6 sono: {6, 12,
18, 24, 30, 36, 42, 48, 54, 60 ...}, i multipli di 15
sono: {15, 30, 45, 60, 75, ...}, i loro multipli comuni
sono: {30, 60, 90, 120, 150, ...}, il loro minimo
comune multiplo è 30: 30=mcm(6,15), e gli altri
multipli comuni sono tutti e soli i multipli di 30.
•
3
6 12
24
48
• 2
18
36
45
•
5
15
30
60
• Analogo ragionamento per definire il ‘massimo
comun divisore’: i divisori di 6 sono: {1,2,3}, quelli di
15 sono: {1,3,5}, quelli comuni sono: {1,3} e quindi 3
= MCD(6,15).
Ancora la combinatoria
• La combinatoria conta le configurazioni simboliche,
ad esempio «quante parole distinte di lunghezza n
si possono costruire da una alfabeto di k segni?»
oppure «in quanti modi diversi si possono mettere
n palline distinte in k scatole?».
• Ad esempio se k=3 e n=2, le parole distinte sono
{aa, ab, ac, ba, bb, bc, ca, cb, cc}, mentre le
distribuzioni nelle scatole sono ab/Ø/Ø, a/b/Ø,
a/Ø/b, b/a/Ø, Ø/ab/Ø, Ø/a/b, b/Ø/a, Ø/b/a,
Ø/Ø/ab. In entrambi i casi abbiamo 9=32=kn
configurazioni: è un caso? In entrambi i casi sono le
funzioni da un n-insieme in un k-insieme.
• 1
I
• 2
II
•
III
•
aa
• ab/Ø/Ø
1
2
I
II
III
ab
a/b/Ø
1
2
I
II
III
ac
a/Ø/b
1
2
I
II
III
ba
b/a/Ø
1
2
I
II
III
bb
Ø/ab/Ø
1
2
I
II
III ……
bc
Ø/a/b
• Altro esempio: contiamo quante sono le
proposizioni non equivalenti (che hanno cioè
diversa tavola di verità) che si possono creare con n
proposizioni elementari.
• In primo luogo le diverse interpretazioni sono 2n , in
quanto ogni proposizione elementare può essere
vera o falsa. Poi per ogni interpretazione la
proposizione può essere vera o falsa, e quindi in
totale abbiamo 22 n diverse tavole di verità.
• Sia M un insieme di m elementi (distinti): |M|=m
• Le coppie ordinate di elementi di M sono:
X
• |M 2|= m 2
X
Quante sono le coppie ordinate di
X
X
elementi di M se non sono
X
ammesse ripetizioni? m 2 – m
X
E quante sono le coppie non
ordinate senza ripetizioni? (m 2 – m)/2
Possiamo generalizzare a Mn ? |M n|= m n
Le n-uple ordinate senza ripetizioni sono:
m (m-1) (m-2) … (m-n+1).
Ad esempio le terne ordinate su M = {a, b, c, d} sono
•
a
b
c
d
ab ac ad ba bc bd ca cb cd da db dc
abc abd acb acd adb adc bac bad bca bcd bda bdc cab cad cba cbd cda cdb dab dac dba dbc dca dcb
Se m=n otteniamo il numero degli ordinamenti
possibili di M: m! = m (m-1) (m-2) … 2 1
Ma una n-upla non ordinata (un sottoinsieme di n
elementi) può essere ordinata in n! modi diversi.
Ad esempio {a,c,d} corrisponde ai 6=3! ordinamenti
acd, adc, cad, cda, dac, dca. E quindi le n-uple su M
non ordinate (i sottoinsiemi di M di cardinalità n)
sono: (m (m-1) (m-2) … (m-n+1))/n! = (m-n)!
(m (m-1) (m-2) … (m-n+1))/ (m-n)! n!
(m(m-1)(m-2) …2 1)/(m-n)! n! = m!/(m-n)!n!
Il poker
𝑚
𝑛
scriviamo: m!/(m-n)!n! =
Quante ‘mani’ possibili?
52
5
Quanti poker? 13 48
Quanti poker di assi? 48
Quanti full di assi e k?
Full di assi? 24 12
numero di n-sottoinsiemi
da un m-insieme
4
3
4
2
= 24
Quanti full? 24 12 13
Quante doppia coppia di assi e k?
4
Quante doppia coppia? 2
13
Quanti colori a cuori? 5
4
2
4
2
4
2
44
44 13 12 / 2
Quante scale? 45 10