Diapositiva 1

ALCUNE PRECISAZIONI
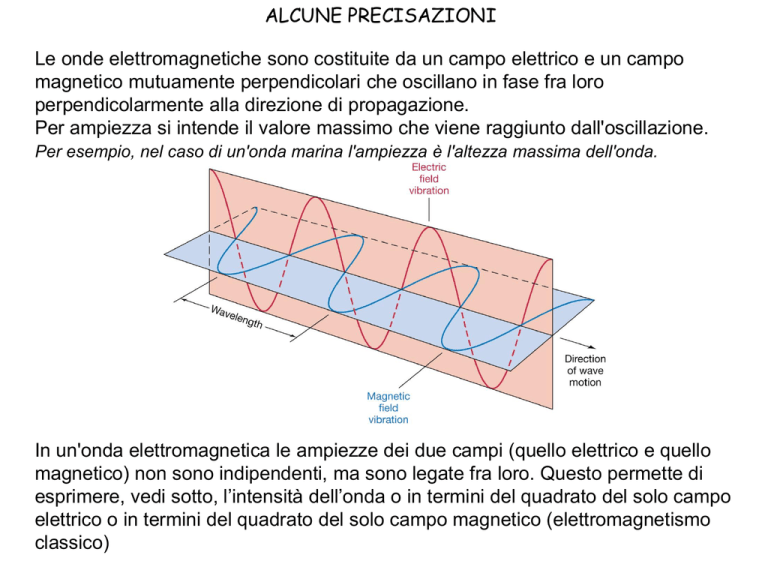
Le onde elettromagnetiche sono costituite da un campo elettrico e un campo
magnetico mutuamente perpendicolari che oscillano in fase fra loro
perpendicolarmente alla direzione di propagazione.
Per ampiezza si intende il valore massimo che viene raggiunto dall'oscillazione.
Per esempio, nel caso di un'onda marina l'ampiezza è l'altezza massima dell'onda.
In un'onda elettromagnetica le ampiezze dei due campi (quello elettrico e quello
magnetico) non sono indipendenti, ma sono legate fra loro. Questo permette di
esprimere, vedi sotto, l’intensità dell’onda o in termini del quadrato del solo campo
elettrico o in termini del quadrato del solo campo magnetico (elettromagnetismo
classico)
L'intensità di un'onda elettromagnetica è l'energia che passa attraverso un'area
unitaria nell'unità di tempo e si misura in watt/m2: è cioè l'energia che attraversa in
ogni secondo una superficie di un metro quadrato.
Si può dimostrare che l'intensità è proporzionale al prodotto delle ampiezze del
campo elettrico e del campo magnetico; poiché questi sono proporzionali tra loro,
in ultima analisi l'intensità è proporzionale al quadrato dell'ampiezza del campo
elettrico.
Polarizzazione di un'onda elettromagnetica
la propagazione delle onde elettromagnetiche avviene in direzione perpendicolare
alla direzione del campo elettrico e del campo magnetico (che sono componenti
dell’onda). Il piano individuato dalla direzione di propagazione e dal vettore
campo elettrico E si dice piano di polarizzazione. Se questo piano non cambia
al passare del tempo e mentre il campo si propaga, l’onda elettromagnetica è detta
polarizzata linearmente. Se invece il vettore campo elettrico E (e quindi anche il
vettore di campo magnetico H che è perpendicolare ad E) ruota al passare del
tempo e all’avanzare dell’onda (compiendo così una rotazione completa in un
periodo T) si dice che l’onda ha una polarizzazione ellittica; se, poi, in particolare, il
vettore campo elettrico e il vettore campo magnetico ruotano mantenendo
un’ampiezza costante, si parla di polarizzazione circolare.
Simulazioni interattive, per esempio, agli indirizzi:
http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=35
http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=284.0
Intensità specifica della radiazione
Si riferisce alla energia irraggiata dalla
superficie unitaria ad unità di tempo (ad
unità di angolo solido) ad unità di
lunghezza d’onda.
Densità specifica della radiazione
Si riferisce alla energia elettromagnetica
ad unità di volume e di lunghezza d’onda
all’interno della cavità radiante.
Sono collegate tra loro e spesso si parla dell’una o dell’altra
indifferentemente o si passa dall’una all’altra senza avviso.
Facciamo chiarezza sulle unità di misura delle due grandezze e sul loro collegamento
I   B
J
 I   2
m  s   m  ( srad )
J
I

  3
m  s  ( srad )

   
J
m3   m
   
J
m4
Intensità specifica della radiazione
Densità specifica della radiazione
Si riferisce alla energia irraggiata dalla
superficie unitaria ad unità di tempo (ad
unità di angolo solido) ad unità di
frequenza.
Si riferisce alla energia elettromagnetica
ad unità di volume e di frequenza
all’interno della cavità radiante.
Sono collegate tra loro e spesso si parla dell’una o dell’altra
indifferentemente o si passa dall’una all’altra senza avviso.
Facciamo chiarezza sulle unità di misura delle due grandezze e sul loro collegamento

I  B
Per collegare le unità di misura di B , B è necessario tener conto
che ad aver significato fisico, essere misurabili, non sono le funzioni
scritte ma le:
I  d   B d 
I d  B d
Che rappresentano l’energia emessa dall’unità di superficie nell’unità di tempo e di
angolo solido tra  e   d 
e
rispettivamente
 e   d
B
Allora per collegare, ad esempio, la
con la
B
si ha:
d
B d   B d  B  B
d
ma è

da cui infine
c


B  B
d 
c

2
c

2
d
(trascurando un segno negativo
privo di significato fisico)
d
che spiegano le due espressioni:
2πhc
B  λ,T  
λ5
-3
erg cm s
-1
1
2
e
hc
kλT
1
W
m3
2πh 3
B  ,T  
c2
erg cm
-2
1
e
hν
kT
1
W
m 2 s -1
e che,
B  I   B d    B d   I  d    I d



quindi, poiché si ha:
 I    B 
J
J
W


m2  s  ( srad ) m2  s  ( srad ) m2  ( srad )
risulta:
 B  
W
J

m2  s 1 ( srad ) m2  ( srad )

Passiamo ora al legame tra le densità specifiche di radiazione e le intensità specifiche.
Tenendo conto che la radiazione emessa dalla superficie è in tutte le direzioni si
ricava che
c
I 
4