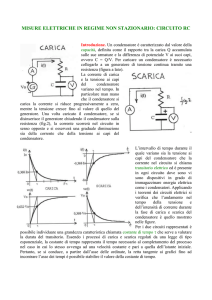
I condensatori
I condensatori sono componenti elettronici che hanno la capacità di immagazzinare (caricare)
energia elettrica.
Essi si caricano allo stesso valore della sorgente di alimentazione; una volta raggiunta la carica
essa viene mantenuta nel tempo anche se il condensatore non è più collegato al generatore e
fino a quando i terminali non vengono collegati ad una resistenza o posti in corto-circuito.
+
_
C
+
+A
_
_
B
E
I condensatori sono essenzialmente costituiti da due armature metalliche isolate tra di loro.
La capacità è direttamente proporzionale alla superficie delle armature ed inversamente
proporzionale alla loro distanza, e dipende in modo direttamente proporzionale, dal valore
della costante dielettrica dell'isolante usato
L'isolante posto tra le armature viene chiamato "dielettrico" e può essere liquido, solido o
gassoso.
L'unità di misura della capacità è il Farad (F) che è un valore molto grande e quindi si
utilizzano quasi sempre i sottomultipli.
E' stato già detto che i condensatori sono componenti che hanno la capacità di "caricarsi" e
che si caricano allo stesso potenziale della tensione di alimentazione.
Il principio per cui ciò avviene è il seguente:
Inizialmente, a condensatore scarico, le armature sono elettricamente neutre,
avendosi, su ognuna di esse, lo stesso numero di elettroni e di protoni
Quando il condensatore viene collegato ad un generatore di tensione continua, avviene
che il polo positivo del generatore attira elettroni dall'armatura a cui è collegato,
mentre l'altra armatura attira elettroni dal polo negativo del generatore.
La carica del condensatore, intesa come d.d.p. tra le armature, aumenta man mano che
si verifica questo movimento di elettroni. Il numero di elettroni che circolano nel
circuito è inizialmente massimo per poi decrescere man mano che il condensatore si
carica.
Una volta che il condensatore si è caricato (allo stesso valore di tensione del
generatore), si avrà che sulla armatura A ci sarà mancanza di elettroni e quindi una
predominanza di cariche positive e quindi sarà a potenziale positivo, mentre
sull'armatura B ci sarà predominanza di elettroni e quindi sarà a potenziale negativo.
La tensione (la carica) viene mantenuta anche se si scollega il condensatore
dall'alimentatore (nell'ipotesi di condensatore ideale, senza perdite).
Si dimostra che la quantità di carica accumulata su una delle due armature è proporzionale
alla tensione fra le due armature:
Q = CV
dove C è una costante di proporzionalità, che si misura in Farad, dipende dalle dimensioni e
dalle caratteristiche chimiche del dielettrico utilizzato. Cerchiamo, adesso, una relazione tra
tensione e corrente. Supponiamo che la tensione passi da un valore V1 a un valore V2 , allora
possiamo scrivere:
Q1 = CV1 e Q2 = CV2. Sottraendo membro a membro otteniamo Q2 – Q1 = CV2 – CV1.
Se poniamo Q2 – Q1 = ΔQ e V2 – V1 = ΔV allora avremo ΔQ = C ΔV (1).
Quest’ultimo è un legame alle differenze finite, cioè tra le variazioni di tensione ΔV e le
variazioni di carica ΔQ. Se Q1 è misurata nell’istante di tempo t1 e Q2 nell’instante t2, sappiamo
che, per definizione, la corrente è la carica che fluisce in un secondo, in Δt secondi fluirà una
quantità di carica pari a: ΔQ = Im Δt (2). Sostituendo al valore di ΔQ nella (2) con il valore di
ΔQ nella (1) si ottiene: C ΔV = Im Δt da cui :
Si noti come questa relazione non esprime un legame assoluto tra corrente e tensione, ma ci
dice che la quantità media di corrente che circola nel condensatore è uguale al rapporto tra la
differenza di tensione ΔV e Δt, che possiamo chiamare rapporto incrementale, per una
costante di proporzionalità C. Se vogliamo conoscere il valore istantaneo della corrente che
circola nel condensatore dovremmo considerare un intervallo di tempo Δt infinitesimamente
piccolo (Δt → 0). Avremo:
Induttore
L'induttore è un componente elettrico che genera un campo magnetico al passaggio di
corrente elettrica (continua o alternata od impulsiva). Nella teoria dei circuiti l'induttore è un
componente ideale (la cui grandezza fisica è l'induttanza) in cui tutta l'energia elettrica
assorbita è immagazzinata nel campo magnetico prodotto. L’equazione caratteristica
dell’induttore è duale rispetto a quella del condensatore. basta scambiare tra loro i termini di
tensione e corrente e sostituire al posto della capacità C l’induttanza L:
Il simbolo dell’induttore è il seguente:
Circuito RC
D
B
R
+
C
_
E
A
Ramo (o arco o lato): singolo percorso circuitale (tra due nodi)
Nodo: punto in cui convergono almeno due rami
Maglia: insieme di due o più rami che formano un cammino chiuso
È un circuito di fondamentale importanza, in quanto racchiude tutti i concetti di base.
Vogliamo studiare l’andamento della tensione di uscita, coincidente con la tensione Vc(t) del
condensatore, per un ingresso di tensione a gradino, cioè che sale istantaneamente da 0 al
valore massimo costante E.
Sulle maglie del circuito è valida la legge di Kirchhoff alle maglie , che prevede che la somma
delle tensioni sui rami di una maglia (percorso chiuso attraverso i rami di un circuito) deve
essere zero, oppure, detto in altri termini: in ogni maglia la somma algebrica degli incrementi
di potenziale (E) è uguale alla somma delle diminuzioni di potenziale ( VR(t), VC(t)).
-Vc(t) -VR(t) + E = 0 da cui E = Vc(t) +VR(t)
(3)
Notiamo che la tensione di ramo è positiva se la corrente di maglia attraversa il generatore dal
polo negativo al polo positivo, altrimenti è negativa
A questo punto dobbiamo prendere in considerazione legge di Kirchhoff ai nodi che prevede
che la soma algebrica delle correnti affluenti ad un certo nodo è zero, cioè la somma delle
correnti che entrano e delle correnti che escono da quel nodo deve valere zero. Questa
implica, ad esempio, che al nodo B debba risultare:
iR(t) - iC(t) = 0 da cui iR(t) = iC(t)
Sfruttando la legge di Ohm: (V=R I) VR(t) = R iR(t) = R iC(t)
Ricordando l’equazione caratteristica del condensatore, cioè,
possiamo scrivere:
che sostituita alla (3) ci consente di scrivere un’equazione in una sola incognita Vc(t):
la quantità costante RC la indichiamo con il simbolo τ otteniamo l’equazione alle differenze
per il circuito RC:
Scriviamo ora:
da cui sostituendo e isolando il termine
metodo numerico:
otteniamo l’equazione risolvibile con
Questa formula ci consente il calcolo ricorsivo dei valori di tensione ai capi del condensatore.
Partendo dal valore iniziale Vc(0) è possibile calcolare, applicando ricorsivamente la formula,
i valori successivi di tensione. Questo metodo ricorsivo è approssimato ed i risultati sono
tanto più vicini ai valori reali, quanto minore è l’intervallo
, detto passo di simulazione.
Circuito RLC
R
L
+
C
_
E
E’ un circuito in cui si introduce un elemento nuovo rispetto al circuito RC, che è la presenza di
oscillazioni.. Per determinare l’equazione risolutiva impostiamo l’equazione alla maglia:
E = Vc(t) + VR(t) + VL(t)
(4)
In questo caso conviene avere due equazioni, una rispetto a Vc(t) e l’altra rispetto a i(t).
Sostituendo nella (4) alla VL(t) l’equazione caratteristica dell’induttore:
Isoliamo i termini alle differenze relativi a Vc(t) e
da cui
Che rappresenta l’equazione numerica che esprime i valori futuri delle due incognite in
funzione di quelli presenti.