La corrente elettrica

Prof. Antonello Tinti
LA CORRENTE ELETTRICA
1
La corrente elettrica
Si chiama CORRENTE ELETTRICA un moto ordinato di cariche
elettriche prodotto dall’azione di un CAMPO ELETTRICO
Possiamo anche dire che la corrente elettrica è un passaggio di
cariche elettriche in un conduttore determinata da una d.d.p. che
viene ricostruita continuamente da un’apposito dispositivo chiamato
GENERATORE.
ΔV
+
Il moto delle cariche è simile al moto
di un liquido
+
+
+
+
-
Le cariche si muovono dal
potenziale maggiore al potenziale
minore
2
La definizione di intensità di
corrente elettrica
+
-
+
+
-
S
+
- +
-
-
E
Si chiama intensità i di corrente elettrica il rapporto tra la quantità
di carica ΔQ che attraversa una sezione S del conduttore e
l’intervallo di tempo Δt impiegato ad attraversarlo.
Q
i
t
3
L’unità di misura è l’Ampere
1 Ampere è l’intensità di corrente che
trasporta la carica di 1 Coulomb in 1 secondo
1C
1A 
1s
Verso positivo della corrente quello in cui si muovono le cariche positive
E
Per convenzione il verso
della corrente è quello delle
cariche positive
Verso negativo della corrente quello in cui si muovono le cariche negative.
4
L’intensità di corrente è una GRANDEZZA UNITARIA, simile alla
portata di un fiume o al traffico giornaliero medio
5
Una corrente elettrica si dice CONTINUA
quando la sua intensità non cambia nel
tempo
La corrente elettrica domestica non è
continua ma ALTERNATA perché le cariche
vanno avanti e indietro 50 volte al secondo
(frequenza di 50 Hz).
6
Q
i
t
Q  i  t
In una corrente continua (i=costante), la carica che attraversa una sezione del
filo e il tempo trascorso sono direttamente proporzionali.
pompa
Si chiama GENERATORE DI CORRENTE
CONTINUA un dispositivo elettrico capace
di mantenere ai suoi capi una d.d.p.
costante, per un intervallo di tempo
indeterminato e qualunque sia la corrente
da cui è attraversato
V
- +
7
La corrente nei conduttori metallici
Traiettoria in assenza di campo
elettrico
Reticolo cristallino di un metallo e gli
elettroni di conduzione
La velocità di deriva vd
Traiettoria in presenza di campo elettrico
8
Campo elettrico
9
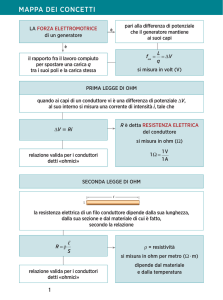
La forza elettromotrice
Un generatore di tensione ha la funzione di mantenere ai suoi capi una
d.d.p. costante. Per fare ciò deve compiere al suo interno un lavoro
per spostare le cariche elettriche in verso opposto a quello in cui si
sposterebbero spontaneamente.
La forza elettromotrice (fem) di un generatore è il
LAVORO per unità di carica che esso compie per
spostare le cariche al suo interno
L
fem 
Q
Joule
 Volt
Coulomb
10
In questo spazio una
forza muove le cariche
in modo da mantenere
costante la d.d.p.
11
4.5 V
1.5 V
12 V
12
La densità di corrente j
L’intensità di corrente i è una caratteristica macroscopica di ogni singolo
conduttore
La densità di corrente j è invece una caratteristica microscopica del
conduttore
È una grandezza vettoriale, ed è una caratteristica locale di ogni punto
interno al conduttore
E
+
+
+
+
+
A
-
Direzione e verso della forza a cui sarebbe soggetta
una carica positiva in quel punto.
13
Possiamo calcolare la velocità di deriva vd degli elettroni di conduzione a
partire dalla densità di corrente
n  A L
Numero n di elettroni di conduzione in un tratto di cavo L
n rappresenta il numero degli elettroni di conduzione per unità di volume
A∙L rappresenta il volume del tratto di cavo
q  nAL e
i
vd 
nAe
L
t
vd
j
vd 
ne
q nAL   e
i 
 nAevd
L
t
vd
La velocità vd avrà la
stessa direzione di j ma
verso opposto
j  nevd
14
Resistenza e resistività
RAME
LEGNO
∆V
∆V
Se applichiamo la stessa d.d.p. abbiamo correnti diverse
PERCHE’ ?
Dipende dalla RESISTENZA ELETTRICA del conduttore
15
V
R
i
1Volt
R 
 1Ohm  1 
1Ampere
Un conduttore che in un circuito ha la funzione di fornire una data resistenza si
chiama RESISTORE
16
17
La RESISITIVITA’  è un’altra grandezza fisica legata alla resistenza.
Essa è una caratteristica del particolare MATERIALE costituente il conduttore
E

j
V
Vm
m
   A   m
A
2
m
18
19
Dalla resistività alla resistenza
E
+
V
E
L
+
+
i
j
A
Per conduttori omogenei, isotropi
con sezione ortogonale uniforme
soggetti ad un campo uniforme
+
A
+
-
V
E L VA
A
  
 R
i
j
iL
L
A
L
R 
A
20
La prima legge di Ohm
V
- +
i
V
V
- + - +
2i
V
V
- + - + V
- +
3i
L’intensità di corrente dipende dalle caratteristiche fisiche del
conduttore e dalla d.d.p. del generatore
V
R
i
L’intensità di corrente elettrica che scorre in un
conduttore è direttamente proporzionale alla d.d.p.
applicata ai suoi capi
21
V
I
R
La seconda legge di Ohm
La resistenza di un filo conduttore è direttamente
proporzionale alla sua lunghezza ed inversamente
proporzionale alla sua sezione
L
R 
A
23
Possiamo avere più utilizzatori, ciascuno con la sua resistenza, collegati in:
1. Tutti in serie.
2. Tutti in parallelo.
3. Parte in serie e parte in parallelo.
24
Più utilizzatori si dicono collegati in SERIE, quando la
corrente elettrica uscente da ciascuno di essi, ha la
stessa intensità di quella entrante nel successivo.
La d.d.p. ai capi del generatore deve essere uguale
alla somma delle d.d.p. ai capi di ciascun
utilizzatore.
V1  iR1
V2  iR2
V1  V2  V
Per la 1° legge di Ohm
R1  R2  Re
iR1  iR2  iRe
iR1  R2   iRe
Resistenza equivalente
Più utilizzatori sono “visti” dal generatore come un
unico utilizzatore avente come resistenza la somma
delle resistenze dei singoli utilizzatori
V
V  iRe i 
Re
25
Più utilizzatori sono disposti in parallelo quando ai
loro capi esiste la stessa d.d.p.
L’intensità di corrente erogata dal generatore è la
somma delle intensità di corrente assorbite da
ciascun utilizzatore.
i1  i2  i
V
i1 
R1
V
i2 
R2
1
1
1
 
Re R1 R2
Per la 1° legge di Ohm
1
V V
1 
i1  i2 

 V   
R1
R2
 R1 R2 
V
i
Re
L’inverso della resistenza si
chiama CONDUTTANZA
Più utilizzatori in parallelo sono “visti” dal generatore come un unico
utilizzatore avente come CONDUTTANZA la somma delle conduttanze dei
singoli utilizzatori
26
La potenza elettrica
L  V  q
U  V  i  t
Quando un generatore G trasferisce una carica
elettrica q attraverso una certa d.d.p. compie un
lavoro L
Tale lavoro si identifica con l’energia potenziale U
fornita dal generatore G per far circolare la corrente
i per un tempo t
Questa energia U è ottenuta a spese di altra energia (meccanica, chimica, …).
E a sua volta questa energia viene trasformata nel circuito in altre forme
(meccanica, chimica,…)
Quando il circuito è Ohmico tutta l’energia
elettrica assorbita viene integralmente
trasformata in calore
U  R i2 t
27
U  V  i  t
Dividendo ambo i membri per t
U V  i  t

t
t
P  V  i
La potenza elettrica rappresenta l’energia termica per unità
di tempo prodotta dal passaggio della corrente nel
conduttore
Nel caso dei conduttori Ohmici
P  R i
2
V
P
R
2
28
Unità di misura
P  Volt  Ampere
Joule Coulomb
Joule
P


 Watt
Coulomb secondo secondo
Quando ci si riferisci ai consumi di energia elettrica si usa il chilowattora
È l’energia trasformata in 1 ora in un
circuito che assorbe la potenza di 1kW
1kWh  1000W  3600 sec  3.6 10 j
6
29
Effetto Joule
Nei conduttori puramente Ohmici, l’energia elettrica U si trasforma
totalmente in calore
U  R i2 t
calore
Se U è espresso in Joule e Q in calorie
J
R  i  t  4.18
Q
cal
2
Legge di Joule
J
U  4.18
Q
cal
In qualunque conduttore percorso da
corrente è sempre presente l’effetto Joule.
Il calore prodotto è direttamente
proporzionale alla resistenza R
30
La resistenza interna di un generatore di fem
+
1,5V
Un generatore IDEALE è in grado di
fornire qualsiasi intensità di corrente
Un generatore REALE invece ha un limite alla
quantità di corrente che può erogare
-
Sia R=0.01  la resistenza di un corto filo di
rame
iddp fem
1.5V

 150 A
0.01
2
P  R  iddp
 fem  0.01  150 A  225W
2
Questa corrente elettrica dissiperebbe una potenza che lo vaporizzerebbe
31
Ma questo sappiamo che non accade, quindi la ddp ai capi della pila
non è 1,5V ma è inferiore.
Diciamo che 1,5V è la ddp della pila quando non eroga corrente.
Quando la pila eroga corrente la ddp è sicuramente inferiore
+
Rinterna
La resistenza interna è una caratteristica
intrinseca del generatore: più è grande,
meno corrente il generatore riesce ad
erogare
-
32
Calcoliamo la caduta di potenziale
+
Ri
i
V
∆V = fem
fem
-
fem
fem

Req Ri  Rc
Ri
Vint  Ri  i  fem
Ri  Rc
i
V  fem  Vint  fem  fem
+
Ri
-
V
Rc
∆V < fem
fem
Ri
Ri  Rc
i
V  fem
Rc
Ri  Rc
i
33
Se la Rc è molto grande rispetto alla Ri allora Ri + Rc  Rc e l’intensità di corrente
è molto piccola e quindi il generatore si comporta quasi come un generatore
ideale.
V  fem
Rc
Ri  Rc
V  fem
Rc
 fem
Rc
Quando il circuito è aperto non passa corrente e allora la
ddp è uguale alla fem
La forza elettromotrice fem
è la ddp di un generatore a
circuito aperto
Se la Rc è molto piccola rispetto alla Ri allora l’intensità di corrente dipende da
quest’ultima e il generatore funziona male
34