Lezione-14

Autronica
LEZIONE N° 14
ALGEBRA BOOLEANA
•
•
•
•
•
•
•
•
•
•
•
•
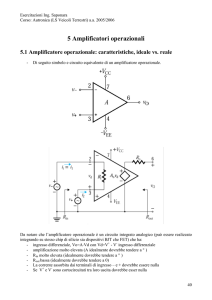
Postulati
Principio di dualità
Teoremi fondamentali
insieme funzionalmente completo NAND e NOR
Funzione XOR
Reti logiche combinatorie e sequenziali
Simboli
Concetto di ciclo
Concetto di minimizzazione (funzione costo)
Realizzazioni diverse della stessa funzione
Half Adder e Full Adder
Sommatori di due word di n bit
AUTRONICA
14.1
Richiami
•
•
•
•
•
•
Insieme di elementi
Variabili, costanti
Insieme di operazioni
Insieme di postulati
Espressioni algebriche
Tabella di verità
AUTRONICA
14.2
Postulati di HUNTINGTON
Algebra Booleana
1a
2a
Almeno due elementi distinti
Somma logica ( )
1b
Prodotto logico ()
x0 x
Elementi Identità
2b
x 1  x
Proprietà Commutativ a
3a
x y  yx
3b
x y  y x
Propèrietà Distributi va
4a x   y  z    x  y    x  z  4b x   y  z    x  y   x  z 
Complement azione
5a
x  x 1
5b
AUTRONICA
x x  0
14.3
Osservazioni
• Alcune proprietà dell’algebra booleana sono
vere anche nell’algebra normalmente usata:
– Proprietà commutativa
– Proprietà distributiva del prodotto logico
• Altre proprietà non sono vere :
– Proprietà distributiva della somma logica
• L’operazione complemento logico esiste solo
nell’algebra booleana
• La sottrazione e la divisione non esistono
nell’algebra booleana
AUTRONICA
14.4
Principio di DUALITÀ
• Da un’osservazione dei postulati precedenti si
osserva che quelli “b” si ottengono da “a”
– Scambiando i due operatori binari fra loro,
(+) con () e () con (+)
– Scambiando fra loro i due elementi identità,
1 con 0 e 0 con 1
AUTRONICA
14.5
TEOREMI FONDAMENTALI
• Tecniche di dimostrazione dei teoremi
– Impiego dei postulati fondamentali
– Uso di teoremi precedentemente dimostrati
– Dimostrazione per assurdo
• (si ipotizza verificata l’ipotesi opposta a quella
desiderata e si conclude che non è possibile che
sia vera)
– Dimostrazione per induzione
• (se una ipotesi è vera per k variabili e per k+1
variabili allora è vera per qualunque n)
AUTRONICA
14.6
Osservazione
• La tabella di verità consente di provare la
veridicità di una relazione logica, poiché
verifica se la relazione è vera per TUTTE le
possibili combinazioni dei valori delle variabili
• Tale metodo prende il nome di
• Metodo dell’INDUZIONE PERFETTE
AUTRONICA
14.7
TEOREMI
•
1a
x 1  1
2a
 x  x
x0  0
1b
3a
4a
xx  x
x  xy  x
3b
4b
x x  x
x x  y   x
5a
x  xy  x  y
5b
x x  y  xy
6a x   y  z    x  y   z  x  y  z
7a xy  xz  yz  xy  xz
8a
x  y   x  y
6b


xyz    xyz  xyz



7b  x  y  x  z  y  z    x  y  x  z
8b
AUTRONICA
x  y   x  y
14.8

Esempio di dimostrazione
• Teorema di De Morgan (8a e 8b)
8a x  y   x  y
8b x  y   x  y
x
y
x
y
x+y
(x + y)
x·y
0
0
1
1
0
1
1
0
1
1
0
1
0
0
1
0
0
1
1
0
0
1
1
0
0
1
0
0
AUTRONICA
c.v.d.
14.9
Osservazioni
1. I teoremi di destra si possono ottenere da
quelli di sinistra scambiando OR con AND e
“0” con “1”
2. Principio di dualità
3. Molti dei teoremi visti sono veri anche
nell’algebra che conosciamo
4. Particolarmente significativi sono i teoremi di
De Morgan e la proprietà distributiva
5. Molti teoremi, in particolare quelli di De
Morgan, sono veri anche per “n” variabili
AUTRONICA
14.10
Esempio 1
• Semplificare la seguente espressione:
x  z   x  z  y  z 
• In base ai teoremi visti si ha:
x  z   x  z  y  z   x  z  z  y  z 
  x  0   y  z 

 x y  z
x0  0

P 4b
P 5b
P 2a
1a
x 1  1
3a
4a
xx  x
x  xy  x
3b
4b
x x  x
x x  y   x
1a Somma logica ()
1b
Prodotto logico ()
2a
x0 x
2b
x 1  x
3a
x y  yx
3b
x y  y x
4a x   y  z    x  y   x  z  4b x   y  z    x  y    x  z 
5a
x  xy  x  y
5b
x x  y  xy
5a
1b
2a
6a x   y  z   x  y  z
 x  x
6b


xyz    xyz  xyz



7a xy  xz  yz  xy  xz 7b x  y  x  z  y  z    x  y  x  z
8a
x  y   x  y
8b
x  y   x  y
x  x 1
5b
x x  0

AUTRONICA
14.11
Esempio 1’

• Per altra via; posto:
• si ha:
T  xz

x  z   x  z  y  z   x  z   T  y  z 
 T  x  T  z   y  z 


 
 
 xx  xz  z x  z z  y  z
 x  xz  z x  z z  y  z
 x  0  y  z
 x y  z

1a
x 1  1
3a
4a
xx  x
x  xy  x
3b
4b
x x  x
x x  y   x
5a
x  xy  x  y
5b
x x  y  xy
6a x   y  z   x  y  z
 x  x
6b


xyz    xyz  xyz

1a Somma logica ()
1b
Prodotto logico ()
2a
x0 x
2b
x 1  x
3a
x y  yx
3b
x y  y x
4a x   y  z    x  y   x  z  4b x   y  z    x  y    x  z 


7a xy  xz  yz  xy  xz 7b x  y  x  z  y  z    x  y  x  z
8a
x  y   x  y
8b

x0  0
1b
2a


P 4b
P 4a
P 3b
x  y   x  y

5a
x  x 1
AUTRONICA
5b
x x  0
14.12
Premessa 1
• Osservazioni
– le funzioni AND, OR e NOT costituiscono un insieme
funzionalmente completo di operatori logici
– In base al teorema di De Morgan si ha:
 
x  y  x y
– ovvero la funzione OR si può realizzare con le
funzioni AND e NOT quindi:
– le funzioni AND e NOT costituiscono un insieme
funzionalmente completo di operatori logici
AUTRONICA
14.13
Premessa 2
• Osservazioni
– Sempre in base al teorema di De Morgan si ha:

x y  x y

– ovvero la funzione AND si può realizzare con le
funzioni OR e NOT quindi
– le funzioni OR e NOT costituiscono un insieme
funzionalmente completo di operatori logici
– le funzioni OR e AND non costituiscono un insieme
funzionalmente completo di operatori logici perché
non è possibile realizzare la funzione NOT
AUTRONICA
14.14
Definizione
• Le funzioni NAND e NOR sono definite dalle
seguenti tabelle di verità
x
0
0
1
1
y
0
1
0
1
u
1
1
1
0
x
0
0
1
1
NAND u   x  y 
y
0
1
0
1
u
1
0
0
0
NOR u   x  y 
AUTRONICA
14.15
Osservazioni
•
•
NAND e NOR sono contrazioni di
NOT-AND e NOT-OR
la funzione NAND costituisce un insieme
funzionalmente completo di operatori logici
 x  x  x
•
x  y   x  y
la funzione NOR costituisce un insieme
funzionalmente completo di operatori logici
 x  x   x x  y   x  y
AUTRONICA
14.16
Funzioni “complesse” 1
• L’operatore “XOR”, OR ESCLUSIVO è:
• Definizione
x y
x
0
0
1
1
y
0
1
0
1
u
0
1
1
0


x  y  x  y  x  y  x  y   x  y  x  y   x  y 
AUTRONICA
14.17
Funzioni “complesse” 2
• L’operatore “XNOR”, NOR ESCLUSIVO è:
• Definizione
x y
x
0
0
y
0
1
u
1
0
1
1
0
1
0
1


x y  x y  x y  x  y  x  y
AUTRONICA

14.18
Reti Logiche
• Sistema elettronico che ha in ingresso segnali
digitali e fornisce in uscita segnali digitali
secondo leggi descrivibili con l’algebra
Booleana
a
b
n



R. L.



x
y
w
• R.L. è unidirezionale
AUTRONICA
14.19
Tipi di reti
• Reti COMBINATORIE
• In qualunque istante le uscite sono funzione del
valore che gli ingressi hanno in quell’istante
• Il comportamento (uscite in funzione degli
ingressi) è descritto da una tabella
• Reti SEQUENZIALI
• In un determinato istante le uscite sono funzione
del valore che gli ingressi hanno in quell’istante e
i valori che hanno assunto precedentemente
• La descrizione è più complessa
• Stati Interni
• Reti dotate di MEMORIA
AUTRONICA
14.20
Simboli
• Rete Logica =>scomponibile in blocchi
• Blocchi base = simboli degli operatori
elementari
• Rappresentazione delle funzioni logiche
mediante schemi
• RAPPRESENTAZIONE SCHEMATICA
AUTRONICA
14.21
Porte logiche
• Rappresentazione circuitale delle funzioni
logiche
– AND
Y  X1  X 2  X 3
X1
X2
X3
Y
Y  X1  X 2
X1
X2
Y
– OR
– NOT
YX
X
AUTRONICA
Y
14.22
Esempio
• Schema simbolico della funzione
U  f  X 1 , X 2 ,, X n    X 1  X 2    X 1  X 3 
– RETE LOGICA
X1
X2
Xn
RETE
LOGICA
U = f(X1, X2,…., Xn)
x1  x2
X
1
X2
U
X
3
x1  x 3
x3
AUTRONICA
14.23
Altre porte logiche
• NAND
X Z Y
0 0 1
0 1 1
Y  X Z
X
Z
Y
Y  X Z
X
Z
Y
1 0 1
1 1 0
• NOR
X Z Y
0 0 1
0 1 0
1 0 0
1 1 0
AUTRONICA
14.24
Proprietà della porta NAND (NOR)
• Utilizzando solamente porte NAND (NOR) è
possibile realizzare qualunque rete logica
• NOT
• AND
Y=X
X
X
Z
Y = XZ
X
• OR
Y = X+Z
Z
AUTRONICA
14.25
OR Esclusivo
• Realizzazione dell’OR Esclusivo
X Y U
0 0 0
0 1 1
U  X  Y  XY  X Y
1 0 1
1 1 0
X
U
X
Y
U
Y
AUTRONICA
14.26
Ciclo
• Definizione
• Ciclo: Percorso chiuso che attraversa k blocchi (k ≥ 1) tutti
nella loro direzione di funzionamento
• Osservazioni
• Tutte le reti viste sono prive di cicli
• I blocchi base combinatori sono privi di cicli
• Le funzioni descrivibili dalle tabelle di verità sono tutte prive
di cicli (le uscite sono funzione dei solo ingressi)
• Conclusione
• Tutte le reti logiche composte di blocchi combinatori e prive
di cicli sono rei combinatorie
AUTRONICA
14.27
Sintesi di reti combinatorie
• Sintesi
• data la descrizione ai terminali di una rete combinatoria
• ottenere la struttura in blocchi logici e le relative interconnessioni
• Osservazioni
• il funzionamento della rete deve essere possibile descriverlo
mediante una tabella di verità
• non esiste una sola realizzazione
• per poter scegliere fra le varie soluzioni è necessario definire il
parametro da ottimizzare
• Funzione COSTO
• (numero di blocchi base, ritardo ingresso uscita, uso di particolari
blocchi, ……..)
• VEDERE ESEMPI SUCCESSIVI
AUTRONICA
14.28
Esempio di funzione
• Data la funzione definita dalla Tabella di Verità:
a
b
c
z
0
0
0
1
0
0
1
0
0
1
0
1
0
1
1
0
1
0
0
1
1
0
1
1
1
1
0
1
1
1
1
0
Si ha:
z  a b c  a b c  a b c  a b c  a b c
 a b c  a b c  a b c  a b c  a b c  a b c
   
 a  c   c  b 
z  a  b  c  a  b  c  a  b  c 
 c  a b  c  a b  c  a  b  c  a  c b
AUTRONICA
14.29
Schemi relativi 1
z  a bc  a bc  a bc  a bc  a bc
a
b
c
z
a
a
b
b
c
c
AUTRONICA
14.30

Schemi relativi 2


z  abc  abc  abc

a
b
z
c
AUTRONICA
14.31
Schemi relativi 3
z  c  a b
a
b
z
c
AUTRONICA
14.32
Schemi relativi 4
 
z  c  a b
a
z
b
c

 
z  ac  cb
a
b
c

z
AUTRONICA
14.33
Half Adder
• Somma di due bit
ai bi si ci+1
0
0 0
0
0
1 1
0
1
0 1
0
1
1 0
1
si  ai  bi
ci 1  ai  bi
si
ai
bi
ci+1
ai
bi
AUTRONICA
si
HA
ci+1
14.34
Full Adder 1
• Somma di due bit compreso il Carry
ci ai bi s ci+1
ai ,bi
i
0
0 0 0
0
0
0 1 1
0
0
1 0 1
0
0
1 1 0
1
1
0 0 1
0
1
0 1 0
1
1
1 0 0
1
1
1 1 1
1
ci
00
0
si
1
01
11
1
1
10
1
1
ai ,bi
ci
ci+1
00
01
0
1
AUTRONICA
11
10
1
1
1
1
14.35
Full Adder 2
• Lo schema risulta
si  ai  bi  ci  ai  bi  ci 
ci 1  ai  bi  ai  ci  bi  ci
ai
bi
ci
si
ai
bi
si
FA
ci
ai
bi
ci+1
AUTRONICA
ci
ci+1
si
FA
ci+1
14.36
Sommatore a riporto seriale
(Ripple-Carry Adder)
• Somma di due parole di 4 bit in C. 2
b a
b a
3
2
3
b1 a1
b0 a0
2
c
0
ci
ai
bi
ci
ai
bi
ci
ai
bi
ci
ai
bi
FA
FA
FA
FA
si
ci+1
si
ci+1
si
ci+1
si
ci+1
c
4
s
s2
s1
s0
3
AUTRONICA
14.37
Proprietà dello XOR
• Lo XOR può essere visto come un inverter
“programmabile”
S
in
out
0
0
0
per
S 0
è out  in
0
1
1
1
0
1
per
S 1
è out  in
1
1
0
in
out
S
AUTRONICA
14.38
Considerazioni sulla sottrazione
• Si ricorda che
W  A  B  A   B
• Operando in complemento a 2 si ha

 B  B 1
• Quindi

W  A  B  A  B 1
AUTRONICA
14.39
Sommatore/Sottrattore
• In base alle proprietà dello XOR e come si può eseguire la
differenza (A – B) in C. 2 si ha:
a3
b3
a2
b2
a1
b1
a0
b0
k
A–B K=1
A+B k=0
ci
bi
ai
ci
bi
ai
ci
bi
ai
ci
bi
ai
FA
FA
FA
FA
si
ci+1
si
ci+1
si
ci+1
si
ci+1
c
4
s
3
s2
AUTRONICA
s1
s0
14.40
Conclusioni
•
•
•
•
•
•
•
•
•
•
•
•
Postulati
Principio di dualità
Teoremi fondamentali
insieme funzionalmente completo NAND e NOR
Funzione XOR
Reti logiche combinatorie e sequenziali
Simboli
Concetto di ciclo
Concetto di minimizzazione (funzione costo)
Realizzazioni diverse della stessa funzione
Half Adder e Full Adder
Sommatori di due word di n bit
AUTRONICA
14.41