file

Relatività generale
e oltre
La fisica ed il Cosmo
Fisica 24 ore
1
Principio di equivalenza


Non è possibile distinguere la
gravità dall’accelerazione
Massa inerziale
= massa gravitazionale

G m xi (t )  xi (t )
d 2 xi (t )
m
  m
2
3
j
j
dt
 i
x (t )  x (t )


Gravità può essere descritta in
termini metrici
La fisica ed il Cosmo
Fisica 24 ore
2
Spazio tempo dinamico

Materia determina le lunghezze
La fisica ed il Cosmo
Fisica 24 ore
3
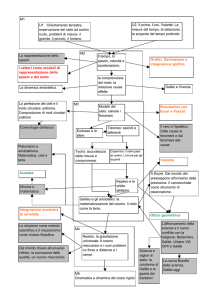
Materia e spazio

Uno può visualizzare la relatività generale
pensando lo spazio tempo come un foglio che in
assenza di materia è piatto ma è curvato della
materia
materia
Sorgente di Curvatura
dello spazio tempo
1
R  g  R  8 G T
2
La fisica ed il Cosmo
Fisica 24 ore
4
Deviazione della luce (lenti)


Effetto gravità equivale ad una
modificazione tessuto spazio
temporale
La luce viene deviata, e quindi
può essere focalizzata, da una
distribuzione di massa
La fisica ed il Cosmo
Fisica 24 ore
5
Buchi neri

Regione delle spazio tempo che
………. intrappola la luce
La fisica ed il Cosmo
Fisica 24 ore
6
Onde gravitazionali


Evidenza indiretta PSR 1913+16
Nobel a Taylor nel 1993
La fisica ed il Cosmo
Fisica 24 ore
7
Einstein ed Oltre Einstein




Onde gravitazionali
Cosa ha dato energia al
BIG BANG
Cosa succede al bordo
di un BUCO NERO
Cosa è l’energia oscura
La fisica ed il Cosmo
Fisica 24 ore
8
Progressi da osservazione con base
nello spazio


Spettroscopia X [Chandra]
Spettroscopia Gamma
[Integral]
La fisica ed il Cosmo
Fisica 24 ore
9
Immagini X (Centro della galassia)
La fisica ed il Cosmo
Fisica 24 ore
10
“Gamma Ray Burst”

Sono gli eventi più energetici
dell’universo
Missione SWIFT NASA
concorrenza con INTEGRAL
La fisica ed il Cosmo
Fisica 24 ore
11
MATERIA OSCURA
1. rilevata solo dai suoi effetti gravitazionali
2. non rientra nel Modello Standard delle particelle elementari
3. uno dei principali costituenti dell’universo?
La fisica ed il Cosmo
“oscura” = non emette luce 12
Fisica 24 ore
effetti gravitazionali - prima evidenza:
materia oscura nelle galassie (Zwicky, 1933)
Keplero:
La fisica ed il Cosmo
Fisica 24 ore
...“massa mancante” 13
effetti gravitazionali - seconda evidenza:
materia oscura nei cluster di galassie
cluster di galassie:
Contengono gas caldo che
emette radiazione X
materia oscura  equilibrio meccanico:
senza materia oscura il gas caldo si dissolverebbe
La fisica ed il Cosmo
Fisica 24 ore
14
effetti gravitazionali - terza evidenza:
lenti gravitazionale
massa alone  forma degli archi
Abell 2218, un cluster di galassie
lontano circa 3 miliardi di anni luce,
piega la luce dalle galassie retrostanti
creando lunghi e deboli archi.
http://ngst.gsfc.nasa.gov/science/gravlens.htm
La fisica ed il Cosmo
Fisica 24 ore
15
Candidati di Materia Oscura
Barionica: materia ordinaria fatta di protoni e neutroni?
Alcune idee:
1. Nane Brune o pianeti tipo Giove
2. Resti di stelle fredde (buchi neri, stelle di neutroni, nane bianche,
3. Buchi neri primordiali (lasciati dopo il Big Bang)
Tutte queste forme di materia oscura barionica sono collettivamente
chiamate Massive Compact Halo Objects (MACHOs)
Non barionica: prodotta nei primi istanti dopo il Big Bang
Alcune idee:
1. Neutrini massivi
2. Nuove particelle esotiche
 oltre il Modello Standard
Tutte queste forme di materia oscura non barionica sono
collettivamente chiamate Weak Interactive Massive Particles
(WIMPs)
La fisica ed il Cosmo
Fisica 24 ore
16
Indagine cosmologica 
?
La fisica ed il Cosmo
Fisica 24 ore
17
INFLAZIONE & ENERGIA OSCURA
dopo il Big Bang...
... e oggi?
COSTANTE COSMOLOGICA
 oltre il Modello Standard?
La fisica ed il Cosmo
Fisica 24 ore
18
Il problema gravitazionale a due corpi
ONDE Gravitazionali
FN 15M
ISCO
FN
CL
FN or CL
+10-21-
tempo
–10-21-
“inspiral”
La fisica ed il Cosmo
Fisica 24 ore
“plunge/merger” “ring-down”
19
LIGO & VIRGO
La fisica ed il Cosmo
Fisica 24 ore
20
L’osservatorio ad Hanford
La fisica ed il Cosmo
Fisica 24 ore
21
GEO600
Hannover
La fisica ed il Cosmo
Fisica 24 ore
22
LISA – LIGO/VIRGO
La fisica ed il Cosmo
Fisica 24 ore
23
LISA

Interferometro con base nello spazio
La fisica ed il Cosmo
Fisica 24 ore
24
Sorgenti gravitazionali per LISA

Sistemi semi-separati di piccolo
periodo
Primaria: nana bianca
Secondaria: una stella che trasferisce materia
alla sua compagnia
La fisica ed il Cosmo
Fisica 24 ore
25
Risolvere numericamente le equazioni
di Einstein
1
R  g  R  0
2
Affettando lo spazio tempo:
Decomposizione 3+1
ds 2   2 dt 2  gij (dxi   i dt )(dx j   j dt )
6 equazioni di evoluzione + 4 vincoli
H  R  K 2  Kij K ij  0
 t ij  2K ij  i  j   j  i
 t K ij  

( 3)
Rij  K ij trK  2 K ik K k j

  i  j   k  k K ij  K ik  j  K jk  i   
D i  i ( K ij  g ij K )  0
Devono essere
soddisfatte dalle
CONDIZIONI INIZIALI
La fisica ed il Cosmo
Fisica 24 ore
26
La forma BSSN delle equazioni di
Einstein nel formalismo Hamiltoniano
~ ~ ~
~ ~
~ ~
Rij   12 g~ lm g~ij,lm  g~k (i  j )  k   k (ij ) k  g~ lm (2lk(i j ) km  imk klj )
RTF
 Rij  13 gij R
ij
 t   K    i   i 
~ ~ ij 1
ij
 t K   g  i  j   ( Aij A  3 K )   i  i K
 g~  2K  g~   k  g~   k  2 g~   k
i
1
6
t
ij
ij
1
6
jk
i
i
ik
j
3
ij
k
~
~
~
~
 t  i  2 A ij  j  2 ( ijk A jk  23 g~ ij  j K  6 A ij  j ) 
~ ~
~
  k  k  i   k  k  i  23  i  k  k  13 g~ ij  j  k  k  g~ jk  j  k  i
~
~
~ ~
 t Aij  e  4 (( i  j )TF  RijTF )   Aij K  2 Aik A k j   i  j 
~
~
~
~
  k  k Aij  Aik  j  A jk  i    23 Aij  k  k




[4] M. Shibata, T. Nakamura: “Evolution of three dimensional gravitational ..”, Phys. Rev. D52(1995)5429
[5] T.W. Baumgarte, S.L. Shapiro: “On the numerical integration of Einstein..”, Phys. Rev. D59(1999)024007
La fisica ed il Cosmo
Fisica 24 ore
27
Schwarzschild in coordinate di Novikov
• “geodesic
slicing”:
Osservatore in caduta libera
lapse = 1, shift = 0
codice fallisce per  = m
grr
• “singularity avoiding
slicing”
shift = 0
• black hole
La fisica ed il Cosmo
Fisica 24 ore
28
Collisione di due buchi neri





I dati iniziali corrispondono a due buchi neri non
rotanti
La simulazione parte dall’ISCO
La gravitazionale emessa è mostrata dai colori
L’orizzonte degli eventi dei
buchi neri è mostrata come
una superficie scura.
Compiono circa un
1/3 di orbita prima di unirsi.
http://www.eu-network.org/Documents/Movies.html
La fisica ed il Cosmo
Fisica 24 ore
29
Ricerche a Parma:
Il progetto Albert100 (OG51)



La rivelazione delle onde gravitazionali si avvicina
I Fisici sperimentali hanno bisogno di “templates”
Non c’erano (in ITALIA) risorse computazionali
dedicate alla relatività numerica
Ferrara
Padova
Parma
Fortini Pierluigi
Fernando De Felice, Gianluca Genelli, Francesco Sorge
Roberto De Pietri, Francesco Di Renzo, Alessandro Nagar,
Enrico Onofri
Roma 1
Omar Benhar Noccioli, Valeria Ferrari, Leonardo Gualtieri,
Giovanni Minutti, Josè Pons
Trieste (Sissa) Luca Baiotti, Antonio Lanza, Luciano Rezzolla, John Miller,
Pedro Montero
La fisica ed il Cosmo
Fisica 24 ore
30
Il nostro sistema



44 nodi IBM e-server 330
88 Pentium III 1,133 GHz
1.5 GBytes RAM per nodo
La fisica ed il Cosmo
Fisica 24 ore
31
Accrescimento quasi periodico e onde
gravitazionali da una stella di neutroni toroidale
oscillante
Collaborazione di
L. Rezzola, O. Zanotti and T. Font.
Dettagli: gr-qc/0210018



Viene mostrata l’evoluzione della densità di massa a riposo della
stella di neutroni toroidale
Il calcolo è stato effettuato con codice idrodinamico relativistico
in 2D usando coordinate polari.
Lo spazio-tempo del buco nero è ottenuto come una sequenza di
stati quasi stazionari di soluzioni di Schwarzschild con massa che
si incrementa.
La fisica ed il Cosmo
Fisica 24 ore
32
Benchmarks

Griglia locale 40x40x40
Prova di velocità standard BenchADM



Evoluzione della metrica piatta di
Minkowski
100 passi di evoluzione temporale
Tempi di esecuzione in secondi

Simulazioni non lineari in 3D

GRIGLIA (Np=64) ~ 270x270x270
150
100
GNU
Intel
50
0
1
8
16
27
64
Griglia locale 70x70x70
600
400
 t ij  2K ij  i  j   j  i
 t K ij  i  j   k  k K ij  K ik  j  K jk  i   


( 3)
Rij  K ij trK  2 K ik K k j
La fisica ed il Cosmo

Fisica 24 ore
GNU
Intel
200
0
1
8
16
27
64
33
………
Sistema
Origin 2000
Griglia
NP
time
NP
Intel
GNU
40x40x40
1
14.08
37.93
40x40x40
8
18.80
42.80
40x40x40
16
30.41
50.63
40x40x40
64
61.45
82.50
70x70x70
1
85.56
220.00
70x70x70
8
101.07
235.02
64
41.38
Cray T3E (600MHz)
816
44.66
IBM SP2 (Power3)
1152
14,15
PentimIV 1,7GHz
2
10,20
70x70x70
16
112.94
247.41
EV6 Alpha21264A
1
9.72
70x70x70
27
128.14
260.36
1024
17,66
70x70x70
64
176.27
302.77
PIII Cluster NCSA
Griglia
albert vs. altri
Griglia 40x40x40 su
1 nodo di calcolo
NP
Albert
Platinum
40x40x40
1
14.0 (100%)
23.2 (100%)
40x40x40
8
18.8 ( 74%)
28.5 ( 81%)
40x40x40
16
30.4 ( 46%)
29.0 ( 80%)
40x40x40
64
61.4 ( 23%)
30.5 ( 76%)
www.cactuscode.org/Benchmark/Results.html
La fisica ed il Cosmo
Fisica 24 ore
34
Tempi di esecuzione per BSSN

Evoluzione del tipo BSSN








Grid SIZE
Evoluzione della metrica piatta
di Minkowski
100 passi temporali
Tempo di esecuzione in sec
Evoluzione temporale: ICN a
tre passi
Lapse: affettamento 1+log
Shift: ‘delayed’ Gamma
freezing
Simulazione non lineare 3D
Griglia (Np=64) 308x308x148
La fisica ed il Cosmo
Fisica 24 ore
NP
Time
80x80x40
1
1438
80x80x76
2
1853
80x156x76
4
2131
156x156x76
8
2230
156x156x148
16
2791
156x232x148
24
3046
156x308x148
32
3174
232x308x148
48
3493
308x308x148
64
3487
35