punti notevoli di un triangolo

PUNTI NOTEVOLI DI UN
TRIANGOLO





Baricentro
Incentro
Ortocentro
Circocentro
Animazioni realizzate con Macromedia
Flash
BARICENTRO
Cominciamo con la costruzione del
baricentro di una qualunque figura
piana:
Seleziona questo link
http://www.youtube.com/watch?v=yQFI0
SdCPK4

Ricapitoliamo



Il baricentro è il punto di intersezione di
due verticali col filo a piombo in cui un
corpo resta in equilibrio
Vale per tutte le figure piane e quindi
anche per i triangoli
Ma il baricentro è anche ….
Il punto di intersezione delle
mediane


Mediana : segmento condotto da un
vertice al punto medio del lato opposto
Baricentro : punto di intersezione delle
mediane
Costruzione del baricentro di un
triangolo
Costruiamo il triangolo ABC e i punti medi dei
tre lati . Siano essi M,N e O
A
M
Disegniamo le tre mediane AO, BN e CM
N
G
C
B
Il punto di intersezione delle tre mediane
G
è il baricentro del triangolo
O
Provate a costruire un triangolo con un cartoncino,
a disegnare le mediane e appoggiate il triangolo nel punto G
su di un dito o una matita anche appuntita
Troverete che resta perfettamente in equilibrio
Incentro


Punto di intersezione delle bisettrici ma
anche ….
Centro del cerchio inscritto
A
Incentro
Disegniamo un triangolo ABC
Disegniamo ora le tre bisettrici
( che dividono gli angoli in due parti uguali)
K
K
B
Esse si incontrano nel punto K (incentro)
che è anche il centro del cerchio inscritto
C
Ortocentro:
punto di intersezione delle altezze
Disegniamo il triangolo ABC
A
E le tre altezze AD , BE, CF
E
F
O
B
C
D
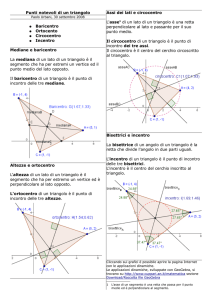
Circocentro : intersezione degli
assi


Circocentro : intersezione degli assi, ma
anche centro del cerchio circoscritto
Asse di un segmento : perpendicolare
nel punto medio del segmento
Circocentro
Disegniamo un triangolo ABC
A
Disegniamo i tre assi dei tre lati
M
PP
B
N
O
Il punto di intersezione P (circocentro)
è anche il centro del cerchio circoscritto
C
Animazioni realizzate con
Macromedia Flash




Baricentro
Ortocentro
Incentro
Circocentro