Di Andrea Tellini
cl. 4^H
a.s. 2003-2004
Alcuni strani fenomeni…
Nell’esperimento sulla trasmissione della luce
abbiamo usato anche delle lenti polaroid e
avevamo notato che c’era un’anomalia: non tutti i
punti seguivano la legge esponenziale che
descrive il fenomeno per tutti gli altri materiali.
Ecco cosa avevamo ottenuto con questo
particolare tipo di lenti.
Dati raccolti e rielaborati
intensità
relativa
±1
I0
22,7
±0,3
I1
2
9,6
±0,2
I2
3
3,7
±0,1
I3
0
96
1
Intensità trasmessa (polaroid non
incrociati)
Intensità relativa
(%)
numero
lenti
y = 83,064e-1,0795x
R2 = 0,9875
150
100
50
0
0
1
2
3
Numero polaroid
Conclusioni derivanti dall’analisi dei dati:
•Non viene rispettata la legge I I0 ekx
(infatti il rapporto tra punti
successivi del grafico non è costante
• Tale rapporto ( I n1 ) è costante entro gli errori sperimentali solo per n>0,
In
invece, sempre entro gli errori sperimentali,
I
I
I
2 3 k 2 1.
I
I
I
1
2
0
•L’azione di questo tipo di materiale (polaroid) deve essere diversa da quella
degli altri.
4
Cosa succede allora?
I polaroid compiono sulla luce un’azione detta polarizzante.
In che cosa consiste?
La luce, come ogni onda elettromagnetica, è trasversale (la
vibrazione è perpendicolare alla direzione di propagazione).
Il campo elettrico generato da quest’onda è oscilla
perpendicolarmente rispetto al piano di propagazione. Se il
campo magnetico viene “costretto” in qualche modo a
oscillare lungo solo un piano fisso, allora la luce si dice
polarizzata linearmente.
Come si può ottenere la luce polarizzata?
Con uno dei seguenti metodi:
•Assorbimento
•Riflessione
•Diffusione
•Birifrangenza
Polarizzazione per assorbimento
È il caso dei polaroid, o comunque dei materiali che fungono da lamine
polarizzatrici. I polaroid sono formati da lunghe catene idrocarburiche
che vengono allineate e stirate in una direzione durante il processo di
fabbricazione. La luce viene così “costretta” ad attraversare il polaroid
solo parallelamente alla direzione lungo cui le catene vengono stirate.
Questa direzione è detta asse di trasmissione.
Osserviamo cosa succede ruotando due polaroid uno rispetto all’altro.
L’intensità della luce trasmessa varia a seconda dell’angolo di
rotazione tra un massimo e 0 (in questo caso, che si ottiene con una
rotazione di 90°, non passa luce), con periodicità di 180°. Se però tra
due lenti poste in modo che non passi luce inseriamo una terza lente,
l’intensità trasmessa non è più 0.
Si può quindi ipotizzare che l’intensità trasmessa vari in funzione
dell’angolo con cui sono ruotati i polaroid.
Cerchiamo quindi questa legge (vai alla scheda dell’esperimento)
INDIETRO
Alla ricerca della legge di Malus
Materiale: due lenti polaroid fissate su un sostegno rotante graduato; sorgente
luminosa qualsiasi (nel nostro caso lampadina a filamento incandescente);
sensore di intensità luminosa collegato al copmuter tramite interfaccia.
Procedimento: allineati la sorgente di luce, i due polaroid e il sensore (la
distanza di questo dalla sorgente deve essere mantenuta costante, altrimenti va
considerata anche la legge dell’inverso quadro della distanza), si effettuano le
misure dell’intensità trasmessa ruotando man mano solo una polaroid.
Decidiamo di attribuire all’angolo per cui si ha l’intensità massima il valore 0 (in
questo caso gli assi di trasmissione sono paralleli).
Dati raccolti:
angolo in gradi
Intensità
0
6,4
10
5,9
20
5,7
30
5,2
40
4,3
50
3
60
2,4
70
1,9
80
1,7
90
1,6
Elaborazione dati: tracciamo il
grafico dell’intensità in funzione
dell’angolo relativo di inclinazione
tra gli assi di trasmissione. Vai al
grafico
I=f(α)
Ecco il grafico dell’intensità in funzione
dell’angolo.
7
6
Intensità
5
4
3
2
1
0
0
20
40
60
80
100
α
Si può ipotizzare un andamento
cosinusoidale. Tracciamo quindi il
grafico dell’intensità in funzione del
coseno dell’angolo.
I=f(cos α)
Ecco il grafico dell’intensità in funzione
del coseno dell’angolo.
y = -0,0001x 2 - 0,0022x + 1,014
R2 = 0,999
1
0,8
Intensità
Si può ipotizzare un andamento
parabolico. Tracciamo quindi il grafico
dell’intensità in funzione del quadrato
del coseno dell’angolo.
1,2
0,6
0,4
0,2
0
-0,2
0
20
40
60
80
100
cos α
I=f(cos 2 α)
Ecco il grafico dell’intensità in funzione
del quadrato del coseno dell’angolo. La
correlazione è ora, nell’ambito degli
errori sperimentali, lineare.
7
6
Intensità
5
4
3
y = 4,8304x + 1,3947
R2 = 0,9887
2
1
0
0
0,2
0,4
0,6
cos 2 α
0,8
1
1,2
Vediamo cosa possiamo concludere
Le ipotesi sono state confermate nell’ambito degli errori
sperimentali. La funzione ha periodicità di π, dato che conferma
così l’analisi fenomenica.
La legge che descrive il fenomeno può essere espressa secodo
la forma
2
I I cos
0
dove I0 è l’intensità che investe il polaroid, mentre α l’angolo
relativo tra gli assi di trasmissione. Tale legge è detta legge di
Malus.
L’angolo può essere solo relativo, perché avendo a disposizione
solo un polaroid (detto polarizzatore) non è determinabile l’asse
di trasmissione in modo assoluto. È necessario infatti disporre di
un secondo polariod (analizzatore) per determinarlo.
Proponiamo ora l’interpretazione di tale legge.
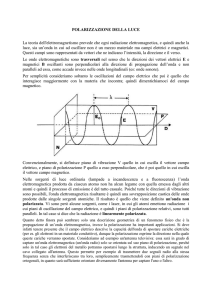
Abbiamo già detto che l’onda elettromagnetica luminosa presenta un
campo elettrico che vibra in un piano perpendicolare alla direzione di
propagazione dell’onda. Il vettore campo elettrico può quindi essere
scomposto in due componenti, come nella seguente figura:
Nella figura l’asse di propagazione dell’onda è quello z (non disegnato),
perpendicolare allo schermo.
Dopo la polarizzazione solo una delle componenti del vettore campo
elettrico rimane, per esempio Ex, cioè E·cos α. L’intensità di un’onda
dipende dal quadrato dell’ampiezza. Nell’equazione di un’onda
elettromagnetica l’ampiezza viene sostituita con il vettore campo elettrico,
quindi l’intensità è proporzionale al quadrato del vettore campo elettrico.
Quindi I=k·E2=k·E02·cos2 α, da cui la diretta proporzionalità tra l’intensità e
il quadrato dell’angolo.
INDIETRO
Polarizzazione per riflessione
Se si guarda la luce riflessa da un davanzale o dal pavimento a grandi angoli
tramite una lente polaroid, si vede variare l’intensità della luce trasmessa. Ciò
significa che la luce è perlomeno parzialmente polarizzata.
Vediamo cosa succede...
Abbiamo già detto che il campo elettrico dell’onda luminosa oscilla sugli infiniti
piani perpendicolari alla direzione di propagazione. Il vettore campo elettrico può
essere scomposto in due componenti: una parallela al piano identificato da
raggio incidente, raggio riflesso e normale al piano di incidenza e una
perpendicolare a questo piano. Dopo la riflessione la componente parallela è
ridotta (anche la luce rifratta è polarizzata: in questo caso però si riduce la
componente perpendicolare del campo elettrico). Esiste un angolo per cui la
componente parallela riflessa è nulla. Tale angolo è detto angolo di Brewster (qui
lo indicheremo come θB e verifica le seguenti condizioni:
•θincidenza=θB
•θrifratto+θincidenza=90°
Quest’ultima relazione è difficile da spiegare, essendo necessarie nozioni di
magnetismo.
SEGUE
Per la legge di Schnell-Cartesio della rifrazione si ha:
sin
n
incidenza 2
n
sin
1
rifrazione
Applicando le proprietà dell’angolo di Brewser sopra elencate a tale
relazione si ottiene:
n
sin
sin
B
B
tan 2
B n
sin(90 ) cos
B
1
B
Abbiamo anche realizzato un esperimento per determinare l’angolo
di Brewster per il vetro (vai alla scheda dell’esperimento).
INDIETRO
Esperimento sull’angolo di Brewster
Materiale: sorgente di luce non polarizzata (nel nostro caso lampadina a
filamento), la cui luce è collimata con degli appositi strumenti ottici; una piccola
lastra di vetro (per esempio vetrino da microscopio); goniometro; sensori di
intensità luminosa, una lente polaroid.
Montaggio del materiale: far convergere un sottile pennello di luce sulla
superficie riflettente (vetro) attraverso opportuni strumenti ottici (diaframma)
posizionata su un goniometro e mettere un sensore di intensità luminosa in modo
da intercettare il raggio (o meglio il pennello) riflesso. Porre quindi la lente
polaroid tra la superficie riflettente e il sensore di intensità.
Procedimento: per ogni angolo di incidenza effettuare la misurazione
dell’intensità trasmessa dal polaroid, ruotando questo di almeno 180°. Cambiare
quindi l’angolo di incidenza ed effettuare nuovamente la misura.
Elaborazione dati: essendo la luce riflessa parzialmente polarizzata, l’intensità
trasmessa varia al variare dell’angolo di rotazione del polaroid. Indichiamo con R
il grado di polarizzazione della luce definito come
l’intensità massima trasmessa e Imin quella minima.
Riportiamo in un grafico i risultati ottenuti.
dove Imax è
Conclusioni: l’angolo di Brewster per il vetro usato è compreso tra 55°
e 60°, essendo il grado di polarizzazione relativo pari al 100%. Tale
dato è compatibile con quelli forniti dalla letteratura (circa 57° per il
vetro comune).
La precisione dell’esperimento non può essere migliorata data la
limitata precisione del sensore di intensità.
INDIETRO
Polarizzazione per diffusione
Spiegare il motivo per cui la luce diffusa è polarizzata è complicato,
perché richiede nozioni complesse di elettromagnetismo.
Accontentiamoci allora di alcune osservazioni.
•Analizzando con un polaroid la luce emessa direttamente il sole
vediamo che non è polarizzata perché ruotando il polaroid
l’intensità trasmessa non varia.
Ruotiamoci ora di 90° e analizziamo la luce diffusa: questa è invece
polarizzata parzialmente (infatti l’intensità trasmessa non è mai
nulla.
•Lo stesso fenomeno è sperimentabile osservando, sempre
perpendicolarmente rispetto alla direzione di propagazione, la luce
diffusa da un bicchiere contenente una soluzione di acqua e
zucchero
INDIETRO
Polarizzazione per birifrangenza
Esistono in natura dei materiali anisotropi, ovvero il cui comportamento
rispetto a certi fenomeni varia a seconda della direzione del materiale.
Per esempio in alcuni materiali (quali la calcite o lo spato d’Islanda) la
velocità della luce che lo attraversa non è uguale per tutte e tre le
direzioni spaziali.
Quando un raggio luminoso incide su tali sostanze, esso può separarsi
in due raggi, detti ordinario (quello che segue la legge della rifrazione
di Schnell-Cartesio) e straordinario (quello che non segue tale legge).
Esiste però una direzione per la quale i due raggi si propagano con la
stessa velocità e quindi coincidono. Questa direzione è detta asse
ottico del materiale.
Se la luce incidente forma un angolo con l’asse ottico si formano
appunto raggio ordinario e straordinario, che sono polarizzati in
direzioni mutuamente perpendicolari: infatti ruotando un polaroid
analizzatore viene trasmesso prima l’no e dopo l’altro raggio,
precisamente ogni 90° di rotazione.
INDIETRO