Tecnologie Astronomiche

Tecnologie Astronomiche
M. Brescia
Modello di una lente in Zemax - 15
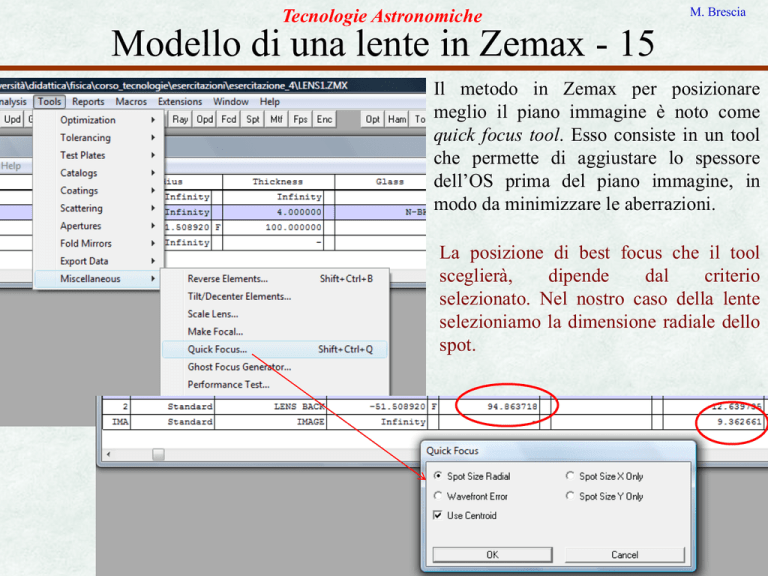
Il metodo in Zemax per posizionare
meglio il piano immagine è noto come
quick focus tool. Esso consiste in un tool
che permette di aggiustare lo spessore
dell’OS prima del piano immagine, in
modo da minimizzare le aberrazioni.
La posizione di best focus che il tool
sceglierà,
dipende
dal
criterio
selezionato. Nel nostro caso della lente
selezioniamo la dimensione radiale dello
spot.
Tecnologie Astronomiche
Modello di una lente in Zemax - 16
Osserviamo già i miglioramenti in termini di defocus
M. Brescia
Tecnologie Astronomiche
Modello di una lente in Zemax - 17
le dimensioni geometriche e RMS degli spot si sono ridotte di un fattore 2!
M. Brescia
Tecnologie Astronomiche
M. Brescia
Modello di una lente in Zemax - 18
Ma ancora il sistema è migliorabile. Qui si innesca il processo ciclico di ottimizzazione,
preceduto da 2 importanti steps:
• selezionare i parametri liberi e quelli fissati (gradi di libertà dell’OS);
• selezionare e costruire la funzione di merito (MF);
Il parametro Radius della LENS BACK è stato fissato. Dunque abbiamo la possibilità di variare:
• spessore della lente;
• il raggio di curvatura della lente;
• distanza dal retro-lente al piano immagine, cioè il thickness della surface 2;
Per istruire Zemax su quali siano i gradi di libertà su cui poter agire, basta farli diventare variable
Tecnologie Astronomiche
Modello di una lente in Zemax - 19
Ecco dunque le variabili su cui la funzione di merito agirà:
Ora costruiamo la MF: esiste uno specifico editor della MF, chiamato MFE. Apriamolo:
M. Brescia
Tecnologie Astronomiche
M. Brescia
Modello di una lente in Zemax - 20
Scegliamo la MF di default, dato che a noi interessa l’ottimizzazione in termini di raggio RMS
dello spot rispetto al centroide dell’immagine, cosa già implicita nella MF di default.
M. Brescia
Tecnologie Astronomiche
Modello di una lente in Zemax - 21
Dal menu Tool, si può selezionare “Optimization” per lanciare il panel di comando che attiva il
processo ciclico di ottimizzazione. Notare il prima e dopo aver premuto “Automatic”.
PRIMA
DOPO
Tecnologie Astronomiche
M. Brescia
Modello di una lente in Zemax - 22
Valutazione finale
RMS e GEO radius è sceso di un fattore 10!
Tecnologie Astronomiche
Modello di una lente in Zemax - 22
Certamente non abbiamo ottenuto un OS perfetto, ma la specifica è stata rispettata.
M. Brescia
Tecnologie Astronomiche
M. Brescia
PSF in Zemax - 1
La PSF di un sistema ottico è la distribuzione d’intensità della sorgente. Come sappiamo, sebbene
si possa approssimare la sorgente ad un punto, in realtà non lo è. Primo perchè le aberrazioni
allargano l’immagine su un’area finita. Secondo perchè, anche in assenza di aberrazioni, vale il
limite di diffrazione.
ZEMAX fornisce la possibilità di calcolare la PSF in 3 modi:
1. geometric (no diffraction) spot diagram (dominio spaziale)
2. diffraction based FFT (dominio in frequenza)
3. Huygens PSF (dominio di fronte d’onda)
Tecnologie Astronomiche
M. Brescia
Spot Diagram: una PSF geometrica - 1
Come abbiamo già visto, lo Spot Diagram proietta i raggi da una singola sorgente attraverso l’OS
e visualizza le coordinate (x,y) dei raggi sul piano.
Qui è mostrato un esempio relativo ad uno specchio parabolico F/5 con lunghezza focale di
50mm. Il sistema rappresenta un telescopio newtoniano.
Tecnologie Astronomiche
M. Brescia
Spot Diagram: una PSF geometrica - 2
Il diagramma indica chiaramente la presenza di coma e astigmatismo fuori asse. Peraltro in asse il
sistema è invece perfetto. Lo si può vedere meglio se selezioniamo la visualizzazione del disco di
Airy nel diagramma:
Tecnologie Astronomiche
M. Brescia
FFT PSF - 1
In asse lo spot è molto più piccolo del disco di Airy, diversamente dal fuori asse. Ciò indica che
lo spot diagram è un utile strumento per valutare le prestazioni su tutto il campo.
La Fast Fourier Transform (FFT) è un algoritmo ampiamente utilizzato nell’analisi in frequenza
di molti sistemi elettronici e ottici. Concettualmente esso decompone una distribuzione di energia
spaziale in una distribuzione nello spazio in frequenza.
La FFT PSF di un OS si effettua tracciando una griglia di raggi dalla sorgente alla pupilla di
uscita. Per ogni raggio, l’ampiezza e la differenza di cammino ottico sono usate per calcolare
l’ampiezza di un punto del fronte d’onda in corrispondenza della pupilla di uscita. La FT di
questa griglia, viene poi scalata e quadrata per generare la PSF.
In Zemax è sufficiente selezionare:
Analysis > PSF > FFT PSF
Tecnologie Astronomiche
FFT PSF - 2
Questo è un altro modo per visualizzare la FFT PSF
M. Brescia
Tecnologie Astronomiche
M. Brescia
Huygens PSF - 1
La Huygens PSF è calcolata convertendo ogni raggio dello Spot Diagram in una piccola onda.
Ricordiamoci infatti che un raggio in Zemax modella una piccola porzione di onda piana e che il
raggio localmente è normale al fronte d’onda. L’onda piana ha un’ampiezza, una fase e una
direzione determinate dai dati associati al raggio che la genera. L’intensità totale di un punto della
superficie dell’immagine può essere determinata sommando tutte le onde piane relative a tutti i
raggi tracciati.
La Huygens PSF non è basata sulla FFT ed è di solito più lenta nel calcolo, ma più accurata nei
casi in cui, ad esempio, si è sotto il limite di campionamento di Nyquist o quando in generale:
• La superficie dell’immagine è estremamente tiltata rispetto al chief ray;
• Vi è un’eccessiva distorsione tra pupilla d’entrata e d’uscita;
M. Brescia
Tecnologie Astronomiche
Huygens PSF - 2
La Huygens PSF di un OS si calcola tracciando una griglia di raggi sul piano immagine. Per ogni
raggio, l’ampiezza, le coordinate, i coseni direttori e la differenza di cammino ottico sono usati
per calcolare l’ampiezza dell’onda piana incidente su ogni punto della griglia (piano immagine).
In Zemax è sufficiente selezionare Analysis > PSF > Huygens PSF
I principali parametri sono: Pupil Sampling, Image Sampling, and Image Delta.
Image Delta è la distanza tra due punti consecutivi nella griglia (in micron). La regione totale in
cui è calcolata la H-PSF non è altro che il prodotto Image Delta x Image Sampling
on axis
off axis
Tecnologie Astronomiche
M. Brescia
Sistemi Off-axis in Zemax - 1
ZEMAX può anche modellare sistemi ottici off-axis, che cioè contengono folding mirror,
componenti ottiche tiltate rispetto all’asse ottico.
Per fare ciò si introducono nel disegno ottico le superfici di tipo "Coordinate Break”.
Una Coordinate Break (CB) permette di specificare lo shift in x,y o in z e/o il tilt (rotazione
intorno all’asse ottico) della successiva superficie. Essa è pertanto una “dummy surface”, cioè
non ha alcun potere riflettivo o rifrattivo.
Tecnologie Astronomiche
M. Brescia
Sistemi Off-axis in Zemax - 2
Ad esempio consideriamo un gregoriano con 2 specchi conici. Se non introducessimo uno shift
fuori asse, otterremmo il totale oscuramento sul piano immagine (per costruzione delle ottiche
introdotte).
Tecnologie Astronomiche
M. Brescia
Sistemi Off-axis in Zemax - 3
Viceversa, definendo uno spostamento (decenter), mediante un coordinate break, si riesce ad
ottenere un fascio collimato verso il piano immagine
Tecnologie Astronomiche
M. Brescia
ottica attiva/adattiva - 1
Gli strumenti di ray tracing possono giocare un ruolo importante anche nella fase di progettazione
e verifica dei sistemi di correzione attiva delle ottiche di un telescopio. Prima di vedere come,
dobbiamo però analizzare quali sono i sistemi di correzione previsti.
Storicamente, l’ottica adattiva nasce negli anni ‘50 come idea per risolvere “real time” i problemi
legati all’atmosfera. E’ invece degli anni ‘70 l’idea dell’ottica attiva come soluzione ai
disallineamenti delle ottiche dei grandi telescopi.
Sorgenti di degradazione immagine con relativi tempi scala
Tecnologie Astronomiche
M. Brescia
ottica attiva/adattiva - 2
In generale, i sistemi attivi e adattivi hanno primariamente introdotto i seguenti vantaggi:
• tolleranze ottiche e strutturali sulle superfici ottiche meno stringenti;
• specchi più leggeri e flessibili, quindi meno costosi;
• ridotti drasticamente i problemi termici (minore massa  minore capacità termica);
• auto-gestione (forte automazione) del telescopio attraverso i loop di controllo;
Tecnologie a confronto
Tecnologie Astronomiche
M. Brescia
ottica attiva/adattiva - 3
Il principio di funzionamento in entrambi i casi è lo stesso: il sistema è composto da un tasduttore
di fronte d’onda captato dal telescopio mediante un computer dedicato che, dal feedback del
trasduttore, comanda la possibile correzione da parte dei sistemi installati ad hoc sulle ottiche.
Control loop adattivo
Control loop attivo
M. Brescia
Tecnologie Astronomiche
ottica adattiva
Nel caso dell’ottica adattiva, i parametri fondamentali in gioco sono: il parametro di Fried, ossia
la dimensione della pupilla d’entrata entro cui sussiste correlazione del fronte; l’angolo
isoplanatico, che definisce il FOV entro cui i difetti presenti tra 2 oggetti risulterebbero
indistinguibili; il numero di sub-aperture, cioè quanto densamente campionare il fronte d’onda
distorto; il tempo di correzione, ossia la velocità di risposta del correttore.
 seeing  1.22
0

r0
  0.2
 6/5
D
N  
 r0 
r0

vvento
2
Caso telescopio
con pupilla da 8m
R0
θ0
<h>
ANGOLO ISOPLANATICO:
E’ L’ANGOLO ENTRO CUI
POSSO SPAZIARE SENZA
CHE IL FRONTE D’ONDA
SIA PIU’ ABERRATO DI R0
Tecnologie Astronomiche
M. Brescia
ottica attiva
Nel caso dell’ottica attiva, la correzione avviene direttamente sulle ottiche primarie del
telescopio, tramite attuatori che deformano su tempi di scala lunghi il profilo del fronte d’onda.
•
Rendendo attivo M2 si possono correggere defocus e
coma:
Per il defocus si sposta M2 lungo l’asse ottico
Per il coma si ruota M2 intorno al centro di curvatura
•
Rendendo attivo M1 si possono correggere sferica,
astigmatismo, tricoma, etc.
Tecnologie Astronomiche
M. Brescia
Sensore di fronte d’onda - 1
Cuore del sistema in retro-azione, comune alle 2 tecniche di correzione ottica, è il sensore di
fronte d’onda. Il più comune è lo Shack-Hartmann (SH).
L’idea (Hartmann) consiste nel collocare davanti al telescopio uno schermo con molti fori.
Dall’analisi dell’immagine creata dai raggi passanti prima (intrafocale) e dopo (extrafocale) il
piano focale, si può risalire alla direzione della sorgente per ogni foro. L’evoluzione dell’idea
(Shack) consiste nel suddividere la pupilla d’ingresso in N porzioni con una griglia di piccole
lenti generanti ciascuna l’immagine dell’oggetto osservato (occorre notare la difficoltà
tecnologica nel costruire lenti di circa 1mm di diametro con focale di 100-150mm). Ogni lente
produce un’informazione sul fronte incidente sulla corrispondente sezione della pupilla. Dagli
spostamenti relativi delle singole immagini si può risalire alla deformazione completa del fronte.
Questo viene quindi decomposto nei polinomi (ad es. di Zernike) calcolando quindi le aberrazioni
presenti.
Tecnologie Astronomiche
M. Brescia
Sensore di fronte d’onda - 2
Un’aberrazione è definita positiva se il fronte d’onda reale è al di sopra di quello di riferimento.
Un’aberrazione positiva implica uno shift dello spot di SH verso l’asse ottico.
Le forze di M1 e gli spostamenti di M2 da applicare devono ovviamente avere il segno opposto
rispetto alle aberrazioni misurate dal sensore di fronte d’onda.
Tecnologie Astronomiche
Sensore di fronte d’onda - 3
Passaggio dal sistema di riferimento CCD a quello delle ottiche
Il sensore di fronte d’onda fornisce valori nel sistema di riferimento del
CCD. Ma esso ruota con l’asse di derotazione di campo rispetto agli
specchi che invece sono fissi. Occorre dunque effettuare una
trasformazione di coordinate per applicare forze e spostamenti,
rispettivamente a M1 e M2. Ciò si può fare mediante un cambio
intermedio di coordinate dal sistema CCD a quello dell’asse solidale
con il derotatore di campo e successivamente al sistema di M1/M2.
Sistema AD/ROT
bottom view
(dal piano immagine)
Sistema CCD
bottom view
(dal piano immagine)
Sistema M1
bottom view
(dal piano immagine)
M. Brescia
Tecnologie Astronomiche
M. Brescia
Sensore di fronte d’onda - 4
Esistono anche altri tipi di sensori di fronte d’onda:
• sensore di curvatura: confronta le immagini prima e dopo il p. f. per risalire al fronte d’onda;
• shearing interferometry: si basa sull’interferenza del fronte con se stesso dopo averlo traslato;
Tutti questi metodi sono costretti a
misurare singolarmente soltanto alcune
piccole zone dell’apertura del telescopio,
tanto più piccole e numerose quanto più si
vuole andare a fondo nello sviluppo di
Zernike, perciò il problema della
magnitudine limite (luce debole), diventa
ancora più importante.
Tecnologie Astronomiche
M. Brescia
Laser Guide Star - 1
Una soluzione del tutto innovativa è stata trovata a questo problema nella metà degli anni ’80 e
consiste nel sovrapporre alla sorgente in osservazione una stella artificiale proiettata da un laser
coassiale al telescopio stesso (Laser Guide Star): il raggio laser, regolato (ad es.) sulla lunghezza
d’onda del sodio a 589 nm, percorre in questo modo lo stesso tratto di atmosfera percorso dalla
luce dell’oggetto, quindi raggiunge lo strato di sodio mesosferico a 90km di altezza dal suolo e ne
eccita la fluorescenza lungo un cilindro di atmosfera
di circa 11 km di spessore e 50 cm di diametro, pari ad 1”
alla distanza dello strato. Questo volume di atmosfera
riemette luce di fluorescenza in tutte le direzioni, parte di
questa luce torna verso il telescopio ripercorrendo una
seconda volta l’atmosfera inferiore con l’intensità di una
stella di 6a mag e viene usata come riferimento dal
sistema di correzione ottica.
M. Brescia
Tecnologie Astronomiche
Laser Guide Star - 2
La stella guida laser (LGS) è in grado di misurare tutti gli ordini superiori al primo dello sviluppo
di Zernike del fronte d’onda deformato in entrata all’apertura del telescopio. Non può tuttavia
essere usato per determinare il Tip-Tilt dell’immagine, in quanto in tal caso i raggi di ritorno dalla
stella artificiale ripercorrono lo stesso cammino del fascio laser inviato da terra (a), perciò il
baricentro dell’immagine stellare resta sempre centrato sull’asse ottico. Nelle deformazioni di
ordine superiore invece, le distorsioni causate nei due percorsi di andata e di ritorno si sommano
l’una all’altra (b)
-COSTI ELEVATISSIMI
-DIFFUSIONE ALL’INTERNO
DELLA CUPOLA
-STELLA NON PUNTIFORME
-NON SI PUO’ CORREGGERE PER
TIP- TILT
-I TELESCOPI SONO OTTIMIZZATI
PER IMMAGINI DALL’INFINITO,
NON DAL FINITO
a)
b)
Tecnologie Astronomiche
M. Brescia
Alternativa: stella reale di riferimento - 1
Loop adattivo con stella reale di riferimento
Tecnologie Astronomiche
M. Brescia
Alternativa: stella reale di riferimento - 2
Loop attivo con stella reale di riferimento
Tecnologie Astronomiche
M. Brescia
Problema: vignetting
La soluzione di adottare la stella reale come
riferimento per la correzione ottica ha un
problema: lo specchio usato per deflettere la luce
verso il sensore di fronte d’onda può vignettare il
FOV dello strumento primario (fuoco del
telescopio).
Tecnologie Astronomiche
M. Brescia
Soluzione: off-axis guide star
La soluzione è allora utilizzare il sistema di guida off-axis del telescopio. La stella usata per la
guida può essere rediretta verso il sensore di fronte d’onda per l’analisi del fronte.
Tecnologie Astronomiche
Il sistema di controllo di ottica attiva
M. Brescia
Tecnologie Astronomiche
M. Brescia
ottica attiva con M1 - 1
Per ottica attiva applicata al primario di un telescopio, si intende tenere sotto controllo la forma
dello specchio, che può essere soggetta a deformazioni non uniformi, rispetto all’intera superficie
(specie per specchi di grande diametro e molto sottili), dovute a gradienti termici/gravitazionali,
contro-deformando zone localizzate della superficie prima (off-line) o durante (on-line) le
osservazioni.
Come già detto, ciò può essere fatto mediante un sensore di
fronte d’onda e scomponendo la funzione di fronte d’onda nel
polinomio i cui coefficienti sono i contributi di aberrazione,
di diversa tipologia a seconda del grado nel polinomio.
Abbiamo anche visto che i polinomi di Zernike sono i più
usati. Dai coefficienti di aberrazione si può calcolare la forza
da applicare agli attuatori per attuare la deformazione. Ciò
può essere fatto:
1)
off-line: forze di calibrazione per correggere 1nm di
ogni tipo di aberrazione (pre-calcolate in base al
modello teorico)
2)
on-line: decomposto il fronte d’onda nei coefficienti
di aberrazione, si effettua il calcolo delle forze da
applicare per ognuno degli attuatori
Tecnologie Astronomiche
M. Brescia
ottica attiva con M1 - 2
Tuttavia, per le aberrazioni correggibili mediante M1, il modo analitico migliore per
rappresentarle e quantificarle, sarebbe utilizzare i modi di vibrazione naturale dello specchio,
detti modi elastici. La loro rappresentazione analitica risulta molto più complessa rispetto a
Zernike, ma hanno una maggior precisione di rappresentazione delle aberrazioni di M1 (sferica,
astigmatismo, tricoma etc….), che si riflette su una minore richiesta di forza da applicare agli
attuatori contro-deformanti (risparmio di energia e maggiore sicurezza del sistema rispetto allo
specchio). Nella pratica, Zernike è più preciso per le aberrazioni corrette da M2 (defocus, coma,
tilt), mentre i modi elastici lo sono per le aberrazioni relative ad M1.
Tecnologie Astronomiche
M. Brescia
ottica attiva con M1 - 3
Sia i coefficienti di Zernike che i modi elastici sono insiemi di funzioni mutuamente ortogonali.
Tale ortogonalità si perde in modo trascurabile se si mescolano nel sistema di correzione attiva di
un telescopio. La forma radiale dei modi elastici è molto simile a quella di Zernike. La seguente
tabella mostra la tipica classificazione dei modi elastici e la corrispondente interpretazione in
termini dei coefficienti di Zernike.
Symmetry Order Optical interpretation
0
2
Similar to Spherical 3rd order
0
3
Similar to Spherical 5th order
1
2
Similar to Coma 5th order
2
1
Similar to Astigmatism 3rd order
2
2
Similar to Astigmatism 5th order
3
1
Similar to Tricoma
4
1
Similar to Quadratic Astigmatism
Tecnologie Astronomiche
M. Brescia
ottica attiva con M1 - 4
aberrazioni rotazionalmente simmetriche
Sono corrette applicando un “letto” di forze sugli attuatori laddove non sia importante l’angolo di
incidenza del supporto inferiore dello specchio. Considerato l’anello di attuatori generico R, per
correggere il generico coefficiente di aberrazione m, si ha:
f a , R   M a ,WS Fa , R
Fa , R è la forza di calibrazione per l'aberrazione a relativa all'anello R
M a ,WS è il modulo dell'aberrazione a misurato dal sensore
aberrazioni non rotazionalmente simmetriche
Sono corrette applicando un “letto” di forze dove vi sia dipendenza tra l’anello e l’angolo del
supporto. La forza per l’attuatore i-esimo dell’anello R per l’aberrazione a con ordine di
simmetria o, è la seguente:
f a , R ,i   M a ,WS Fa , R cos  n i   a ,WS ,M 1 
 i è l'angolo del supporto i-esimo
 a ,WS ,M 1 è l'angolo dell'aberrazione (nel sistema M1)
Tecnologie Astronomiche
ottica attiva con M1 - 5
M. Brescia