Nessun titolo diapositiva

Moti relativi
Nel trattare i moti bisogna definire il sistema di riferimento (SR)
rispetto a cui si descrive il moto.
A volte è più semplice usare un SR particolare (in moto rispetto ad
un altro) ed è quindi opportuno poter passare dalla descrizione
in un SR a quella di un altro SR.
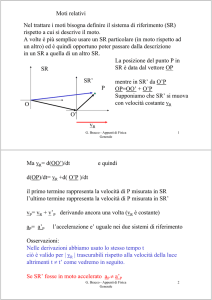
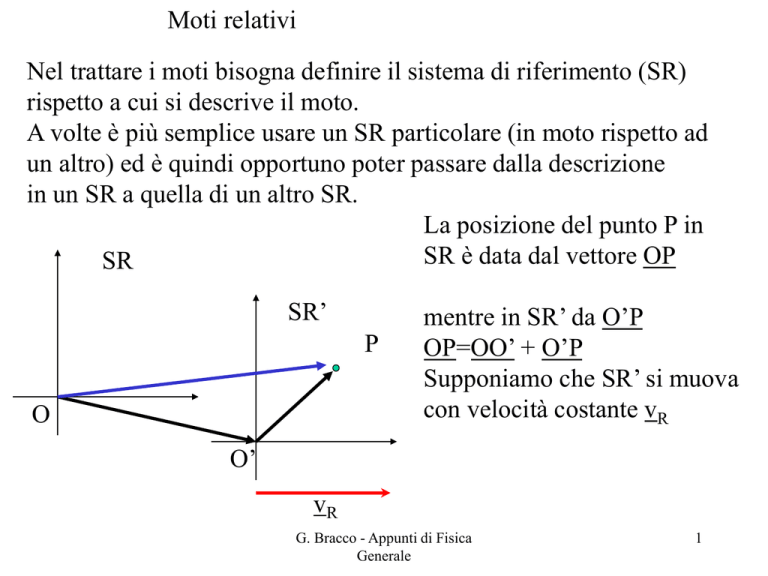
La posizione del punto P in
SR è data dal vettore OP
SR
SR’
P
O
mentre in SR’ da O’P
OP=OO’ + O’P
Supponiamo che SR’ si muova
con velocità costante vR
O’
vR
G. Bracco - Appunti di Fisica
Generale
1
Ma vR= d(OO’)/dt
e quindi
d(OP)/dt= vR +d( O’P )/dt
il primo termine rappresenta la velocità di P misurata in SR
l’ultimo termine rappresenta la velocità di P misurata in SR’
vP= vR + v’P derivando ancora una volta (vR è costante)
aP= a’P
l’accelerazione e’ uguale nei due sistemi di riferimento
Osservazioni:
Nelle derivazioni abbiamo usato lo stesso tempo t
ciò è valido per | vR | trascurabili rispetto alla velocità della luce
altrimenti t  t’ come vedremo in seguito.
Se SR’ fosse in moto accelerato aP  a’P
G. Bracco - Appunti di Fisica
Generale
2
Queste relazioni sono alla base delle Trasformazioni di Galileo
Equazioni di trasformazione di Galileo (V = vR costante)
r=r’ + V t’
t=t’
V con velocità (di trascinamento)
di SR’ rispetto a SR
La trasformazione inversa è data da
r’=r - V t con lo scambio di V in -V
t’=t
Come si vede queste corrispondono a trasformazioni del
sistema di riferimento per traslazione della quantità V t’.
G. Bracco - Appunti di Fisica
Generale
3
I sistemi di riferimento che si muovono di moto rettilineo
uniforme rispetto agli altri hanno un ruolo particolare
e vengono detti Sistemi inerziali
In essi vale il principio di inerzia: Se un corpo non è soggetto
ad azioni esterne mantiene inalterato il suo stato di quiete o di
moto (cioè la sua velocità non cambia).
Se un corpo non accelera in un sistema di riferimento
e se anche in un secondo sistema si misura accelerazione nulla
allora i sistemi devono essere in moto rettilineo uniforme uno
rispetto all’altro. Quindi i due sistemi sono inerziali. Il principio di
inerzia serve perciò a definire quali sono i sistemi inerziali.
G. Bracco - Appunti di Fisica
Generale
4
Azioni su un corpo
Un corpo può modificare il suo stato di moto se vi è un’azione
esterna che chiameremo forza F
Newton collegò fra loro accelerazione di un corpo e forze
(da questo la necessità di definire solo le quantità cinematiche
posizione, spostamento, velocità e accelerazione)
L’accelerazione impressa ad un corpo è direttamente proporzionale
alla forza applicata al corpo (secondo Principio della Dinamica)
a  F (unità: newton, N)
Questa relazione richiede perciò una costante di proporzionalità
che chiameremo massa m (unità: chilogrammo, kg).
F=ma
[F]=MLT-2
secondo Principio della Dinamica (valido in SR inerziale)
{F}=kg m s -2 =N
G. Bracco - Appunti di Fisica
Generale
5
La massa viene anche indicata con la quantità di materia
posseduta da un corpo.
A questo riguardo è opportuno definire la massa volumica
(o densità)  di un corpo che è una caratteristica del materiale
che costituisce un corpo di volume V
m
 = ------ (unità kg/m3)
V
 dipende dalle condizioni ambientali in cui si trova il corpo
(pressione, temperatura). A parità di esse, risulta uguale per
ogni corpo omogeneo costituito dallo stesso materiale.
Per un corpo di spessore trascurabile si può definire la densità
superficiale = m/A (unità kg/m2) A=area del corpo, mentre per uno
filiforme la densità lineare =m/l (unità kg/m)
G. Bracco - Appunti di Fisica
Generale
6
G. Bracco - Appunti di Fisica
Generale
7
Azioni fra corpi diversi
Stabilito che ogni azione corrisponde ad una forza, quando
due corpi A e B interagiscono fra loro ci si può chiedere se solo
B agisce su A od anche A risponde agendo con una forza su B.
Newton trovò che esiste reciprocità ed enunciò il terzo principio
Ad ogni azione corrisponde una reazione uguale e contraria
quindi detta FB la forza che B applica ad A ed FA la forza che
A applica su B, si può affermare che
FA = -FB (ricordarsi che sono applicate a corpi differenti!)
e hanno direzione comune (forze centrali)
FB
FA
G. Bracco - Appunti di Fisica
Generale
8
Tutta la meccanica classica discende da questi principi.
Riassumiamoli perciò nei sistemi inerziali:
1) F=0  v= cost (Primo Principio, Principio di inerzia)
2) F 0  F= ma
3) FAB= -FBA
(Secondo principio della Dinamica)
(Terzo Principio, Principio di azione e reazione)
Questi principi vengono anche chiamati leggi di Newton anche se
il nome principio indica che tali relazioni sono frutto dell’esperienza,
non dimostrabili da altre relazioni e sono il fondamento su cui si basa tutta
la teoria della Meccanica Classica (corpi di dimensioni superiori
a quelle atomiche e che si muovono a velocità piccole rispetto a quella
della luce).
G. Bracco - Appunti di Fisica
Generale
9
E’ da osservare che se su un corpo agiscono più forze, la
seconda legge di Newton va modificata considerando la
somma di tutte le forze (risultante delle forze) F
F=F1+ F2 +…+ Fn =jFj=ma
F3
F1
F2
F1
Ciò esprime il principio
di sovrapposizione delle
forze che discende dalla
loro natura vettoriale.
Quando si scriveranno
leggi che discendono dalla
seconda legge di Newton si
F4
intenderà sempre la forza
risultante anche se non
esplicitamente detto.
G. Bracco - Appunti di Fisica
Generale
10
Torniamo al nostro esempio
at
a
ar
x= (-0.31 t2+ 7.2 t+28) m
y= (0.22 t2 - 9.1 t+30) m
e calcoliamo la forza a cui è soggetto
un corpo che segue quella traiettoria
di m=2.0 kg.
da F=ma
occorre conoscere l’accelerazione
a=(-0.62,0.44) m/s2
e quindi F=(-1.24,0.88) N
E’ la sola forza applicata?
G. Bracco - Appunti di Fisica
Generale
11
Sistemi di riferimento non inerziali
Le leggi di Newton valgono in riferimenti inerziali.
Nei riferimenti non inerziali, il moto del riferimento introduce
delle forze fittizie. Infatti prendiamo il caso di un riferimento SR’
che accelera rispetto a quello inerziale SR e ripetiamo il calcolo
OP=OO’ + O’P deriviamo
rispetto al tempo
SR
SR’
vP= vR + v’P derivando ancora
P
O
O’
aP= aR + a’P con aR
l’accelerazione di SR’ rispetto
a SR
aR
G. Bracco - Appunti di Fisica
Generale
12
Ma se ad ogni accelerazione corrisponde ad una forza per il corpo P
scriveremo
nel sistema SR: F=ma
nel sistema SR’: F’= ma’
ma da
ma= maR + ma’
F- maR = ma’
quindi l’accelerazione del sistema SR’ viene vista come
una forza - maR che non risulta legata all’azione di nessun corpo
ma che agisce su tutti i corpi considerati da SR’.
Es. autobus che accelera, tutti i passeggeri sono spinti verso la
parte posteriore.
G. Bracco - Appunti di Fisica
Generale
13
Si osservano forze fittizie (dette anche inerziali o pseudoforze) anche
nel caso di un sistema rotante, sebbene la trattazione sia più complicata.
Abbiamo già visto che un corpo che ruota di moto circolare uniforme
ha una accelerazione centripeta |a| = 2r’ = v2 /r’ dovuta ad una forza
che causa il moto circolare (es. fune vincolata ad una estremità,
che trattiene il corpo)
Supponiamo che il corpo A di massa m sia su una giostra che ruota alla
stessa velocità angolare = |v|/r’ . Rispetto alla giostra il corpo A è fermo
e quindi a’=0 (e v’=0). Ma la forza centripeta della fune è reale e quindi
causerebbe il movimento verso il centro di rotazione. Occorre che
vi sia una forza centrifuga (fittizia) che equilibri la forza reale.
Es. autobus in curva: i passeggeri in piedi devono tenersi alle
maniglie per non scontrare le pareti laterali.
G. Bracco - Appunti di Fisica
Generale
14
Per un sistema rotante, oltre alla forza centrifuga ci sono anche
altre forze fittizie legate
1) alla variazione della velocità angolare nel tempo
(accelerazione angolare =d/dt forza corrispondente m r’ )
2) al moto del corpo rispetto al sistema rotante
(forza di Coriolis m (2 v’) )
Nel caso della Terra la forza di Coriolis determina uno spostamento
nel moto di masse d’aria (vento) o d’acqua (correnti),
l’erosione prevalente di una sponda dei fiumi rispetto all’altra,
il consumo prevalente di una rotaia dei treni rispetto all’altra, ….
Questi effetti dipendono dalla posizione (emisfero boreale o australe)
sulla superficie della Terra.
Animazione: inerziali (par)
G. Bracco - Appunti di Fisica
Generale
15
Sistema
non
inerziale
Sistema
inerziale
G. Bracco - Appunti di Fisica
Generale
16
In questo esempio una
pallina si muove sopra
un disco che ruota (non
c’e’ contatto tra pallina
e disco). Nel sistema
inerziale la traiettoria
della pallina è rettilinea
e la risultante delle
forze applicate è nulla.
Nel sistema non
inerziale (fisso con il
disco) la traiettoria è
curva a causa del moto
del disco e occorre
introdurre una risultante
diversa da zero.
G. Bracco - Appunti di Fisica
Generale
17
Cenni alla Relatività ristretta
Se la velocità relativa dei due SR è elevata le trasformazioni di Galileo devono
essere sostituite da quelle di Lorentz. La necessità di tali trasformazioni è dovuta al
fatto che la velocità della luce “c” è risultata sempre costante nonostante vari
esperimenti siano stati fatti per confutarne la costanza.
Se una sorgente in moto a velocità v emette un impulso di luce, la luce viaggia a
velocità c e non c+v come vorrebbero le trasformazioni di Galileo.
Einstein nel 1905 partì dalle seguenti 2 ipotesi:
1)(principio di relatività) le leggi della fisica sono uguali in tutti i sistemi di
riferimento inerziali
2)la velocità della luce nel vuoto è una costante uguale per tutti i sistemi di
riferimento.
Il principio di relatività estende quello insito nelle trasformazioni di Galileo che
richiedeva che le leggi (solo) della meccanica fossero uguali per tutti gli
osservatori inerziali poiché l’accelerazione è la stessa (F=ma). Tutto ciò si basa sul
concetto di spazio e tempo assoluti e tale concetto verrà profondamente
modificato: lo spazio e il tempo non sono più da considerarsi entità separate.
Einstein mostrò che la simultaneità degli eventi è relativa al SR. Infatti per definire
la simultaneità, ovvero che due eventi avvengano nello stesso istante, bisogna
definire una procedura.
G. Bracco - Appunti di Fisica
18
Generale
Per definire che due eventi che avvengono in P e Q siano simultanei,
quando capitano mandiamo due impulsi di luce verso il punto medio M
di PQ. Se i due impulsi arrivano nello stesso istante, gli eventi sono
Consideriamo ora due sperimentatori, uno
simultanei.
fermo, SF, e uno, SM, in moto relativo con
velocità v. Presa la stessa base spaziale da
SF (AC con punto medio B) e da SM (LN
M
P
Q
con punto medio M),
ACLN, poniamo in B e M due sorgenti di luce che emettono impulsi
verso A,B e L,N rispettivamente. Quando M passa per B vengono
emessi queste coppie di impulsi. SF vede arrivare
contemporaneamente gli impulsi in A e C.
C
A
B
Parimenti SM vede arrivare contemporaneamente
in L e N gli impulsi. Questa descrizione
N però non è quella vista da SF. Infatti il punto N si
L
M
allontana dal punto di partenza, cioè quando MB e ci fu l’emissione
dell’impulso sia per SF sia per SM, al contrario L si avvicina.
G. Bracco - Appunti di Fisica
Generale
19
Quindi l’impulso arriva prima in L che in A e
arriva dopo in N rispetto a C. La
B
contemporaneità è perciò un concetto relativo.
C
A
1
2
Per SF, xL(t)=xL(0)+vt, xN(t)=xN(0)+vt
Ed i 2 impulsi x1(t)=xM(0)-ct, x2(t)=xM(0)+ct
M
L
N Arrivano in L e N ai tempi determinati da
x1(t1)=xL(t1) , x2(t2)=xN(t2). Se d è la distanza fra L e N, si ha perciò
t1=(xM(0)- xL(0))/(c+v)=d/(2(c+v)), t2=(xN(0)- xM(0))/(c-v)=d/(2(c-v))
e SF vede i due eventi non contemporanei ma separati da un intervallo
t=t2- t1=v d/(c2-v2). Le coordinate spaziali dei punti L e N per SF
sono x1= x1(t1)=xM(0)-ct1, x2=x2(t2)=xM(0)+ct2, ovvero x=x2- x1=c(t2+
t1)=c2 d/(c2-v2) e, confrontandola con l’espressione per i tempi, t=(v/
c2 ) x. Solo se la velocità della luce c, gli eventi, che capitano in
punti diversi per SF, sarebbero contemporanei. Questo mostra che se c
è finita e uguale per tutti gli osservatori inerziali, tempo e spazio non
possono essere più considerati separati ma si devono considerare come
componenti di un vettore quadridimensionale (x,y,z,ct).
x
G. Bracco - Appunti di Fisica
Generale
20
È possibile dimostrare che le trasformazioni di Lorentz (la direzione
del moto relativo è presa come asse x per entrambi i sistemi S e S’,
quest’ultimo si muove con velocità v rispetto a S) sono espresse da:
x’=(x-vt), y’=y, z’=z, t’=[t-(v/c2)x],
e quelle inverse (v diventa –v)
x=(x’+vt’), y=y’, z=z’, t=[t’+(v/c2)x’]
da osservare che il tempo non e’ lo stesso ma si trasforma in modo
simile alla coordinata spaziale x, il coefficiente di Lorentz vale
=(1-v2 /c2)-½ e per v<<c tende a 1 e quindi x’=x-vt e t’=t cioè le
trasf.di Lorentz tendono a quelle di Galileo per velocità piccole in
confronto a c. Le trasformazioni per la velocità sono
vx’= (vx-v)/(1- vxv/c2), vy’= (vy/ )/(1- vxv/c2), vz’= (vz/ )/(1- vxv/c2)
e quelle inverse
vx= (v’x+v)/(1+ vxv/c2), vy= (v’y/ )/(1+ vxv/c2), vz= (v’z/ )/(1- vxv/c2),
Da osservare che la somma di velocità è sempre inferiore o uguale a c
come richiede il risultato sperimentale.
G. Bracco - Appunti di Fisica
Generale
21
L’accelerazione non è più un invariante come per le trasf.di Galileo ma
ax’= ax/ [(1- vxv/c2)]3, ay’= ay/ [(1- vxv/c2)]2+(axv vy /c2)/[2(1- vxv/c2)3]
, az’= az/ [(1- vxv/c2)]2+(axv vz /c2)/[2(1- vxv/c2)3] .
In conclusione, osserviamo ancora che:
si hanno effetti di dilatazione temporale (nel sistema in moto, il tempo
scorre più lentamente)
di contrazione spaziale (nella direzione delle velocità v tra i sistemi di
riferimento le lunghezze sono accorciate, perpendicolarmente al moto
non si ha variazione).
La massa di un corpo non è più un invariante ma dipende dallo stato di
moto del corpo stesso. Infatti se rimanesse costante, applicando una forza
costante si ottiene un’accelerazione costante e quindi basta aspettare un
tempo finito per raggiungere la velocità c e superarla. Invece m= m0,
dove m0 è la massa a riposo (per i fotoni che viaggiano a velocità c, la
massa è nulla!). Da questo si ricava anche che la massa di un corpo può
essere trasformata in energia (quantità che definiremo in seguito) e
viceversa con la ben nota G. Bracco - Appunti di Fisica relazione E=m0c2. 22
Generale
Scrittura in termini matriciali della trasformazione di Lorentz
x’=(x-vt), y’=y, z’=z, t’=[t-(v/c2)x],
x’  
| y’ |= | 0
| z’ | | 0
t’  -(v/c2)
0
1
0
0
0 -v  x 
0 0 ||y|
1 0 ||z |
0  t
corrisponde ad una rotazione nello spazio quadridimensionale che
anziché conservare la distanza (euclidea) in 3D come le rotazioni già
incontrate, conserva la velocità della luce c o meglio l’intervallo
percorso dalla luce nel tempo t in qualunque sistema di riferimento
x2+ y2+ z2=(ct)2 , x2+ y2+ z2-(ct)2=0 ed anche x’2+ y’2+ z’2-(ct’)2=0 .
G. Bracco - Appunti di Fisica
Generale
23